NBER:新冠的感染率估计 | 唧唧堂论文解析
picture from Internet
专栏介绍
![]()
长按二维码直接进入专栏
本文为唧唧堂《新冠病毒主题论文导读专栏》内一篇论文解析,唧唧堂将在本专栏收录发布所有新冠病毒主题的经济金融社会心理等社科类论文解析导读,同时也或将收录部分医学论文。
本专栏论文收录无截止时限,现已有超100篇NBER工作论文解析中,未来唧唧堂将源源不断把发现的新冠病毒主题论文放入本专栏,期待各位研究人的关注与订阅。点击了解专栏!
唧唧堂现招募更多经济金融研究人加入写作小组,以更快完成本专栏内容的解析产出。点击加入写作小组!
本文是针对《COVID-19感染率估计》(NBER Estimating the COVID-19 Infection Rate:Anatomy of an Inference Problem)的论文解析, 文章为美国国家经济研究局(NBER) 4月的工作论文。作者分别是Charles F.Manski(美国西北大学)和Francesca Molinari(康奈尔大学)。
文章摘要:由于新冠病毒的检验数据不全以及检验的不准确性,现阶段报告的新冠病毒的人口感染率应该比实际的感染率要低,因此,在确诊病例中确定的危重病例比例会高于实际的比例。更好地估计感染率的值域范围有利于更好地了解COVID-19传播的时间路径。本文提供了如何估算感染率值域的方法,在根据现实情况对未检测的人口的感染率和现存检测的准确性进行了可信假设的基础上,使用来自美国伊利诺伊州、纽约州和意大利三个地方的数据,估算了COVID-19传染率的在这三个地方的值域范围(而不是仅提供一个点估计值)。本文发现现在的感染率可能远高于报告的感染率,同时意大利确诊案例中的实际致死率应该远低于报告的结果。
介绍
想要准确衡量COVID-19这类的传染病传播的时间路径,比较全面的数据必不可少,数据不全一直是研究的重要困难之一。一般来说,确诊的案例只能衡量参与了检测的人口中的阳性检验数量,而无法衡量未参与检测的人口中有多少人受到感染。另一方面,参与检测的人口往往与不参与检测的人口具有显著区别,参与检测的人群要么是已经出现了感染病的典型症状,要么是曾经近距离地接触过确诊的病例,在不参与检测的人群中可能有很多无症状COVID-19感染者,这些感染者并未计入统计中,所以真实的感染率可能要高于现在统计得到的感染率。
在研究传染病的时候,另一个潜在问题是确诊手段的可信性。检测时确诊的准确率具有不对称性,很多研究表明,对于传染病的检测,阳性预测值(得到阳性检测结果的人确实受到了感染的概率)一般接近于1,而阴形预测值(得到阴性检测结果的人确实没有被感染的概率)一般显著小于1,在这样的不对称性下,统计得到的感染率可能会被进一步低估。
综合上述两条原因,本文认为实际的感染率应该大于统计报告的感染率。感染病例中危重病例比例的计算公式为危重病例(确诊病例中住院、接受重症治疗或死亡的病例)比例除以感染率,假设危重病例的衡量相对准确,即该公式中的分子相对准确,那么统计报告中低估的感染率会使计算公式的分母部分被过度低估,从而高估危重病例比例。
2020年3月3日,世界卫生组织发表声明称COVID-19确诊病例死亡率约为3.4%,这个数值由于上述的各种原因,应该被当作COVID-19的确诊死亡率的上限值,而不应该被当作一个可信的点估计或平均值。许多学者意识到了这个问题,并且提出为了更好地衡量COVID-19的感染率和死亡率,我们应该对人口进行随机抽样调查以解决数据不全的问题。在现阶段无法进行随机抽样的情况下,很多研究尝试使用不同的假设对传染率和危重病例比例进行估计与预测,但是,不同的假设往往会给出非常不同的结果(点估计结果),现阶段,由于我们缺乏对现实情况的了解,学界无法合理判断哪些假设是可信的,因此,也就很难判断哪个点估计结果是更有价值的。
在这样的背景下,本文提出了一个新的思路,与其执着于选择一个可信的假设条件从而获得一个可信的点估计结果,本文作者在多重假设的前提下,估计了COVID-19的感染率和危重病例比例的值域空间。对重要比率进行值域估计的研究方法有时候也被称为敏感性分析,它的优势在于不需要选择太多过强的假设条件,其结果可能更贴近现实情况。另外,本文使用了计量经济学中“部分识别”的研究方法,在弱假设条件下只给出结果的集合点估计,而不是某一个单一的数值点估计。该方法的技术细节可参见论文(Manski, 1995,2003,2007;Tamer,2010; Molinari,2020)。
在估计COVID-19的感染率值域时,现阶段的数据和可信假设使感染率的值域下限较易得到,比较难得到的是该值域的上限。本文解释了我们识别时遇到的逻辑问题、选择和使用的可信假设,以及估计出的集合数值。
本文使用的数据来自美国伊利诺伊州、纽约州和意大利,时间跨度为2020年3月16日至4月6日,我们的估计结果为:美国伊利诺伊州、纽约州和意大利的感染率值域分别是:[0.001, 0.517], [0.008, 0.645],[0.003, 0.510]。危重病例比例的值域为:[0.001, 0.172], [0, 0.02], 和[0.001, 0.086]。
方法
本文首先使用一个较为抽象的模型,对感染率的概率条件进行分解,逐步增加可信假设以估算感染率的值域范围,在感染率的值域基础上估算危重病例比例的值域范围。接着,我们使用可观测的病人特质对这两个概率进行进一步的定义与估算,希望这些结果会对公共健康政策的制定有所帮助。
估计人口感染率的值域
对于某一特定人群(这个人群可以是一个城市、一个州或者一个国家的全部人口),我们的目标是研究截止至某一个特定日期d,该人群中感染COVID-19病毒的比例为多少。
我们假设一个人最多感染该病毒一次,如果一个人感染了病毒,那么他只有两种结局:要么康复后获得了免疫,要么是死亡。康复后获得对该病毒的免疫是一个比较合理的假设,在现阶段看来,至少在康复后的一段时期内,这种免疫是存在的。我们还假设该研究人群的人口总数不变,也就是说,我们暂时不考虑由于COVID-19和其他原因造成的死亡会减少总人口的情况,也不考虑出生和移民移入会增加总人口的情况。
让C_d=1代表一个人在日期d感染了病毒,P(C_d=1)代表截止至日期d,一个人感染病毒的概率,它也同时代表着一个人群截止至日期d的病毒感染率,P(C_d=1)无法直接观测到。与P(C_d=1)相关的两个变量,人群中接受检测的比例和接受检测人中得到阳性结果的比例,是可观测的数据。为了简化后续的分析,我们假设一个人在日期d之前最多被检测一次。
让T_d=1代表一个人在日期d之前接受了检测,R_d=1代表一个人获得了阳性的检测结果,那么我们可以得出以下结论:T_d=0(没接收检测) 可推导出 R_d=0(没有得到阳性结果);R_d=1(得到阳性结果) 可推导出T_d=1(接受了检测)。根据全概率公式,我们可以把感染率分解如下:
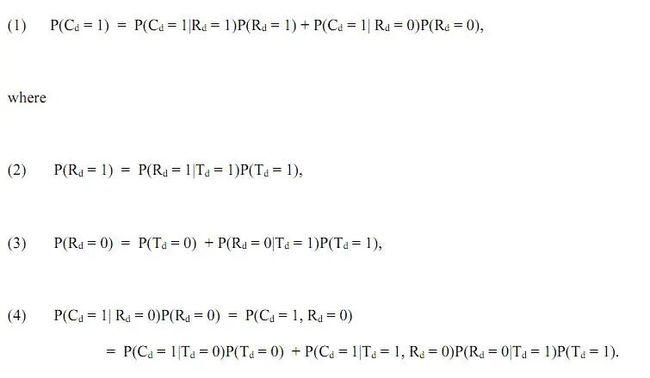
(1) P(感染) = P(感染 | 阳性结果)P(阳性结果) + P(感染 | 非阳性结果)P(非阳性结果)
(2)P(阳性结果) = P(阳性结果 | 接受检测)P(接受检测)
(3)P(非阳性结果) = P(未接受检测) + P(非阳性结果 | 接受检测)P(接受检测)
(4)P(感染 | 非阳性结果)P(非阳性结果) = P(感染,非阳性结果) = P(感染 | 未接受检测)P(未接受检测) + P(感染 | 接受检测,非阳性结果)P(非阳性结果 | 接受检测)P(接受检测)
假设检测报告是准确的,接受检测率和已测中阳性结果的比率已知,那么P(未接受检测),P(接受检测),P(非阳性结果 | 接受检测)和P(阳性结果 | 接受检测)可以被观测到,其他的概率无法直接观测到。
P(感染 | 阳性结果)和P(感染 | 非阳性结果)的数值由检测的准确性决定。P(感染 | 阳性结果)对应阳性预测值,P(感染 | 非阳性结果)对应1-阴性预测值。医学界在定义检测的准确性时并不是用这两个指标,而更多地使用敏感性和特异性来衡量检测的准确度。其中,敏感性=P(阳性结果 | 接受检测,感染),特异性=P(非阳性结果 | 接受检测,未感染)。根据贝叶斯全概率公式,敏感性/特异性与阳性/阴性预测值之间的关系可以被推导出来,其中,在P(感染 | 接受检测)>0的情况下,阳性预测值=1与特异性为1为充分必要条件。
医学界当前的研究表明,COVID-19的特异性接近1,也就是说阳性预测值,P(感染 | 阳性结果)可以被假设为1。COVID-19的阴性预测值存在争议,一些医学研究者认为COVID-19的假阴性概率至少是0.3。有些研究认为COVID-19的检测与之前的流感检测有相似性,根据Peci与合著者(2014)的研究,流感的阳性预测值为0.995,阴性预测值为0.853。除此之外,由于COVID可能存在变异性,随着时间的变化和接受检测人群的结构变化,阴性预测率也可能会发生较大的改变。因此,本文假设阴性预测率在[0.6,0.9]之间,对应的是,P(感染 | 接受检测,非阳性结果)大概在[0.1,0.4]。
P(感染 | 未接受检测)的值域与感染率的值域估计具有很大关联。未接受检测的人群中感染病毒的比例存在许多不确定性,本文将对该概率进行数据模拟,通过代入不同的数值来估计真实感染率的值域。
综上,感染率P(感染)的值域可以表达如下:
让[L_d0,U_d0]代表P(感染 | 未接受检测)的可信值域区间,[L_d10,U_d10]代表P(感染 | 接受检测,非阳性结果)的可信值域区间,假设P(感染 | 阳性结果)=1,公式(1)可以被表示为:
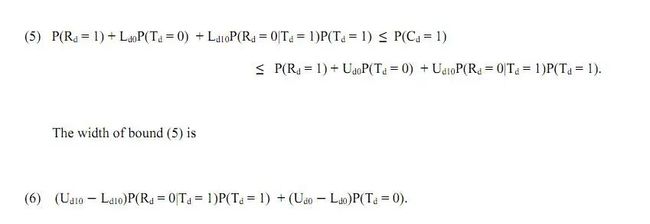
(5) P(阳性结果) + L_d0*P(未接受检测) + L_d10*P(非阳性结果 | 接受检验)P(接受检验) <= P(感染) <=P(阳性结果) + U_d0*P(未接受检测) + U_d10*P(非阳性结果 | 接受检验)P(接受检验)
值域范围为:
(6) (U_d0 -L_d0)*P(未接受检测) + (U_d10 - L_d10)*P(非阳性结果 | 接受检验)P(接受检验)
从公式(6)可以看出,感染率的值域取决于两方面的不确定性:1)检测的准确性(U_d0 - L_d0);2)未接收检测人群的感染率(U_d10 - L_d10)。P(接受检测)与 P(未接受检测)可以被看作是上述两个不确定性的线性加权。
