C实现二叉树(模块化集成,遍历的递归与非递归实现)
C实现二叉树模块化集成
实验源码介绍(源代码的总体介绍):
header.h : 头文件链栈,循环队列,二叉树的结构声明和相关函数的声明。
LinkStack.c : 链栈的相关操作函数定义。
Queue.c : 循环队列的相关操作函数定义。
BinTree.c : 二叉树的相关操作的函数定义,层序序列生成二叉树,二叉树的前序序列、中序序列、后序序列的递归和非递归实现,求叶子结点的递归与非递归实现,求树高。
由于我还是学生(初学者)且第一次写类似的博客,文章中难免会有错误!如发现错误,望各路大神能够指出!
详见源代码!
源代码:header.h

/** * header.h */ /** * BinTree */ typedef int BinTree_Type; typedef struct TreeNode BinTree; struct TreeNode { BinTree_Type Data; BinTree *Left; BinTree *Right; }; /** * Queue */ #define MaxSize 50 typedef BinTree * Q_ElementType; typedef struct { Q_ElementType Data[MaxSize]; int front; int rear; } Queue; extern Queue * InitQueue(); extern void Destory(Queue * q); extern int IsQueueEmpty(Queue *q); extern void EnQueue(Queue *q, Q_ElementType e); extern Q_ElementType DeQueue(Queue* q); /** * LinkStack */ typedef BinTree * L_ElementType; typedef struct Node { L_ElementType Data; struct Node *next; } LinkStack; extern LinkStack * InitStack(); extern int IsStackEmpty(LinkStack *s); extern void Push(LinkStack *s, L_ElementType e); extern L_ElementType Pop(LinkStack *s); extern L_ElementType getTop(LinkStack *s);
源代码:LinkStack.c

#include <stdio.h> //standard input output 标准输入输出头文件 #include <malloc.h> //memory allocation分配 #include "header.h" /** * 初始化一个头结点为空的Stack * init a stack with a NULL head */ LinkStack * InitStack() { LinkStack *s = (LinkStack *) malloc(sizeof(LinkStack)); s->next = NULL; return s; } /** * 若stack为空返回1,否则返回0 */ int IsStackEmpty(LinkStack *s) { return s->next == NULL; } /** * 入栈 */ void Push(LinkStack *s, L_ElementType e) { struct Node *p; p = (LinkStack *) malloc(sizeof(LinkStack)); p->Data = e; p->next = s->next; s->next = p; } /** * 出栈 */ L_ElementType Pop(LinkStack *s) { if (s->next == NULL) { printf("Stack is NULL"); return NULL; } L_ElementType TopElem; struct Node *top; top = s->next; s->next = top->next; TopElem = top->Data; free(top); return TopElem; } /** * 返回栈顶元素 */ L_ElementType getTop(LinkStack *s) { if (s->next == NULL) { printf("Stack is NULL"); return NULL; } return s->next->Data; }
源代码:Queue.c

#include <stdio.h> #include <malloc.h> #include "header.h" /** * 初始化循环队列 */ Queue * InitQueue() { Queue *q = (Queue *) malloc(sizeof(Queue)); q->front = q->rear = 0; return q; } /** * 销毁队列 */ void Destory(Queue * q) { free(q); } /** * 判断队列是否为空 */ int IsQueueEmpty(Queue *q) { return q->front == q->rear; } /** * 入队 */ void EnQueue(Queue *q, Q_ElementType e) { if ((q->rear + 1) % MaxSize == q->front) { printf("队列满了"); return; } q->rear = (q->rear + 1) % MaxSize; q->Data[q->rear] = e; } /** * 出队 */ Q_ElementType DeQueue(Queue* q) { if (q->front == q->rear) { printf("队列空了!"); return NULL; } q->front = (q->front + 1) % MaxSize; return q->Data[q->front]; }
源代码:BinTree.c
#include <stdio.h> #include <malloc.h> #include "header.h" /** * 访问 */ void Visited(BinTree *BT) { printf("%d ", BT->Data); } /** * 层序生成二叉树 */ BinTree *CreateBinTree() { BinTree_Type Data; BinTree *BT = NULL, *T = NULL; Queue * Q = NULL; Q = InitQueue(); /* 生成一个队列 */ scanf("%d", &Data); /* 建立第一个结点,即根节点 */ if (Data) { /* 分配结点单元,并将结点地址入队 */ BT = (BinTree *) malloc(sizeof(BinTree)); BT->Data = Data; EnQueue(Q, BT); } else { return NULL; /* 若第一个数据就是0,则返回空树 */ } while (!IsQueueEmpty(Q)) { T = DeQueue(Q); /* 从队列中取出一结点地址 */ scanf("%d", &Data); /* 读入T的左孩子 */ if (Data) { /* 分配新结点,作为出对结点左孩子 */ T->Left = (BinTree *) malloc(sizeof(BinTree)); T->Left->Data = Data; EnQueue(Q, T->Left); /* 新结点入队 */ } else { T->Left = NULL; } scanf("%d", &Data); /* 读入T的右孩子 */ if (Data) { /* 分配新结点,作为出对结点右孩子 */ T->Right = (BinTree *) malloc(sizeof(BinTree)); T->Right->Data = Data; EnQueue(Q, T->Right); /* 新结点入队 */ } else { T->Right = NULL; } } /* 结束while */ return BT; } /** * 遍历二叉树 递归算法 */ void PreOrderTraversal(BinTree *BT) { if (BT) { //BT != NULL Visited(BT); PreOrderTraversal(BT->Left); PreOrderTraversal(BT->Right); } } void InOrderTraversal(BinTree *BT) { if (BT) { InOrderTraversal(BT->Left); Visited(BT); InOrderTraversal(BT->Right); } } void PostOrderTraversal(BinTree *BT) { if (BT) { PostOrderTraversal(BT->Left); PostOrderTraversal(BT->Right); Visited(BT); } } /** * 遍历二叉树 非递归算法 */ /** * 前序遍历非递归算法 */ void PreOrderTraversal_Iter(BinTree *BT) { BinTree *T; LinkStack * S = InitStack(); /* 生成一个堆栈 */ T = BT; while (T || !IsStackEmpty(S)) { while (T) { /* 一直向左并访问沿途结点后压入堆栈S */ Visited(T); Push(S, T); T = T->Left; } if (!IsStackEmpty(S)) { T = Pop(S); /* 结点弹出堆栈 */ T = T->Right; /* 转向右子树 */ } } } /** * 中序遍历非递归算法 */ void InOrderTraversal_Iter(BinTree *BT) { BinTree *T; LinkStack * S = InitStack(); /* 生成一个堆栈 */ T = BT; while (T || !IsStackEmpty(S)) { while (T) { /* 一直向左并将沿途结点后压入堆栈S */ Push(S, T); T = T->Left; } if (!IsStackEmpty(S)) { T = Pop(S); /* 结点弹出堆栈 */ Visited(T); T = T->Right; /* 转向右子树 */ } } } /** * 后序遍历非递归算法一 * 此思路来源于数据结构教程(李春葆主编) */ void PostOrderTraversal_Iter1(BinTree *BT) { if (BT == NULL) return; BinTree *p, *T; LinkStack * S = InitStack(); T = BT; int flag = 0; do { while (T) { /* 一直向左并将沿途结点后压入堆栈S */ Push(S, T); T = T->Left; } /* 执行到此处,栈顶元素没有做孩子或左子树均已访问过 */ flag = 1; /* 表示 T的左孩子已访问或为空 */ p = NULL; /* p指向栈顶结点的前一个已访问的结点 */ while (!IsStackEmpty(S) && flag) { T = getTop(S); /* 获取当前的栈顶元素,不是删除 */ /** * 若p=NULL,表示T的右孩子不存在,而左孩子不存在或已经被访问过,所以访问T; * 若p≠NULL,表示T的右孩子已访问(原因是p指向T的右子树中刚访问过的结点,而p是T的右孩子, * p一定是T的右子树中后序序列的最后一个结点),所以可以访问T. */ if (p == T->Right) { Visited(T); /* 访问 */ p = Pop(S); /* 弹出刚访问的结点并将p指向刚访问的结点 */ } else { T = T->Right; /* T指向T的右孩子 */ flag = 0; /* 表示T的右孩子尚未被访问过 */ } } } while (!IsStackEmpty(S)); } /** * 后序遍历非递归算法二 * 思路:要保证根结点在左孩子和右孩子访问之后才能访问,因此对于任一结点p,先将其入栈。 * 如果p不存在左孩子和右孩子,则可以直接访问它; * 或者P存在左孩子或者右孩子,但是其左孩子和右孩子都已被访问过了,则同样可以直接访问该结点。 * 若非上述两种情况,则将P的右孩子和左孩子依次入栈,这样就保证了每次取栈顶元素的时候, * 左孩子在右孩子前面被访问,左孩子和右孩子都在根结点前面被访问。 * (此思路来源于博客园海子!!!) */ void PostOrderTraversal_Iter2(BinTree *BT) { if (!BT) return; BinTree *p, *cur; LinkStack *S = InitStack(); p = NULL; cur = NULL; Push(S, BT); while (!IsStackEmpty(S)) { cur = getTop(S); if ((!cur->Left && !cur->Right) /* NULL==cur->Left && NULL==cur->Right */ || (p && (p == cur->Left || p == cur->Right))) { Visited(cur); p = Pop(S); } else { if (cur->Right) { Push(S, cur->Right); } if (cur->Left) { Push(S, cur->Left); } } } } /** * 层序遍历 */ void LevelOrderTraversal(BinTree *BT) { BinTree *T; T = BT; if (!T) { return; } Queue *Q = InitQueue(); /* 生成一个队列 */ EnQueue(Q, T); /* 根节点入队 */ while (!IsQueueEmpty(Q)) { /* 队列不为空,弹出一个元素 */ T = DeQueue(Q); Visited(T); /* 访问 */ if (T->Left) /* 左子树不为空入队 */ EnQueue(Q, T->Left); if (T->Right) /* 右子树不为空入队 */ EnQueue(Q, T->Right); } } /** * 访问叶子结点的递归算法 */ void getOrderPrintLeaves(BinTree *BT) { if (BT) { if (!BT->Left && !BT->Right) { Visited(BT); } getOrderPrintLeaves(BT->Left); getOrderPrintLeaves(BT->Right); } } /** * 访问叶子结点的非递归算法 */ void getOrderPrintLeaves_Iter(BinTree *BT) { BinTree *T; LinkStack *S = InitStack(); T = BT; while (T || !IsStackEmpty(S)) { while (T) { Push(S, T); T = T->Left; } if (!IsStackEmpty(S)) { T = Pop(S); if (!T->Left && !T->Right) { /* 当该结点的左子树和右子树都为空,访问 */ Visited(T); } T = T->Right; } } } /** * 求树高 */ int PostOrderGetHeight(BinTree *BT) { int LH, RH, MaxH; if (BT) { LH = PostOrderGetHeight(BT->Left); RH = PostOrderGetHeight(BT->Right); MaxH = (LH > RH ? LH : RH); return MaxH + 1; } return 0; }
源代码:Test.c

#include <stdio.h> #include <stdlib.h> #include "header.h" extern BinTree *CreateBinTree(); extern void PreOrderTraversal(BinTree *BT); extern void InOrderTraversal(BinTree *BT); extern void PreOrderTraversal(BinTree *BT); extern void InOrderTraversal(BinTree *BT); extern void PostOrderTraversal(BinTree *BT); extern void PreOrderTraversal_Iter(BinTree *BT); extern void InOrderTraversal_Iter(BinTree *BT); extern void PostOrderTraversal_Iter1(BinTree *BT); extern void PostOrderTraversal_Iter2(BinTree *BT); extern void LevelOrderTraversal(BinTree *BT); extern void getOrderPrintLeaves(BinTree *BT); extern void getOrderPrintLeaves_Iter(BinTree *BT); extern int PostOrderGetHeight(BinTree *BT); int main() { puts("START!!!"); printf("\n层序序列生成二叉树,请输入层序序列(类型为int,0代表为树的位置为NULL):\n"); BinTree * BT = CreateBinTree(); printf("PreOrderTraversal: "); PreOrderTraversal(BT); printf("\n"); printf("InOrderTraversal: "); InOrderTraversal(BT); printf("\n"); printf("PostOrderTraversal: "); PostOrderTraversal(BT); printf("\n"); printf("PreOrderTraversal_Iter: "); PreOrderTraversal_Iter(BT); printf("\n"); printf("InOrderTraversal_Iter: "); InOrderTraversal_Iter(BT); printf("\n"); printf("PostOrderTraversal_Iter1: "); PostOrderTraversal_Iter1(BT); printf("\n"); printf("PostOrderTraversal_Iter2:"); PostOrderTraversal_Iter2(BT); printf("\n"); printf("LevelOrderTraversal: "); LevelOrderTraversal(BT); printf("\n"); printf("getOrderPrintLeaves: "); getOrderPrintLeaves(BT); printf("\n"); printf("getOrderPrintLeaves_Iter: "); getOrderPrintLeaves_Iter(BT); printf("\n"); printf("PostOrderGetHeight: %d",PostOrderGetHeight(BT)); printf("\n"); puts("END!!!"); return EXIT_SUCCESS; }
运行结果:
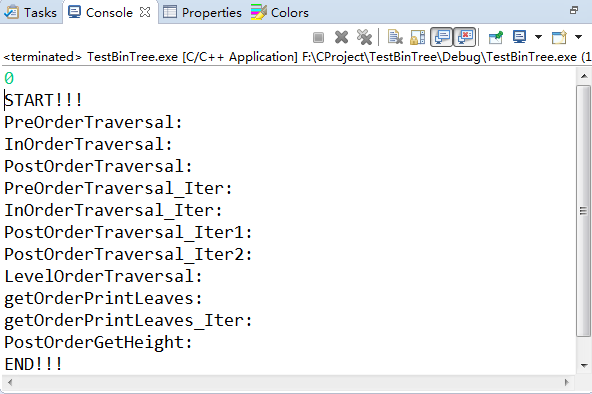
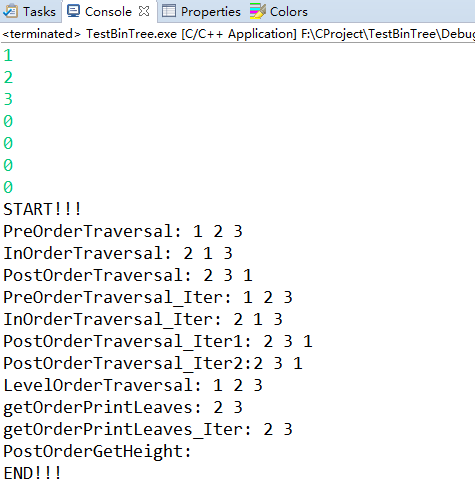
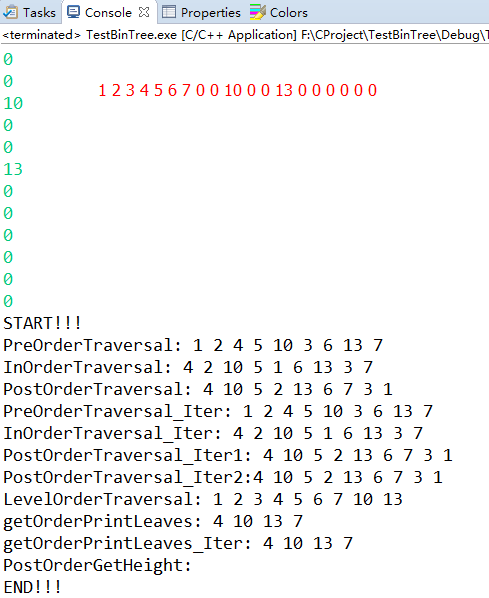
版权声明:本文为博主原创文章,未经博主允许不得转载。
