常见算法技巧之——双指针思想
双指针思想是指设置两个指针解决一些算法问题。一般用的比较多的就是去解决数组、链表类的问题,还有很耳熟能详的二分查找问题。本文将根据自己平时做题的总结以及在网上看到的其他大佬的总结讲解来讨论一下双指针的使用技巧。本文会根据我平时做题实时更新。
快慢指针
双指针的快慢指针用法是我最开始理解的第一种用法。快慢指针一般用来解决链表的问题多一些。设置一快一慢两个指针fast和slow,初始化指向链表表头。
1、计算链表的中点
给定一个链表,要求返回该链表的中点节点。
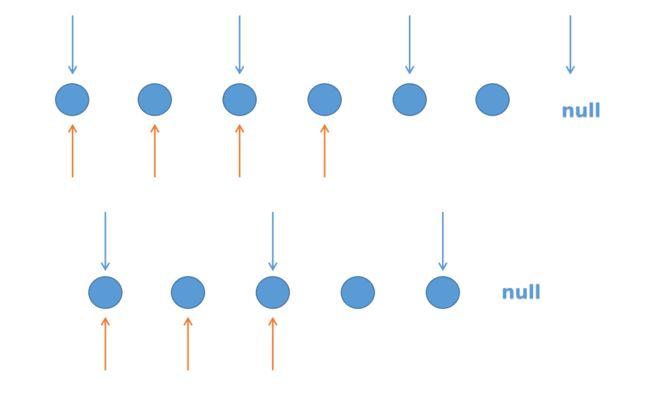
设置两个快慢指针,都从头节点开始,快指针每次前进两个节点,慢指针每次前进一个节点,当快指针到达链表末尾的时候,慢指针刚好到达中点的节点。
下图中蓝色指针表示快指针,橙色指针表示慢指针。
//函数中最后的判断return有问题,直接return slow即可,这样写是为了区分奇偶不同的区别
public LinkedList mid (LinkedList head) {
LinkedList fast = head;
LinkedList slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
}
if (fast == null) { //说明有偶数个节点,此时慢指针指向的是中点靠右的节点
return slow;
} else { //fast.next == null,说明有奇数个节点,此时慢指针指的恰好是中点
return slow;
}
}
2、判断链表中是否有环
如果已知一个单链表的表头,判断该链表中是否含有一个环。通常单链表都是一个节点只指向下一个节点这样的链式结构,如果只有一个指针,从头节点开始一路next,如果碰到null则表示有环,但如果没有环则会一直在环里打转,所以单指针很难解决这样的问题。
设置双指针,两个指针一快一慢,按照不同的速度从头节点开始往下遍历,如果最后两个指针相遇则表示有环,如果没有相遇,而是快指针先到了null则表示没有环。
public boolean hasCycle (LinkedList head) {
LinkedList fast = head;
LinkedList slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) { //最后两指针相遇,表示有环
return true;
}
}
return false; //若两指针不相等,则说明快指针到了null
}
3、如果链表中有环,返回环的起始位置
如果已知一个链表中含有环,要找出环的位置,返回环的起始节点。
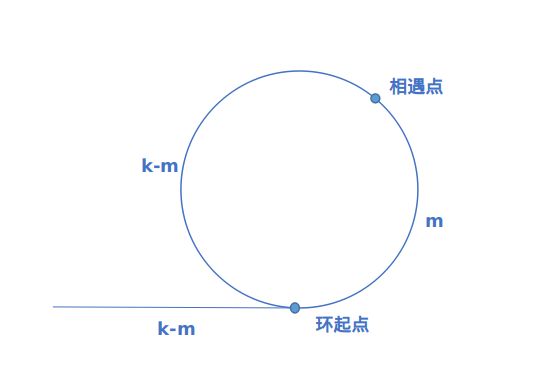
按照2中所说两个指针相遇的时候说明这个链表中有环,那么既然快指针速度是慢指针速度的二倍,那么假设两个指针第一次相遇的时候慢指针走了k步,则快指针就走了2k步,那么快指针的路程减去慢指针的路程就是环的长度,即为k。
那此时假设环的起点距离两指针的相遇点的距离为m,则从开始相遇点继续往下走,直到再次达到环起点,一共走了k-m步,而之前假设慢指针走了k步,从开始到第一次相遇,慢指针是从链表表头到第一次相遇点,走了k步,那么慢指针从表头到环的起点位置的距离也应该是k-m步(因为环起点距离相遇点是m步)。因此当两指针第一次相遇的时候,将一个指针重新置到头节点,然后两个步调一致,同样速度,每次前进一步,当再次相遇的时候,相遇位置就是环的起点。
4、求链表中环的长度
这个很简单,当两个指针第一次相遇的时候,保持快指针不动,让慢指针继续跑,两指针再次相遇的时候慢指针跑的距离就是环的长度。
5、求链表倒数第k个节点
先让某个指针走k步,然后两个指针同时走,当前面的指针走到末尾的时候,后面的指针呢恰好走到倒数第k个节点。
leetcode中的例题
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode getKthFromEnd(ListNode head, int k) {
ListNode fast = head;
ListNode slow = head;
while (k > 0) {
--k;
fast = fast.next;
}
while (fast!=null) {
fast = fast.next;
slow = slow.next;
}
return slow;
}
}
左右指针
也有叫做碰撞指针的,通常需要一个有序的数组,左右两个指针其实就是指示数组的下标,通常一个初始化在开头,一个初始化在结尾。
1、二分查找
这个是很经典的例子,在有序的数组中查找某个数(记为x),返回下标。
刚开始两个指针一前一后,判断两指针最中间的元素是否为查找的元素x,若是直接返回,如果不是且小于x,则将左指针移动到中间位置+1,即(l+r)/2 + 1,若大于x,则将右指针移动到中间位置-1。
public int BinarySearch (int[] nums, int target) {
int l = 0, r = nums.length-1;
while (l < r) {
int mid = (l + r) / 2;
if (nums[mid] == target) {
return mid;
} else if (nums[mid] > target) {
r = mid - 1;
} else {
l = mid + 1;
}
}
return -1; //表示未找到
}
2、n数之和的问题
这里以leetcode上的一个两数之和的题为例为例,如果是三数之和可以转化为一个数与两数之和的和的问题。
两数之和
给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那 两个 整数,并返回他们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素不能使用两遍。
示例:
给定 nums = [2, 7, 11, 15], target = 9
因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/two-sum
先对数组排序,设置头尾两个指针,判断相加之后与目标数的大小,如果相加之后大于目标,则移动右指针,让右指针往左滑动,使得和更小,反之则让左指针向右滑动,直到等于target。
但需要注意这道题给的并不一定是有序数组,所以并不能使用这个方法,但可以作为一个引例来启发我们,假设数组是有序的。
public int[] twoSum(int[] nums, int target) {
int[] res = new int[2];
Arrays.sort(nums);
int l = 0, r = nums.length - 1;
while (l < r) {
if (nums[l] + nums[r] == target) {
return new int[] {l,r};
} else if (nums[l] + nums[r] < target) {
l = l + 1;
} else {
r = r - 1;
}
}
return new int[] {-1,-1};
}
三数之和
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有满足条件且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例:
给定数组 nums = [-1, 0, 1, 2, -1, -4],
满足要求的三元组集合为:
[
[-1, 0, 1],
[-1, -1, 2]
]
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/3sum
正如前文所说,可以将三数之和转化为两数与一个数之和,因为要三数之和为0,先给定一个数,则另外两个数之和就得等于这个数的相反数。则可以将这两个数的和转化为上述的两数之和问题。
class Solution {
public List> threeSum(int[] nums) {
List> res = new ArrayList<>();
Arrays.sort(nums);
for (int i = 0; i < nums.length; i++) {
//剪枝,如果这个数和前一个数相等,那么由此得到的答案必和前面重复
if (i > 0 && nums[i] == nums[i-1])
continue;
int target = -nums[i]; //b+c = target
int k = nums.length-1;
for (int j = i+1; j < nums.length; j++) {
if (j > i+1 && nums[j] == nums[j-1]) //j > i+1 保证了j指针至少挪动了一次
continue;
while (j < k && nums[j] + nums[k] > target) {
k--;
}
if (j == k) { //j和k的指针重合后,没有一个k可以满足a+b+c=0 && j list = new ArrayList();
list.add(nums[i]);
list.add(nums[j]);
list.add(nums[k]);
res.add(list);
}
}
}
return res;
}
}
四数之和
给定一个包含 n 个整数的数组 nums 和一个目标值 target,判断 nums 中是否存在四个元素 a,b,c 和 d ,使得 a + b + c + d 的值与 target 相等?找出所有满足条件且不重复的四元组。
注意:
答案中不可以包含重复的四元组。
示例:
给定数组 nums = [1, 0, -1, 0, -2, 2],和 target = 0。
满足要求的四元组集合为:
[
[-1, 0, 0, 1],
[-2, -1, 1, 2],
[-2, 0, 0, 2]
]
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/4sum
继续类比前面的三数之和,不过是多了层循环而已,利用双循环先确定两个数,然后剩下的两个数就又变成了两数之和的问题,但这类问题因为有重复的元素所以要注意剪枝去掉重复的答案,还有就是数组必需有序。
class Solution {
public List> fourSum(int[] nums, int target) {
List> result = new ArrayList<>();
Arrays.sort(nums);
for (int i = 0; i <= nums.length-4; i++) {
if (i>0 && nums[i] == nums[i-1])
continue;
for (int j = i+1; j <= nums.length-3; j++) {
int tar = target - nums[i] - nums[j];
if (j>i+1 && nums[j] == nums[j-1])
continue;
for (int l = j+1; l <= nums.length-2; l++) {
if (l>j+1 && nums[l] == nums[l-1])
continue;
int r = nums.length-1;
while (r > l && nums[l] + nums[r] > tar)
r--;
if (r == l) {
break;
}
if (nums[l] + nums[r] == tar) {
List res = new ArrayList<>();
res.add(nums[i]);
res.add(nums[j]);
res.add(nums[l]);
res.add(nums[r]);
result.add(new ArrayList<>(res));
}
}
}
}
return result;
}
}
3、反转数组
将一个数组进行反转,只需要设置好前后两个指针,一个初始化指头,另一个初始化指尾,然后交换两个指针指向的内容,然后前面的指针+1,后面的指针-1,直到两指针相遇(数组大小为奇数),或者两指针相差1(数组大小为偶数)。
public void reverse (int[] nums) {
int l = 0, r = nums.length-1;
while (l < r) {
int temp = nums[l];
nums[l] = nums[r];
nums[r] = temp;
l++;
r--;
}
}
滑动窗口
其实滑动窗口应该也是左右指针中的一种,但因为它相对来说难以理解,所以单独拎出来做一讨论。
滑动窗口大概理解起来很简单,但就是自己动手写的时候会遇到很多问题,正所谓熟能生巧,笔者也才开始练这些算法题,希望记录下学习的过程。
1、无重复字符的最长子串
滑动窗口就是维护一个窗口,然后根据题目和新遇到的情况不断更新这个窗口,不断优化可能的解。举个例子,比如leetcode上的无重复字符的最长子串问题。
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3:
输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/longest-substring-without-repeating-characters
利用滑动窗口可以完美的解决这个问题,用左指针指示窗口的最左端,右指针指示窗口的最右端,初始左指针指示第0个元素,右指针指示-1,定义一个set集合存储当前解(即当前窗口中包含的字符),然后开始一直移动右指针,使其向右移动,直到碰到一个已经添加到当前解中的字符,这时记录下当前的set的大小为当前最优解,然后将左指针向右移动一个,并在当前解set中移出窗口最左边的字符。之后就是继续移动右指针,更新当前解,每次右指针碰到当前解中已存在的字符时,判断一下当前解的大小,如果比之前的最优解更优,则更新,反之不更新,继续移出窗口中最左边的字符,然后继续重复上述操作,直到右指针到达字符串末尾。
class Solution {
public int lengthOfLongestSubstring(String s) {
Set ss = new HashSet();
//定义右指针
int res = 0, r = -1;
for(int i = 0; i < s.length(); i++) {
if (i != 0) {
ss.remove(s.charAt(i-1)); //去掉上次最左边的元素
}
while (r+1 < s.length() && !ss.contains(s.charAt(r+1))) {
ss.add(s.charAt(r+1));
++r; //移动右指针
}
res = Math.max(res,r-i+1); //上次的最优和这次的最优进行对比,每次子串的开头不一样
if (r == s.length()-1) {
//r右指针已经到了最右边,所以直接break出来,因为后面不会再有向当前解中增加元素,只会慢慢弹出当前解的元素,所以不必再继续
break;
}
}
return res;
}
}
2、最小覆盖子串
给你一个字符串 S、一个字符串 T 。请你设计一种算法,可以在 O(n) 的时间复杂度内,从字符串 S 里面找出:包含 T 所有字符的最小子串。
示例:
输入:S = "ADOBECODEBANC", T = "ABC"
输出:"BANC"
提示:
如果 S 中不存这样的子串,则返回空字符串 ""。
如果 S 中存在这样的子串,我们保证它是唯一的答案。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/minimum-window-substring
1. 这道题利用滑动窗口也可以很优雅的解决,还是先初始化两个指针l = 0, r = 0指向字符串S,开始先向右移动右指针使得窗口增大,而右指针停止移动的条件是当前左指针到右指针,即窗口内已经包含了字符串T,接着开始向右移动左指针,使得窗口尽可能的小,但要确保窗口中始终是包含字符串T的,等到左指针移动到不能再移动的时候,也就是若左指针再移动一次,则窗口中将不能包含字符串T的所有字符。这时的窗口是当前解,也就是当前最优解。
2. 将其保存下来,之后向右移动一下左指针,使得窗口中不再包含T的所有字符,也就是移出去了一个T中的字符,继续向右移动右指针使其扩张,直到窗口再次包含了字符串T,然后继续移动左指针直到窗口最小,比较当前解和前面的最优解,保存下更优的。
3. 接下来就是重复操作2,直到右指针到最后一个字符后,再移动左指针,得到窗口最小的时候的解,并继续比较之前的最优解,保存更优的。
上面大概写完滑动的过程,再来说说针对这个题,实现的时候的一些细节。
- 维护一个needs数组,保存T字符串每个字符出现的次数,再维护一个window数组,保存当前窗口中各个字符的数量,后面可以根据这两个数组判断当前窗口是否包含了字符串T
- 使用一个count变量,如果当前字符属于T,而且窗口中还没有足够多的这个字符就说明这个字符目前对于窗口来说是必要的,那么把这个字符加入窗口后给count++,如果窗口中已经有了足够的这个字符,那将其加入窗口后无需给count++。而当将一个字符移出窗口时,如果移出了这个字符,窗口不再包含T的所有字符,就说明这个字符目前对于窗口来说也是必要的,那移出后给
count--,如果不是必需的则不需要减小count。这样维护下来的一个count可以指示当前窗口是否完整包含了字符串T,如果count的大小等于T的长度就说明此时的窗口完整的包含了T,这样就可以快速判断窗口是否包含T,节省了程序执行时间。
//给出的示例题解中用curr代替了window,curr记为current,表示当前的窗口
class Solution {
public String minWindow(String s, String t) {
if (s == null || s == "" || t == null || t == "" || s.length() < t.length()) {
return "";
}
int l = 0, r = 0; //定义左右指针
int size = Integer.MAX_VALUE; //窗口大小
int ans_l = 0; //最优情况下左边的指针
int count = 0;
//下面needs和curr的下标是字符的ASCII码值
int[] needs = new int[255]; //需要的
int[] curr = new int[255]; //现有的
for (int i = 0; i < t.length(); i++) { //初始化needs
needs[t.charAt(i)]++;
}
while (r < s.length()) {
char c = s.charAt(r); //当前右指针指的字符
if (needs[c] != 0) { //需要这个字符
if (curr[c] < needs[c]) { //这个字符对于目前窗口是必需的
count++;
}
curr[c]++;
}
r++;
while (count == t.length() && l < r) {
if (size > r-l) {
ans_l = l;
size = r-l;
}
char c1 = s.charAt(l);
if (needs[c1] > 0) {
if (curr[c1] == needs[c1]) { //这个字符对于目前窗口来说是必需的
count--;
}
curr[c1]--;
}
l++;
}
}
return size==Integer.MAX_VALUE?"": s.substring(ans_l,ans_l+size);
}
}