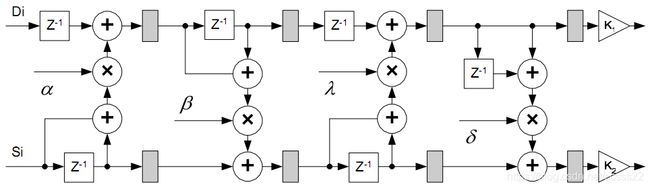
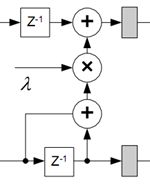
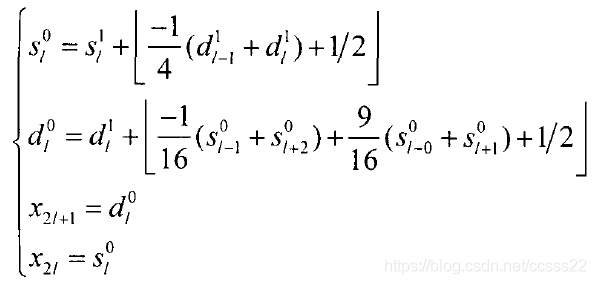97整数小波压缩的FPGA实现过程

    97整数小数变化的基本理论为：

标准在去相关模块中建议采用9/7整数小波变换，即是对原始图像先进行行变换，然后对变换后的数据再进行列变换。需要三级这样的二维小波变换，将图像分为10个子带。假设原始图像为零级小波变换后的LL0，那么后一级就是对前一级变换之后得到的LLi(i=0，1，2)再进行整数提升小波变换所得的结果。由于需要三级整数提升小波变换，每一次变换需要变换的部分的边长都为前一级的1/2，所以要求待变换的图像宽高是8的倍数。如果不满足要求，则需要对图像进行扩边处理。

CCSDS标准中采用的9/7整数小波变换就是这样一种提升小波变换，并且它只需一次提升。其算法公式可通过改变式得到：

逆变换公式如下:

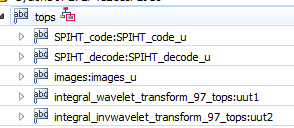
首先，FPGA的基本格式为：

分别为SPIHT编码，解码，图像ROM，小波变换，小波逆变化。

 

先介绍一下小波部分：

    在97小波变化中，四个主要参数为：

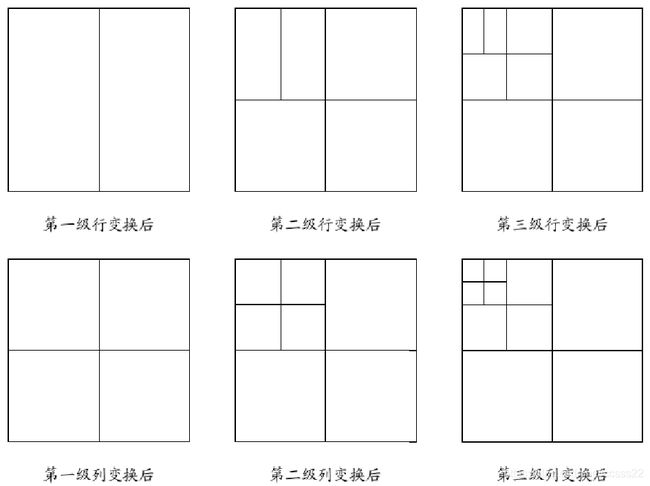
三级的二维图像提升小波变换依次以第一级行变换、第一级列变换，第二级行变换、第二级列变换、第三级行变换、第三级列变换的顺序进行，下图表示了三级变换的顺序和数据交织状况。即：

4.1 图片内源设计

    本系统所使用的测试图片为（128*128），为了方便测试数据的观察，这里，我们使用一个黑白图片作为测试信号：黑白图片如下所示：

97小波变换的FPGA实现

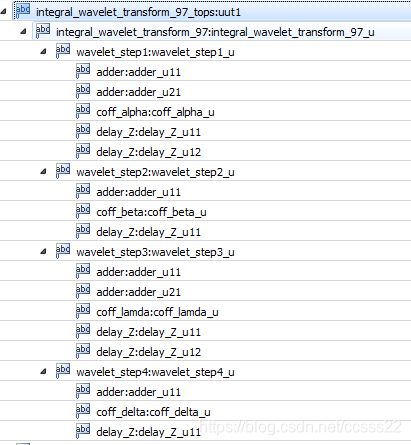
本系统，主要按照如下的结构进行设计。

   整个系统分为四个部分进行设计。

第1级，对应

第2级，对应

第3级，对应

第4级，对应

 

这么一分析，其实小波部分就比较容易理解了。

    然后小波逆变换，就是上述计算过程的逆运行。这里小波的实现方式，和matlab中的改进结构一样。采用一维的实现方式进行实现。基本上，FPGA中的程序实现方式和上面的完全一样，可以参考着看下。

然后介绍一下编码和解码两个部分：

其代码如下所示：

 

SPIHT的是实现结构基本上如下所示：

 

SPIHT算法的编码过程如下：

（1）初始化

      输出初始阈值T的指数。代码中大量的threshold就是这个阈值的设置。

 

      定义：  LSP 为空集

                  LIP = {(r,c) | (r,c)∈H }

                  LIS = {D(r,c) | (r,c)∈H 且(r,c)具有非零子孙}

      初始的LIS中各表项类型均为‘D’， LIS 和 LIP 中 (r,c) 的排列顺序与EZW算法零树结构的扫描顺序相同

 

（2）排序扫描

      1）扫描LIP队列

      对LIP队列的每个表项 (r,c) ：

            ①    输出SnOut（r,c）（函数SnOut判断(r,c)的重要性）；

            ②    如果SnOut（r,c）= 1，则向排序位流Sn输出‘1’和（r,c）的符号位（由‘1’、‘0’表示），然后将（r,c）从LIP队列中删除，添加到LSP队列的尾部。

            ③    如果SnOut（r,c）= 0，则向排序位流Sn输出‘0’。

      2）扫描LIS队列

      对LIS队列的每个表项 (r,c) ：

            ①    如果（r,c）是‘D’型表项
                  输出SnOut（D (r,c)）；

                  * 如果SnOut（D (r,c)）= 1

                          向排序位流Sn输出‘1’；

                          对每个(rO,cO) ∈O (r,c)

                              输出SnOut（rO,cO）

                              * 如果SnOut（rO,cO）= 1，则向排序位流Sn输出‘1’和（rO,cO）的符号位，将（rO,cO）添加到LSP的尾部；

                              * 如果SnOut（rO,cO）= 0，则向排序位流Sn输出‘0’，将（rO,cO）添加到LIP的尾部。

                          判断L (r,c) 是否为空集

                              如果L (r,c) 非空，则将（r,c）作为‘L’型表项添加到LIS的尾部；

                              如果L (r,c)为空集，则将‘D’型表项（r,c）从LIS中删除。

                  * 如果SnOut（D (r,c)）= 0

                          则向排序位流Sn输出‘0’。

            ②    如果（r,c）是‘L’型表项

                  输出SnOut（L (r,c)）；

                  * 如果SnOut（L (r,c)）= 1，则向排序位流Sn输出‘1’，然后将(r,c)的4个孩子（rO,cO）作为‘D’型表项依次添加到LIS的尾部，将‘L’型表项（r,c）从LIS中删除；

                  * 如果SnOut（L (r,c)）= 0，则向排序位流Sn输出‘0’。

（3）精细扫描

      将上一级扫描后的LSP列表记为LSP_Old，对于（r,c）∈ LSP_Old ，将系数Cr,c的绝对值转换为二进制表示Br,c；输出Br,c中第N个最重要的位（即对应于2^N权位处的符号‘1’或‘0’）到精细位流Rn。

    由于SPIHT编码后的LIP ，LSP ，LIS并没有作为编码器的输出，这三个列表只是用于控制编码过程，因此将SPIHT分解后的LH,HL,HH作为最低频带LL的子孙节点。

（4）更新阈值指数

     更新阈值，返回到步骤（2）进行下一级编码扫描。