作者|Christophe Pere
编译|VK
来源|Towards Datas Science
介绍
长期以来,我听说时间序列问题只能用统计方法(AR[1],AM[2],ARMA[3],ARIMA[4])。这些技术通常被数学家使用,他们试图不断改进这些技术来约束平稳和非平稳的时间序列。
几个月前,我的一个朋友(数学家、统计学教授、非平稳时间序列专家)提出让我研究如何验证和改进重建恒星光照曲线的技术。事实上,开普勒卫星[11]和其他许多卫星一样,无法连续测量附近恒星的光通量强度。开普勒卫星在2009年至2016年间致力于寻找太阳系外的行星,称为太阳系外行星或系外行星。
正如你们所理解的,我们将比我们的行星地球走得更远一点,并利用机器学习进入银河之旅。天体物理学一直是我的挚爱。
这个notebook可以在Github上找到:https://github.com/Christophe...。
RNN,LSTM,GRU,双向,CNN-x
那么我们将在哪个模型上进行这项研究?我们将使用循环神经网络(RNN[5]),LSTM[6]、GRU[7]、Stacked LSTM、Stacked GRU、双向LSTM[8]、双向GRU以及CNN-LSTM[9]。
对于那些热衷于树的人,你可以在这里找到一篇关于XGBoost和时间序列的文章,作者是jasonbrownley。github上提供了一个关于时间序列的很好的存储库:https://github.com/Jenniferz2...
对于那些不熟悉RNN家族的人,把它们看作是具有记忆效应和遗忘能力的学习方法。双向来自体系结构,它是指两个RNN,它将在一个方向(从左到右)和另一个方向(从右到左)“读取”数据,以便能够最好地表示长期依赖关系。
数据
如前文所述,这些数据对应于几颗恒星的通量测量值。实际上,在每一个时间增量(小时),卫星都会测量来自附近恒星的通量。这个通量,或者说是光强度,随时间而变化。这有几个原因,卫星的正确移动、旋转、视角等都会有所不同。因此,测量到的光子数会发生变化,恒星是一个熔化的物质球(氢和氦聚变),它有自己的运动,因此光子的发射取决于它的运动。这对应于光强度的波动。
但是,也可能有行星,系外行星,它们干扰恒星,甚至从恒星之间穿过卫星的视线(凌日方法[12])。这条通道遮住了恒星,卫星接收到的光子较少,因为它们被前面经过的行星挡住了(一个具体的例子是月球引起的日食)。
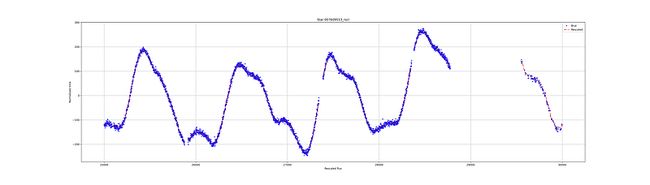
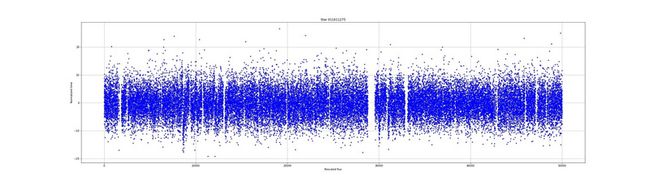
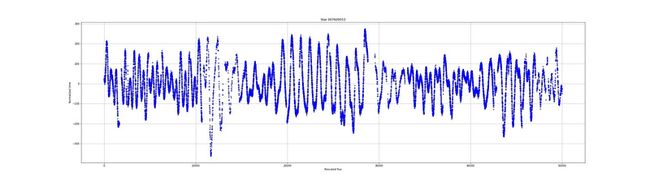
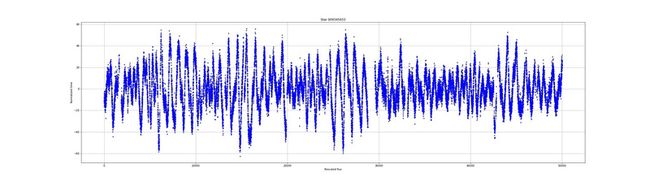
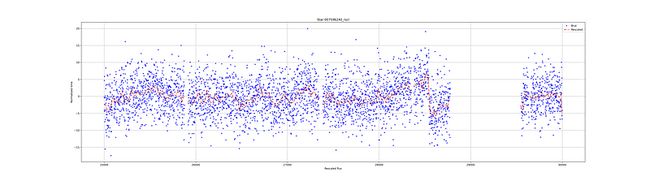
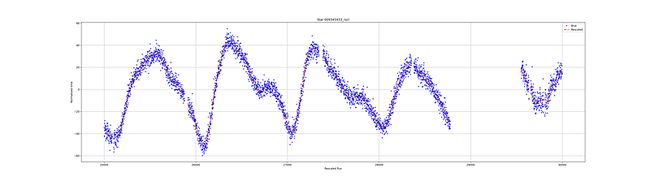
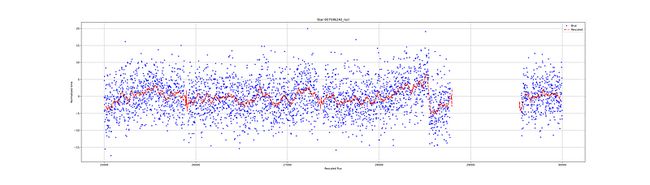
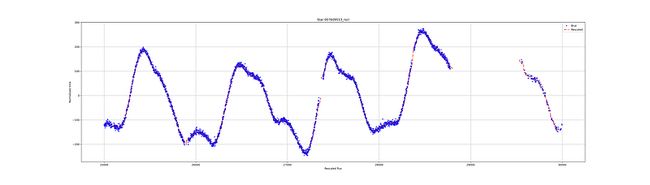
通量测量的集合被称为光曲线。光曲线是什么样子的?以下是一些示例:
不同恒星之间的通量非常不同。有的噪音很大,有的则很稳定。通量仍然呈现异常。在光照曲线中可以看到孔或缺少测量。我们的目标是看是否有可能在没有测量的情况下预测光曲线的行为。
数据缩减
为了能够使用模型中的数据,有必要进行数据简化。这里将介绍两种方法,移动平均法和窗口法。
移动平均线:
移动平均包括取X个连续点并计算它们的平均值。这种方法可以减少变异性,消除噪声。这也减少了点的数量,这是一种下采样方法。
下面的函数允许我们从点列表中计算移动平均值,方法计算点的平均值和标准差的数字。
def moving_mean(time, flux, lag=5):
'''
该函数通过设定平均值,使数据去噪,减少数据量。
@param time: (list) 时间值列表
@param flux: (list) 浮点列表->恒星通量
@param lag: (int) 平均值个数,默认值5
@return X: (list) 时间调整
@return y: (list) 通量按平均值重新标定
@return y_std: (list) 标准差列表
'''
# 让我们做一些简单的代码
# 空列表
X = []
y = []
y_std = []
j = 0 # 增量
for i in range(int(len(flux)/lag)):
X.append(np.mean(time[(i+j):(i+j+lag)]))
y.append(np.mean(flux[(i+j):(i+j+lag)]))
y_std.append(np.std(flux[(i+j):(i+j+lag)]))
j+= lag
return X, y, y_stdn 可以看到函数在输入中接受3个参数。时间和通量是时间序列的x和y。lag 是控制计算时间和通量平均值以及通量标准差时所考虑的数据个数。
现在,我们可以看看如何使用这个函数以及通过转换得到的结果。
# #导入所需的包
matplotlib inline
import scipy
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import sklearn
import tensorflow as tf
# 让我们看看进度条
from tqdm import tqdm
tqdm().pandas()现在我们需要导入数据。文件kep_lightcurves.csv包含着数据。每颗恒星有4列,原始磁通量(“…orig”),重新缩放的通量是原始磁通量减去平均磁通量(“…rscl’”)、差值(“…diff”)和残差(“…_res”)。总共52列。
# 20个数据点
x, y, y_err = moving_mean(df.index,df["001724719_rscl"], 20)df.index表示时间序列的时间
df[" 001724719_rscl "] 重新缩放的通量(" 001724719 ")
lag=20是计算平均值和std的数据点的个数
前面3条光照曲线的结果:
窗口方法
第二种方法是窗口方法,它是如何工作的?
你需要取很多点,在前一个例子中是20,然后计算平均值(与前面的方法没有区别),这个点是新时间序列的开始,它在位置20(偏移19个点)。但是,窗口不是移动到下20个点,而是移动一个点,用之前的20个点计算平均值,然后通过向后移动一步,以此类推。
这不是一种下采样方法,而是一种清理方法,因为其效果是平滑数据点。
让我们看看代码:
def mean_sliding_windows(time, flux, lag=5):
'''
该函数通过设定平均值,使数据去噪。
@param time: (list) 时间值列表
@param flux: (list) 浮点列表->恒星通量
@param lag: (int) 平均值个数,默认值5
@return X: (list) 时间调整
@return y: (list) 通量按平均值重新标定
@return y_std: (list) 标准差列表
'''
# 让我们做一些简单的代码
# 空列表
X = []
y = []
y_std = []
j = 0 # 增量
for i in range(int(len(flux)-lag)):
_flux = flux[i:(i+lag)]
_time = time[i:(i+lag)]
X.append(np.mean(_time))
y.append(np.mean(_flux))
y_std.append(np.std(_flux))
j+= 1 # 我们只移动一步
return X, y, y_std你可以很容易地这样使用它:
# 使用20个点
x, y, y_err = mean_sliding_windows(df.index,df["001724719_rscl"], 40)df.index表示时间序列的时间
df[" 001724719_rscl "] 重新缩放的通量(" 001724719 ")
lag=40是计算平均值和std的数据点的个数
现在,看看结果:
嗯,还不错。将lag设置为40允许“预测”或在小孔中扩展新的时间序列。但是,如果你仔细看,你会发现在红线的开始和结束部分有一个分歧。可以改进函数以避免这些伪影。
在接下来的研究中,我们将使用移动平均法获得的时间序列。
将x轴从值更改为日期:
如果需要日期,可以更改轴。开普勒任务开始于2009年3月7日,结束于2017年。Pandas有一个叫做pd.data_range()的函数。此函数允许你从不断递增的列表中创建日期。
df.index = pd.date_range(‘2009–03–07’, periods=len(df.index), freq=’h’)这行代码将创建一个频率为小时的新索引。打印结果如下所示。
$ df.index
DatetimeIndex(['2009-03-07 00:00:00', '2009-03-07 01:00:00',
'2009-03-07 02:00:00', '2009-03-07 03:00:00',
'2009-03-07 04:00:00', '2009-03-07 05:00:00',
'2009-03-07 06:00:00', '2009-03-07 07:00:00',
'2009-03-07 08:00:00', '2009-03-07 09:00:00',
...
'2017-04-29 17:00:00', '2017-04-29 18:00:00',
'2017-04-29 19:00:00', '2017-04-29 20:00:00',
'2017-04-29 21:00:00', '2017-04-29 22:00:00',
'2017-04-29 23:00:00', '2017-04-30 00:00:00',
'2017-04-30 01:00:00', '2017-04-30 02:00:00'],
dtype='datetime64[ns]', length=71427, freq='H')现在,对于原始时间序列,你有了一个很好的时间刻度。
生成数据集
因此,既然已经创建了数据简化函数,我们可以将它们组合到另一个函数中(如下所示),该函数将考虑初始数据集和数据集中的恒星名称(这部分可以在函数中完成)。
def reduced_data(df,stars):
'''
Function to automatically reduced a dataset
@param df: (pandas dataframe) 包含所有数据的dataframe
@param stars: (list) 包含我们想要简化数据的每个恒星的名称的列表
@return df_mean: 包含由减少平均值的数据的dataframe
@return df_slide: 包含通过滑动窗口方法减少的数据
'''
df_mean = pd.DataFrame()
df_slide = pd.DataFrame()
for i in tqdm(stars):
x , y, y_std = moving_average(df.index, df[i+"_rscl"], lag=25)
df_mean[i+"_rscl_x"] = x
df_mean[i+"_rscl_y"] = y
df_mean[i+"_rscl_y_std"] = y_std
x , y, y_std = mean_sliding_windows(df.index, df[i+"_rscl"], lag=40)
df_slide[i+"_rscl_x"]= x
df_slide[i+"_rscl_y"]= y
df_slide[i+"_rscl_y_std"]= y_std
return df_mean, df_slide要生成新的数据帧,请执行以下操作:
stars = df.columns
stars = list(set([i.split("_")[0] for i in stars]))
print(f"The number of stars available is: {len(stars)}")
> The number of stars available is: 13我们有13颗恒星,有4种数据类型,对应52列。
df_mean, df_slide = reduced_data(df,stars)很好,在这一点上,你有两个新的数据集,其中包含移动平均和窗口方法减少的数据。
方法
准备数据:
为了使用机器学习算法来预测时间序列,必须相应地准备数据。数据不能仅仅设置在(x,y)个数据点。数据必须采用序列[x1,x2,x3,…,xn]和预测值y的形式。
下面的函数演示如何设置数据集:
def create_dataset(values, look_back=1):
'''
函数准备一列(x, y)数据指向用于时间序列学习的数据
@param values: (list) 值列表
@param look_back: (int) x列表的值[x1, x2, x3,…默认值1
@return _x: x时间序列的值
@return _y: y时间序列的值
'''
# 空列表
_x, _y = [], []
for i in range(len(values)-look_back-1):
a = values[i:(i+look_back)]
_x.append(a) # 集合x
_y.append(values[i + look_back]) # 集合y
return np.array(_x), np.array(_y)开始之前有两件重要的事。
1.需要重新缩放数据
当数据在[0,1]范围内时,深度学习算法对时间序列的预测效果更好。为此,scikit learn提供了MinMaxScaler()函数。你可以配置feature_range参数,但默认值为(0,1)。并清除nan值的数据(如果不删除nan值,则损失函数将输出nan)。
# 缩放数据
num = 2 # 选择数据集中的第三颗星
values = df_model[stars[num]+"_rscl_y"].values # 提取值
scaler = MinMaxScaler(feature_range=(0, 1)) # 创建MinMaxScaler的实例
dataset = scaler.fit_transform(values[~np.isnan(values)].reshape(-1, 1)) # 数据将清除nan值,重新缩放并改变形状2.需要将数据转换为x list和y
现在,我们将使用create_values()函数为模型生成数据。但是,以前,我更喜欢通过以下方式保存原始数据:
df_model = df_mean.save()# 分成训练和测试集sets
train_size = int(len(dataset) * 0.8) # 生成80%的训练数据
train = dataset[:train_size] # 设置训练数据
test = dataset[train_size:] # 设置测试数据
#重塑为X=t和Y=t+1
look_back = 20
trainX, trainY = create_dataset(train, look_back)
testX, testY = create_dataset(test, look_back)
# 将输入重塑为[示例、时间点、特征]
trainX = np.reshape(trainX, (trainX.shape[0], trainX.shape[1], 1))
testX = np.reshape(testX, (testX.shape[0], testX.shape[1], 1))看看结果吧
trainX[0]
> array([[0.7414906],
[0.76628096],
[0.79901113],
[0.62779976],
[0.64012722],
[0.64934765],
[0.68549234],
[0.64054092],
[0.68075644],
[0.73782449],
[0.68319294],
[0.64330245],
[0.61339268],
[0.62758265],
[0.61779702],
[0.69994317],
[0.64737128],
[0.64122564],
[0.62016833],
[0.47867125]]) # x数据的第一个有20个值
trainY[0]
> array([0.46174275]) # 对应的y值度量
我们用什么指标来预测时间序列?我们可以使用平均绝对误差和均方误差。它们由函数给出:
def metrics_time_series(y_true, y_pred):
'''
从sklearn.metrics计算MAE和MSE度量
@param y_true: (list) 真实值列表
@param y_pred: (list) 预测值列表
@return mae, mse: (float), (float) mae和mse的度量值
'''
mae = round(mean_absolute_error(y_true, y_pred), 2)
mse = round(mean_squared_error(y_true, y_pred), 2)
print(f"The mean absolute error is: {mae}")
print(f"The mean squared error is: {mse}")
return mae, mse首先需要导入函数:
from sklearn.metrics import mean_absolute_error, mean_squared_errorRNNs:
你可以用几行代码轻松地用Keras实现RNN家族。在这里你可以使用这个功能来配置你的RNN。你需要首先从Keras导入不同的模型,如:
# 导入一些包
import tensorflow as tf
from keras.layers import SimpleRNN, LSTM, GRU, Bidirectional, Conv1D, MaxPooling1D, Dropout现在,我们有从Keras导入的模型。下面的函数可以生成一个简单的模型(SimpleRNN,LSTM,GRU)。或者,两个模型(相同的)可以堆叠,或者用于双向或两个双向模型的堆栈中。你还可以添加带有MaxPooling1D和dropout的CNN部分(Conv1D)。
def time_series_deep_learning(x_train, y_train, x_test, y_test, model_dl=LSTM , unit=4, look_back=20, cnn=False, bidirection=False, stacked=False):
'''
生成不同组合的RNN模型。可以是简单的、堆叠的或双向的。模型也可以与CNN部分一起使用。
x是(样本、时间步长、特征)的训练数据
@param x_train: (matrix) 训练数据,维度为 (samples, time steps, features)
@param y_train: (list) 预测
@param x_test: (matrix) 测试数据,维度为 (samples, time steps, features)
@param y_test: (list) 预测
@param model_dl: (model) RNN类型
@param unit: (int) RNN单元数量
@param look_back: (int) x列表中值的数量,配置RNN的形状
@param cnn: (bool) 添加cnn部分模型,默认为false
@param bidirection: (bool) 为RNN添加双向模型,默认为false
@param stacked: (bool) 堆叠的两层RNN模型,默认为假
@return train_predict: (list) x_train的预测值
@return train_y: (list) 真实y值
@return test_predict: (list) x_test的预测值
@return test_y: (list) 真实y值
@return (dataframe) 包含模型和度量的名称
'''
#配置提前停止的回调,以避免过拟合
es = tf.keras.callbacks.EarlyStopping(
monitor='loss', patience=5, verbose=0, mode='auto',
)
# 序列模型的实例
model = Sequential()
if cnn: # 如果cnn部分是需要的
print("CNN")
model.add(Conv1D(128, 5, activation='relu'))
model.add(MaxPooling1D(pool_size=4))
model.add(Dropout(0.2))
if not bidirection and not stacked: # 如果需要简单的模型
print("Simple Model")
name = model_dl.__name__
model.add(model_dl(unit, input_shape=(look_back, 1)))
elif not bidirection: # 测试是否需要双向模型
print("Stacked Model")
name = "Stacked_"+model_dl.__name__
model.add(model_dl(unit, input_shape=(look_back, 1), return_sequences=True))
model.add(model_dl(unit, input_shape=(look_back, 1)))
elif not stacked: # 测试是否需要堆叠模型
print("Bidirectional Model")
name = "Bi_"+model_dl.__name__
model.add(Bidirectional(model_dl(unit, input_shape=(look_back, 1))))
else: # 测试是否需要双向和堆叠模型
print("Stacked Bidirectional Model")
name = "Stacked_Bi_"+model_dl.__name__
model.add(Bidirectional(model_dl(unit, input_shape=(look_back, 1), return_sequences=True)))
model.add(Bidirectional(model_dl(unit, input_shape=(look_back, 1))))
if cnn: # 更新名称与cnn部分
name = "CNN_"+name
# 添加单层稠密层和激活函数线性来预测连续值
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam') # MSE loss可以被'mean_absolute_error'替代
model.fit(trainX, trainY, epochs=1000, batch_size=100, callbacks=[es], verbose=0)
# 做出预测
train_predict = model.predict(x_train)
test_predict = model.predict(x_test)
# 反预测
train_predict = scaler.inverse_transform(train_predict)
train_y = scaler.inverse_transform(y_train)
test_predict = scaler.inverse_transform(test_predict)
test_y = scaler.inverse_transform(y_test)
# 计算度量
print("Train")
mae_train, mse_train = metrics_time_series( train_y, train_predict)
print("Test")
mae_test, mse_test = metrics_time_series( test_y, test_predict)
return train_predict, train_y, test_predict, test_y, pd.DataFrame([name, mae_train, mse_train, mae_test, mse_test], index=["Name", "mae_train", "mse_train", "mae_test", "mse_test"]).T此函数计算训练部分和测试部分的度量,并以数据帧的形式返回结果。举五个例子。
LSTM
# 训练模型并计算度量
> x_train_predict_lstm, y_train_lstm,x_test_predict_lstm, y_test_lstm, res= time_series_deep_learning(train_x, train_y, test_x, test_y, model_dl=LSTM , unit=12, look_back=20)
# 画出预测的结果
> plotting_predictions(dataset, look_back, x_train_predict_lstm, x_test_predict_lstm)
# 将每个模型的指标保存在数据框df_results中
> df_results = df_results.append(res)GRU
# 训练模型并计算度量
> x_train_predict_lstm, y_train_lstm,x_test_predict_lstm, y_test_lstm, res= time_series_deep_learning(train_x, train_y, test_x, test_y, model_dl=GRU, unit=12, look_back=20)堆叠LSTM:
# 训练模型并计算度量
> x_train_predict_lstm, y_train_lstm,x_test_predict_lstm, y_test_lstm, res= time_series_deep_learning(train_x, train_y, test_x, test_y, model_dl=LSTM , unit=12, look_back=20, stacked=True)双向LSTM:
# 训练模型并计算度量
> x_train_predict_lstm, y_train_lstm,x_test_predict_lstm, y_test_lstm, res= time_series_deep_learning(train_x, train_y, test_x, test_y, model_dl=LSTM , unit=12, look_back=20, bidirection=True)CNN-LSTM:
# 训练模型并计算度量
> x_train_predict_lstm, y_train_lstm,x_test_predict_lstm, y_test_lstm, res= time_series_deep_learning(train_x, train_y, test_x, test_y, model_dl=LSTM , unit=12, look_back=20, cnn=True)结果
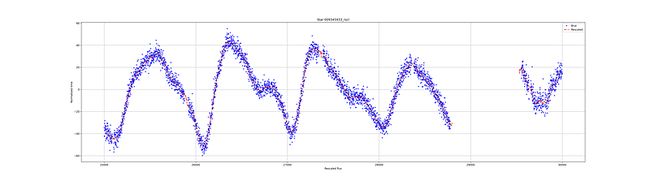
考虑到这些数据,结果相当不错。我们可以看出,深度学习RNN可以很好地再现数据的准确性。下图显示了LSTM模型的预测结果。
表1:不同RNN模型的结果,显示了MAE和MSE指标
Name | MAE Train | MSE Train | MAE Test | MSE Test
--------------------------------------------------------------------
GRU | 4.24 | 34.11 | 4.15 | 31.47
LSTM | 4.26 | 34.54 | 4.16 | 31.64
Stack_GRU | 4.19 | 33.89 | 4.17 | 32.01
SimpleRNN | 4.21 | 34.07 | 4.18 | 32.41
LSTM | 4.28 | 35.1 | 4.21 | 31.9
Bi_GRU | 4.21 | 34.34 | 4.22 | 32.54
Stack_Bi_LSTM | 4.45 | 36.83 | 4.24 | 32.22
Bi_LSTM | 4.31 | 35.37 | 4.27 | 32.4
Stack_SimpleRNN | 4.4 | 35.62 | 4.27 | 33.94
SimpleRNN | 4.44 | 35.94 | 4.31 | 34.37
Stack_LSTM | 4.51 | 36.78 | 4.4 | 34.28
Stacked_Bi_GRU | 4.56 | 37.32 | 4.45 | 35.34
CNN_LSTM | 5.01 | 45.85 | 4.55 | 36.29
CNN_GRU | 5.05 | 46.25 | 4.66 | 37.17
CNN_Stack_GRU | 5.07 | 45.92 | 4.7 | 38.64表1显示了RNN系列训练集和测试集的平均绝对误差(MAE)和均方误差(MSE)。GRU在测试集上显示了最好的结果,MAE为4.15,MSE为31.47。
讨论
结果很好,并且重现了不同恒星的光照曲线(见notebook)。然而,波动并不是完全重现的,峰值的强度也不相同,通量也有轻微的偏移。可以通过注意机制进行校正。另一种方法是调整模型、层数(堆栈)、单元数(单元)、不同RNN算法的组合、新的损失函数或激活函数等。
结论
本文展示了将所谓的人工智能方法与时间序列相结合的可能性。记忆算法(RNN、LSTM、GRU)的强大功能使得精确再现事件的偶发波动成为可能。在我们的例子中,恒星通量表现出相当强烈和显著的波动,这些方法已经能够捕捉到。
这项研究表明,时间序列不再是统计方法,如ARIMA[4]模型。
参考引用
[1] Autoregressive model, Wikipedia
[2] Moving-average model, Wikipedia
[3] Peter Whittle, 1950. Hypothesis testing in time series analysis. Thesis
[4] Alberto Luceño & Daniel Peña, 2008. Autoregressive Integrated Moving Average (ARIMA) Modeling. Wiley Online Library. https://doi.org/10.1002/97804...
[5] Rumelhart, David E. et al., 1986. Learning representations by back-propagating errors. Nature. 323 (6088): 533–536. 1986Natur.323..533R.
[6] Hochreiter, Sepp & Schmidhuber, Jürgen, 1997. Long Short-Term Memory. Neural Computation. 9 (8): 1735–1780. doi:10.1162/neco.1997.9.8.1735
[7] Cho, KyungHyun et al., 2014. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. arXiv:1412.3555
[8] M. Schuster & K.K. Paliwal, 1997. Bidirectional recurrent neural networks. IEEE Transactions on Signal Processing, Volume: 45 , Issue: 11, pp. 2673–2681. DOI: 10.1109/78.650093
[9] Tara N. Sainath et al., 2014. CONVOLUTIONAL, LONG SHORT-TERM MEMORY,FULLY CONNECTED DEEP NEURAL NETWORKS. https://static.googleusercont...
[10] Ashish Vaswani et al., 2017. Attention is all you need. https://arxiv.org/abs/1706.03762
[11] Kepler mission, Nasa
原文链接:https://towardsdatascience.co...
欢迎关注磐创AI博客站:
http://panchuang.net/
sklearn机器学习中文官方文档:
http://sklearn123.com/
欢迎关注磐创博客资源汇总站:
http://docs.panchuang.net/