Beyond Fixed Grid: Learning Geometric Image Representation with a Deformable Grid——论文阅读
| Title | Beyond Fixed Grid: Learning Geometric Image Representation with a Deformable Grid |
|---|---|
| 题目 | 超越固定网格:基于可变形网格学习几何图像表示 |
| 地址 | http://xxx.itp.ac.cn/abs/2008.09269 |
| 代码 | https://github.com/fidler-lab/deformable-grid-release |
摘要
在现代计算机视觉中,图像通常表示为具有一定步幅的固定均匀网格,并通过深度卷积神经网络进行处理。我们认为使网格变形以更好地与高频图像内容对齐是一种更有效的策略。我们介绍了可变形网格(DefGrid),这是一种可学习的神经网络模块,可预测二维三角形网格的顶点位置偏移,以使变形网格的边缘与图像边界对齐。我们在各种用例中展示了DefGrid,即通过将其作为模块插入各种处理级别。我们将DefGrid用作端到端可学习的几何降采样层,该层取代了标准池化方法,可在将图像馈入深层CNN时降低特征分辨率。与在均匀网格上使用CNN进行语义分割的任务相比,我们在相同的网格分辨率下显示出显着改善的结果。我们还在输出层使用DefGrid来完成对象蒙版注释的任务,并表明在我们预测的多边形网格上对对象边界进行推理可以比现有的基于像素和基于曲线的方法产生更准确的结果。最后,我们将DefGrid展示为一个独立的模块,用于无监督的图像划分,显示了优于现有方法的性能。
1.简介
在现代计算机视觉方法中,图像被视为具有固定步幅的固定均匀网格,并通过深度卷积神经网络进行处理。通常以较低的分辨率处理非常高分辨率的图像以提高效率,从而使图像实质上模糊并进行二次采样。当馈送到神经网络时,每个像素因此包含来自前景和背景的原始信号混合信息的模糊版本,可能导致网络对对象及其上下文的敏感度和依赖性更高。相反,在许多传统的计算机视觉流水线中,高分辨率图像被分成符合图像边界的一小组较小的超像素,从而导致在下游任务中进行更有效的推理。我们遵循这种思路,认为使网格变形以更好地与输入中的高频信息内容对齐是一种更有效的表示策略。**从概念上讲,这类似于超像素,但符合具有几何约束的规则拓扑,**因此仍很容易与深度卷积网络一起用于下游任务。
此外,诸如对象蒙版注释之类的任务自然要求输出为多边形的形式,并带有可管理数量的控制点,人类注释者可以编辑这些控制点。先前的工作要么将输出参数化为具有固定数量的控制点的闭合曲线[27],要么执行像素化标记,然后执行(不可微分)多边形化步骤[26,39,29]。在前一种方法中,预测曲线通常更好地利用形状先验来导致“表现良好”的预测,但是,输出固有地受限于其能够表示的形状的种类和复杂性。相反,逐像素方法可以表示任意属的形状,但是,通常需要较大的输入/输出分辨率才能在对象边界周围产生准确的标记。我们认为,在与图像边界很好地对齐的低分辨率多边形网格上的推理结合了两种方法的优点。
我们介绍了可变形网格(DefGrid),这是一种神经网络模块,用于表示具有二维三角形网格的图像。网格的基本元素是一个三角形单元,其顶点将三角形放置在图像平面中。 DefGrid使用统一的网格初始化,并利用神经网络预测三角形顶点的位置偏移,以使变形网格的边缘和顶点与图像边界对齐(图1)。我们提出了一些精心设计的损失函数来鼓励这种行为。由于变形操作的差异性,DefGrid可以使用下游神经网络作为即插即用模块在各种深度处理级别上进行端到端训练。我们在各种用例中展示DefGrid:这是一个可学习的几何图像降采样层,可在显着降低的网格分辨率下提供高精度的语义分割。此外,当用于对输出进行参数化时,我们证明它可以为交互式对象蒙版注释的任务带来更有效和准确的结果。我们的DefGrid也可以用作独立模块进行无监督的图像划分,并且与现有的基于超像素的方法相比,我们显示出更高的性能。

图1:DefGrid是一个神经模块,用三角形网格表示图像。 DefGrid初始化时使用统一的网格,使网格的顶点变形,以使网格的边缘与图像边界对齐,同时保持拓扑固定。
3. 可变形网格
我们的DefGrid是在图像平面上定义的二维三角形网格。网格中的基本单元是一个具有三个顶点的三角形,每个顶点的位置都将三角形放置在图像中。因此,三角形的边缘代表线段,并且预计不会在三角形之间自相交。网格的拓扑是固定的,并且不依赖于输入图像。因此,几何网格自然地将图像划分为规则块,如图1所示。
我们的方法为,让具有统一初始化的顶点位置的三角形网格变形,以更好地与图像边界对齐。网格通过神经网络变形,该神经网络可预测每个顶点的位置偏移,同时确保拓扑结构不变(不会发生自相交)。
我们的主要直觉是,当网格的边缘与图像边界对齐时,每个网格单元内的像素的RGB值变化最小,反之亦然。我们旨在以可微分的方式最小化方差依据顶点位置,以使其适合深度学习。接下来,我们将详细介绍DefGrid公式及其训练方法。在第4节中,我们将展示针对不同下游任务的应用程序。
3.1 网格参数化
3.1.1 网格拓扑
选择正确的网格拓扑是我们工作的重要方面。 由于对象(及其部分)可以在图像中以不同的比例出现,因此理想情况下,我们需要一种可以轻松再分的拓扑以适应这种多样性。 此外,可以在任何方向上找到边界,因此,网格边缘应具有足够的柔韧性以很好地与任何实际边缘对齐。 我们通过实验尝试了四种不同的拓扑结构,这些拓扑结构如图2所示。我们在最后一栏中发现该拓扑结构在表示不同边缘方向方面的灵活性优于其他方法。 请注意,我们的方法与拓扑的选择无关,我们在附录中提供了详细的比较。

图2:不同的网格拓扑。 我们选择最后一列是因为它可以灵活地表示各种不同的边缘方向。
3.1.2 网格表示
让 I I I 作为输入图像。 我们将像平面中网格的每个顶点表示为 v i = [ x i , y i ] T v_i = [x_i,y_i]^T vi=[xi,yi]T,其中 i ∈ { 1 , ⋅ ⋅ ⋅ , n } i \in \{1,···,n\} i∈{ 1,⋅⋅⋅,n}, n n n是网格中顶点的总数。 由于网格拓扑是固定的,因此图像中的网格完全由其顶点 v v v的位置指定。我们用三个顶点表示网格中的每个三角形像元,分别为 C k = [ v a k , v b k , v c k ] C_k = [v_{a_k},v_{b_k},v_{c_k}] Ck=[vak,vbk,vck],其中 k ∈ { 1 , . . . , K } k \in \{1 ,...,K\} k∈{ 1,...,K}为网格单元编制索引。 我们统一初始化2D图像平面上的顶点,并将DefGrid定义为可预测每个顶点的相对偏移的神经网络 h h h:
![]()
我们将在第4节中讨论 h h h的选择。因此,变形后的顶点为:

3.2 DefGrid的训练
现在我们讨论使用各种无监督损失函数对网格变形网络 h h h的训练。 我们希望所有损失相对于顶点位置都是可微的,以允许梯度通过分析反向传播。
3.2.1 可微分方差
随着栅格变形(其顶点移动),栅格单元将覆盖图像中的不同像素区域。 我们的第一个损失旨在最小化每个网格单元中像素特征的方差。 每个像素 p i p_i pi都有一个特征向量 f i f_i fi,在我们的情况下选择为RGB值。 如果可以使用分割掩码的形式进行监督,则可以选择附加一个代表掩码类别的one hoy向量。 图像中像素的位置用 p i = [ p i x , p i y ] T p_i = [p^x_i,p^y_i]^T pi=[pix,piy]T, i ∈ 1 , . . . , N i \in {1,...,N} i∈1,...,N表示,其中N表示图像中像素的总数。 单元 C k C_k Ck的方差定义为:
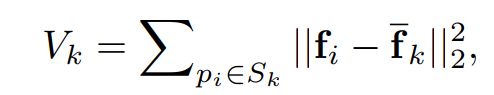
其中 S k S_k Sk表示 C k C_k Ck内的一组像素,而 f ‾ k \overline f_k fk是 C k C_k Ck的平均特征。 请注意,方差的定义相对于顶点位置不是自然地可区分的。 因此,我们将每个像素 p i p_i pi软分配给每个网格单元 C k C_k Ck来重新构造方差函数:

其中 D ( p i , v i , v j ) D(p_i, v_i, v_j) D(pi,vi,vj)是像素与线段 v i v j v_iv_j vivj之间的L1距离,而 δ δ δ是控制松弛度的超参数。 我们使用 P i → k ( V ) P_{i \to k}(V) Pi→k(V)来指示从属概率取决于网格的顶点位置,并且在我们的情况下是可微函数。 直观地,如果像素非常接近或位于像元内部,则 P i → k ( V ) P_{i \to k}(V) Pi→k(V)接近1,否则接近0。 为了检查像素是否在单元格内,我们计算该像素相对于单元格三个顶点的重心权重。 如果所有重心权重都在0和1之间,则该像素在内部,否则它将落在三角形的外部(参考判断点是否在三角形内。 现在,我们重新定义单元格的方差,如下所示:

因此,这是网格顶点位置的微分函数。 我们基于方差的损失函数旨在使所有网格单元的差异总和最小化:
3.2.2 可微分重构
受SSN [24]的启发,我们进一步使用变形的网格可微地重建图像,通过考虑从属概率 P i → k ( V ) P_{i \to k}(V) Pi→k(V)。 直观地,我们使用其平均特征 f ‾ k \overline f_k fk表示每个像元,然后根据像元变形顶点的位置将其“粘贴”到图像平面中。具体而言,我们重建图像中的每个像素通过使用 P i → k ( V ) P_{i \to k}(V) Pi→k(V):

重建损失是重建像素特征与原始像素特征之间的距离:

我们通过实验发现L1距离比L2更好.
3.2.3 正则化
为了规范化网格的形状并防止自相交,我们引入了两个正则器。 我们使用面积平衡损失函数来鼓励单元格的面积相似,从而通过最小化面积的方差来避免自相交:

其中 a ‾ \overline a a是平均面积, a k a_k ak是单元格 C k C_k Ck的面积。 在3D网格预测[38,8]上,我们还利用Laplacian正则化。 特别是,这种损失会促使相邻顶点相对于中心顶点沿相似方向移动:

其中 Δ i = [ Δ x i , Δ y i ] T \Delta_i = [\Delta_{x_i}, \Delta_{y_i}]^T Δi=[Δxi,Δyi]T是顶点 v i v_i vi的预测偏移,而 N ( i ) N(i) N(i)是顶点 v i v_i vi的相邻顶点的集合。
训练我们的网络 h h h的最终损失是上述所有条件的加权和:
![]()
4. 应用
我们的DefGrid支持当今在固定图像网格上完成的许多计算机视觉任务。我们在本节中讨论三种可能的用例。 DefGrid可以作为即插即用模块插入多个处理级别。通过将其插入输入级别,我们将DefGrid用作可学习的几何下采样层,以替代标准的池化方法。我们将在4.1节中通过应用到语义分割来展示其有效性。我们在第4.2节中进一步展示了对象蒙版注释的应用,其中我们提出了一个模型,该模型基于深度DefGrid输出的边界对齐网格来生成对象多边形。最后,在第4.3节中,我们将DefGrid展示为用于无监督图像划分的独立模块。
4.1 可学习的几何下采样
复杂场景的语义分割通常需要高分辨率图像作为输入,因此会产生计算量大的高分辨率特征图。现有的深层CNN通常将降采样后的图像作为输入,并使用特征池和Bottleneck结构来减轻内存使用量[18,19,42]。我们认为,使用DefGrid对特征进行下采样可以保留更好的几何信息。给定任意深度的CNN架构,我们建议使用浅层CNN编码器插入DefGrid来预测变形的网格。预测的保留边界的网格可用于感知几何的特征池化。具体来说,为了表示每个像元,我们可以通过平均或选择每个三角形像元中的最大特征值来应用均值或最大池化。由于规则的网格拓扑,这些特征可以直接传递到标准CNN。请注意,网格池化操作会将原始特征图从图像坐标扭曲为网格坐标。因此,通过检查像素位于哪个网格单元格中,将最终输出(预测的语义分割)粘贴回图像平面。完整的pipeline是端到端可微分的。我们可以以多任务的方式联合训练模型,其中包含语义分割分支的交叉熵损失和上述网格变形损失。 DefGrid模块是轻量级的,因此具有最小的计算开销。该架构如图3所示。
4.2 对象蒙版注释
给定用户提供的边界框,对象蒙版注释是描绘前景对象轮廓的问题[7,3,27,29,39]。已经提出了两种主要方法来解决该任务。第一种方法利用深度神经网络来预测像素级蒙版[29,39,26]。第二种方法试图用多边形/样条线[20,14,7,3,27]勾勒出边界。我们的DefGrid支持这两种方法,并通过基于多边形网格的推理对其进行了改进(图4)。
4.2.1 基于边界的分割
我们将基于边界的分割公式化为最小能量路径搜索问题。我们沿着网格边缘搜索距离变换能量最小的闭合路径:
其中Q表示网格上所有可能路径的集合,M表示路径Q的长度。我们首先使用经过L2损失训练的深层网络预测对象的距离变换能量图。然后,我们通过双线性采样计算每个网格顶点中的能量。我们通过平均沿两个顶点定义的直线上的点的能量值来获得每个网格边缘的能量。请注意,直接在网格上搜索可能会导致许多局部最小值。我们使用Curve-GCN [27]来预测40个种子点,并将这些点中的每一个捕捉到在其前k个最接近顶点中能量最小的网格顶点。然后,对于每个相邻的种子点对,我们使用Dijkstra算法找到它们之间的最小能量路径。我们在附录中提供了算法的详细信息。我们的方法在两个方面对Curve-GCN进行了改进:1)由于它在边界对齐的网格上明确地说明了原因,因此可以更好地与图像边界对齐; 2)由于我们在Curve-GCN输出的相邻点之间寻找最小的能量路径,因此这种方法可以处理边界更复杂的对象,而这些边界只能用40个点来表示。
4.2.2 逐像素分割
我们不会生成逐像素蒙版,而是预测每个网格单元的类标签。具体来说,我们首先使用深度神经网络从图像中获取特征图。然后,对于每个网格单元,我们平均合并该单元内所有像素的特征,并使用MLP网络预测每个单元的类别标签。用交叉熵损失训练模型。由于网格边界与对象边界很好地对齐,因此将特征合并到网格内对于学习而言更加有效。
4.3 无监督图像划分
我们已经可以将变形的三角形单元视为“超像素”,并通过无监督的损失函数进行训练。我们可以进一步利用它们之间的亲和力对单元进行聚类。特别是,我们将变形的网格视为无向加权图,其中每个网格单元是一个节点,如果两个边共享网格中的一条边,则一条边连接两个边,每个边的权重是两个像元之间的亲和力,可以使用像元内部像素的RGB值进行计算。
可以使用不同的聚类技术,并且探索所有内容超出了本文的范围。为了展示DefGrid作为无监督图像分割方法的有效性,我们在这里利用简单的贪婪凝聚聚类。我们将合并后的平均亲和度表示一个新节点。当我们达到所需的超像素数量或亲和力低于阈值时,聚类停止。请注意,根据设计,我们的超像素是多边形。请注意,我们的框架自然支持监督损失函数,但是在本文中我们不对其进行探讨。
5. 实验
我们在下游任务中来评估DefGrid。我们首先展示了在可学习的下采样中进行语义分割的应用。然后,我们使用基于边界的方法和按像素的方法评估对象注释任务。最后,我们展示了DefGrid在无监督图像分区中的有效性。
5.1 可学习的几何下采样
为了验证DefGrid作为有效的下采样方法的有效性,我们将(固定)图像网格特征池化方法作为基准,即Cityscapes [9]语义分割基准上的最大/平均池化和步长卷积作为基准。基线方法在浅层特征图上执行最大/平均池化或步幅卷积,而我们的网格池化方法在变形的三角形像元上应用最大/平均池化。当特征图的高度和宽度被下采样到原始图像尺寸的1/4、1/8、1/16和1/32时,我们将网格池化与基线进行比较。我们使用改良的ResNet50 [18],它比SOTA模型[35]更轻便。
评估指标:与[39,26,27]相同,我们使用mIoU和边界F分数(在完整图像上阈值为4和16像素)评估性能。所有指标均在所有类别中平均。
结果:表1中报告了性能(mIoU和边界F分数)。我们的DefGrid合并方法始终优于基线,尤其是在边界分数上。我们受益于DefGrid坐标的edge-aligned属性。从1/4的下采样到1/8,由于缺少小目标实例,基准性能显著下降,而我们的DefGrid池化方法可以更优雅地应对此问题。当下采样率较小时,我们也优于基线,这表明有限空间容量的有效利用。我们在图5中可视化了预测网格的定性结果。我们的DefGrid更好地与边界对齐,因此,下游网络“看到”的内容比固定的统一网格更具信息性。