-
最小二乘法
在线性回归中,听的最多的应该算是最小二乘法了。最小二乘法在具体实现过程中保留核心思想的同时,会在算法上进行不同程度的改进,因此,最小二乘法有很多演变体,例如:递推最小二乘法,加权最小二乘法。这些都会根据实际情况而变化。本文,主要讲一下我对最小二乘法的理解。
所谓“最小二乘法”,least squares method,从字面上看,least就是一个最优化问题的体现,因此,最小二乘法是一个最优化问题(optimization problem)。
概念
-
什么是回归
我的理解:当自变量和因变量存在某种函数关系可以用来近似描述时,我们把这种行为叫做回归。而这个函数叫做回归函数。
-
回归的意义
回归可以帮助我们对因变量进行预测,根据以往的数据和回归函数,我们能大致预测接下来的因变量的走势。这个在股市上用的很多,在一些时间序列问题上也应用广泛。
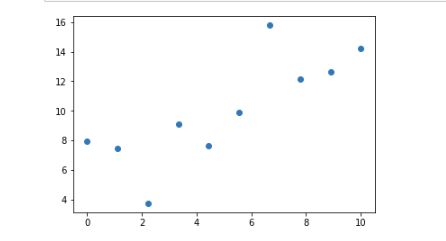
我们假设我们有一组数,
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import random
x=np.linspace(0,10,10)
random.seed()
y=np.linspace(5,15,10)+[random.uniform(-5,5) for _ in range(10)]
print(y)
plt.scatter(x,y)
plt.show()
生成了一组随机数,然后我们想用一种函数来描述横轴x和纵轴y的关系,我们先假设是线性关系,hypothesis function就为H(x)=\theta_0+\theta_1*x
如果我们得到了\theta_0, \theta_1,那么我们的回归函数就得以确定。通过x就可以计算出对应的y。
如何得到H(x)
要让我们的假设函数对真实数据描述性更强,也就是假设函数更接近真实数据的分布。那么他们两者之间的误差就应该达到最小。
于是,我们得到cost function,
J(\theta_0, \theta_1)=\frac{1}{2m}\sum_{i=1}^m(H(x^{(i)})-y^{(i)})^2
对每个离散值和计算值进行误差平方再求和计算总误差。
这时候,我们目标就是计算:
minimize J(\theta_0, \theta_1)
以上就是最小二乘法的概念。
-
梯度下降法
最小二乘法是一种优化问题的想法,梯度下降法是实现这种优化想法具体的一种求解方法。
在最小二乘法问题中求解minimize J(\theta_0, \theta_1)过程中,如果是线性问题,我们可以尝试用矩阵也就是normal equation。这里只需要确保(x^Tx)^{-1}是存在的。当然这也是矩阵计算的一个局限性。
正常比较万能的方法,就是梯度下降法(不要说他慢)。
梯度下降法的本质就是迭代。通过迭代更新\theta值,逐渐找到J(\theta_0,\theta_1)的最小值。
从上图可以发现,纵轴的J值随着横轴迭代次数的增加,逐渐变小。
算法思路
我们已知cost function J(\theta_0, \theta_1)=\frac{1}{2m}\sum_{i=1}^m(H(x^{(i)})-y^{(i)})^2
我们的目标函数是minimize J(\theta_0, \theta_1)
因此,让J(\theta_0, \theta_1)分别对 \theta_0, \theta_1求偏导。
得到,
\frac{\partial J(\theta_0, \theta_1)}{\partial \theta_0} = \frac{1}{m}\sum_{i=1}^m(x^{(i)})-y^{(i)})
\frac{\partial J(\theta_0, \theta_1)}{\partial \theta_1} = \frac{1}{m}\sum_{i=1}^m(x^{(i)})-y^{(i)})x_i
对\theta进行更新:
\theta_0: \theta_0-\alpha \frac{\partial J(\theta_0)}{\partial \theta_0}
\theta_1: \theta_1-\alpha \frac{\partial J(\theta_1)}{\partial \theta_1}
thetaSet=np.array(thetaSet)
J=np.zeros((50,50))
theta0Max,theta0Min=max(thetaSet[:,0]),min(thetaSet[:,0])
theta1Max,theta1Min=max(thetaSet[:,1]),min(thetaSet[:,1])
theta0=np.linspace(0,1.8,50)
theta1=np.linspace(0,1.8,50)
T0,T1=np.meshgrid(theta0,theta1)
for i in range(50):
for j in range(50):
J[i,j]=sum((theta0[i]+theta1[j]*x-y)**2)/len(x)
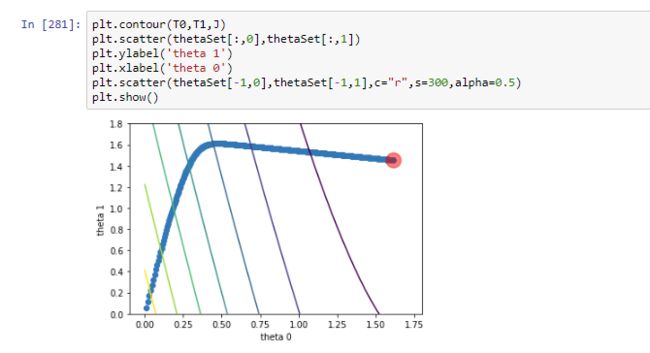
plt.contour(T0,T1,J)
plt.scatter(thetaSet[:,0],thetaSet[:,1])
plt.ylabel('theta 1')
plt.xlabel('theta 0')
plt.scatter(thetaSet[-1,0],thetaSet[-1,1],c="r",s=300,alpha=0.5)
plt.show()
在这里五彩线是梯度线,我们可以看出,我们初始\theta为[0,0],然后\theta逐渐向最小cost逼近,最后到达[1.6,1.6]的位置。
在梯度下降法里,我们还会有增量梯度下降法等等,但都是为了更快实现逼近而设计的,这个根据具体需求具体分析。