线性表——链表
链表
文章目录
- 链表
-
- 概念
- 单链表
-
- 单链表的构造
-
- `结点初始化`
- 头结点
- 头插法建表
- 尾插法建表
- 单链表基本操作
-
- 插入
- 查找
-
- 按值查找
- 按序号查找
- 删除
- 完整代码
- 单链表约瑟夫环
- 其他链表
-
- 循环链表
- 双向链表
-
- 注意(待解决)
- 顺序表与链表比较
概念
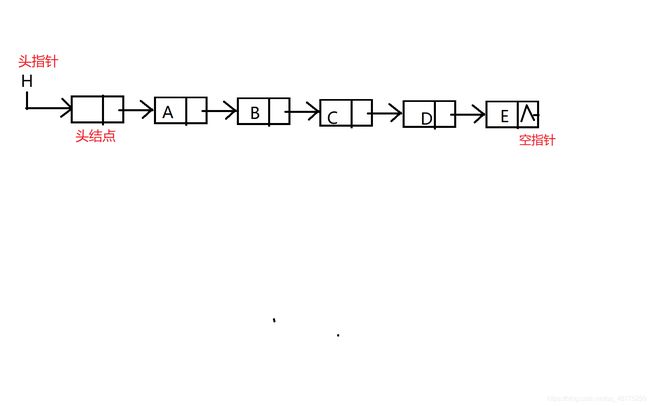
采用链式存储结构的的线性表称为链表,链表中每个结点包含存放数据元素值的数据域和存放指向逻辑上相邻结点的指针域(地址域),只有一个指针域指向后一个结点的叫做单链表,有两个指针域指向前后两个结点的叫做双链表。在使用链表时只关心逻辑顺序而不用在意存储位置,这是因为链表存储位置是零散的、碎片化的
单链表
单链表的构造
结点初始化
public class Node{
Object data; //数据域,保存数据元素
Node next; //地址域,保存下一个元素的地址,指向后继
public Node(){
//构造一个无参的构造函数,可实现初始化一个空的结点
this(null,null);
}
public Node(Object data){
//构造一个带一个data参数的构造方法,可实现构造一个数据域为指定参数值而指针域为空的结点
this(data,null);
}
public Node(Object data, Node next){
//构造一个带俩参数的构造方法,可实现构造一个数据域和指针域都为指定参数值的结点
this.data = data;
this.next = next;
}
}
头结点
头结点用head表示
由单链表示意图我们可知链表中需要一个头结点,此头结点可由结点初始化的无参构造函数来完成
public class LinkList{
public Node head;
public LinkList(){
this.head = new Node(); //调用`结点初始化`中的无参构造函数完成对头结点的建立
}
public LinkList(int n,boolean Order,Object[] temp)throws Exception{
//构造一个长度为n的单链表
this(); //置一个只有头结点的空表
//后续步骤为调用方法建表
}
}
在有一个头结点的情况下,我们可以用头插法或尾插法进行建表
头插法建表
通过调用前面方法进行
//头插法建表基本理念为永远在头结点后,首结点前插入新的结点
public void createHead(int n)throws Exception{
Scanner input = new Scanner(System.in);
for(int j = 0; j < n; j++)
insert(0,input.next());
input.close();
}
自行书写
// 头插法
public void create2(Object[] temp) throws Exception{
//将Demo中的数组进行传递
// Node head = this.head; //头结点
if(temp == null)
throw new Exception("空对象异常");
if(temp.length == 0)
System.out.println("传递数组为空");
for (int i = 0; i < temp.length; i++) {
//利用for循环进行逐个插入
Node node = new Node(temp[i],null); //建立新结点
node.next = this.head.next; //将原本首结点的地址赋予给新结点
this.head.next = node; //将新结点地址赋予首结点
}
}
尾插法建表
调用前面方法完成
public void createRear(int n) throws Exception throws Exception{
Scanner input = new Scanner(System.in);
System.out.println("请输入元素");
for(int j = 0; j < n; j++)
insert(length(), input.next());
input.close();
}
自行书写
//尾插法基本理念为在最后一个结点后面加新的结点
public void createRear(Object[] temp)throws Exception{
Node rear = this.head; //尾指针rear
if(temp == null)
throw new Exception("空对象异常");
if(temp.length == 0)
System.out.println("链表为空");
for(int i = 0; i < temp.length; i++){
rear.next = new Node(temp[i], null);
rear = rear.next; //尾指针自赋值,指向新的尾结点
}
}
上述头插法方法中涉及链表的插入方法
单链表基本操作
插入
单链表的插入操作我们实际上只需要改变两个地方,需要插入结点位置的前一个结点的地址域,需要插入结点的地址域
插入代码块
public void insert(int i, Object x) throws Exception{
if(x == null)
throw new Exception("不能插入空对象");
Node p = this.head; //p指向头结点
for(int j = 0; p.next != null && j < i; j++) // 寻找插入位置
p = p.next;
p.next = new Node(x, p.next);
}
查找
单链表的查找我们一般采用遍历的查询方法,因为,在链表中没有索引,只有通过从表头开始一个一个往下寻找,当前结点也只知道它的后继的地址
按值查找
public int search(Object key) throws Exception{
if(key == null)
throw new Exception("需要寻找元素为空");
int i = -1;
for(Node p = this.head.next; p != null; p = p.next){
//p这里指向头结点,不是首结点;p自赋值
i++;
if(p.data.equals(key)) //p指向结点的数据域与需要寻找元素进行对比
return i; //返回位置
}
throw new Exception("该链表无此元素");
}
按序号查找
public Object get(int i) throws Exception{
if(i < 0) //防御代码
throw new Exception("序号输入错误!");
Node p = head.next; //初始化,p指向首结点地址域,j为计数器
int j = 0;
while(p != null && j < i){
//当p指向结点地址域(当前p指向头结点)不为空且计数器小于需要查找需要时进行循环
p = p.next; //p自赋值后移
++j; //计数器++
}
if(j > i || p == null){
//当计数器值大于序号或p指向结点为空(即尾结点)时说明需要查找元素不存在
throw new Exception("第" + i + "个元素不存在");
}
return p.data; //返回p的地址域
}
删除
当我们需要删除单链表中某个结点时,通常我们需要先找到它,然后再进行删除操作,链表删除相对于顺序表更加简单快捷,只需要改变地址域指向即可,同顺序表中,我们也应对删除的元素进行保存
// 删除带头结点的单链表中的第i个结点
public Object remove(int i) throws Exception{
if(i >= 0 && i < length()){
Node p = this.head; //p目前为头指针
//定位到待删除结点(i)的前驱结点(i - 1)
for(int j = 0; p.next != null && j < i; j++){
p = p.next;
}
if(p.next != null){
Object old = p.next.data;//获取原对象
p.next = p.next.next;//删除p的后继结点
return old;
}
}
//当i < 0或大于表长时
return null;
}
完整代码
public class LinkList02 {
public Node head;
public LinkList02(){
this.head = new Node(); //调用结点初始化中的无参构造函数完成对头结点的建立
}
public LinkList02(int n,boolean Order,Object[] temp)throws Exception{
//构造一个长度为n的单链表
this(); //置一个只有头结点的空表
if(Order)
create1(temp);
else
create2(temp);
}
// 尾插法
public void create1(Object[] temp)throws Exception{
Node rear = this.head; //尾指针rear
if(temp == null)
throw new Exception("空对象异常");
if(temp.length == 0)
System.out.println("链表为空");
for(int i = 0; i < temp.length; i++){
rear.next = new Node(temp[i], null);
rear = rear.next; //尾指针自赋值,指向新的尾结点
}
}
// 头插法
public void create2(Object[] temp) throws Exception{
//将Demo中的数组进行传递
Node head = this.head; //头指针
if(temp == null)
throw new Exception("空对象异常");
if(temp.length == 0)
System.out.println("传递数组为空");
for (int i = 0; i < temp.length; i++) {
//利用for循环进行逐个插入
Node node = new Node(temp[i],null); //建立新结点
node = head.next; //将原本首结点的地址赋予给新结点
head.next = node; //将新结点地址赋予首结点
}
}
//将一个已经存在的带头结点单链表制成空表
public void clear(){
head.data = null;
head.next = null;
}
// 判断带头结点的单链表是否为空
public boolean isEmpty(){
return head.next == null;
}
// 求带头结点的单链表的长度
public int length(){
Node p = head.next; //初始化,p指向首结点,length为计数器
int length = 0;
while(p != null){
//从首结点开始向后查找,直到p为空
p = p.next; //指向后继结点
++length; //长度增1
}
return length;
}
//按值查找
public int search(Object key) throws Exception{
if(key == null)
throw new Exception("需要寻找元素为空");
int i = -1;
for(Node p = this.head.next; p != null; p = p.next){
//p这里指向头结点,不是首结点;p自赋值
i++;
if(p.data.equals(key)) //p指向结点的数据域与需要寻找元素进行对比
return i; //返回位置
}
throw new Exception("该链表无此元素");
}
// 读取带头结点的单链表中的第i个结点
public Object get(int i) throws Exception{
if(i < 0) //防御代码
throw new Exception("序号输入错误!");
Node p = head.next; //初始化,p指向首结点,j为计数器
int j = 0;
while(p != null && j < i){
p = p.next;
++j;
}
if(j > i || p == null){
throw new Exception("第" + i + "个元素不存在");
}
return p.data;
}
// 在带头结点的单链表中的第i个结点之前插入一个值为x的新节点
public void insert(int i, Object x) throws Exception{
if(x == null)
throw new Exception("不能插入空对象");
Node p = this.head; //p指向头结点
for(int j = 0; p.next != null && j < i; j++) // 寻找插入位置
p = p.next;
p.next = new Node(x, p.next);
}
// 删除带头结点的单链表中的第i个结点
public Object remove(int i) throws Exception{
if(i >= 0 && i < length()){
Node p = this.head; //p目前为头指针
//定位到待删除结点(i)的前驱结点(i - 1)
for(int j = 0; p.next != null && j < i; j++){
p = p.next;
}
if(p.next != null){
Object old = p.next.data;//获取原对象
p.next = p.next.next;//删除p的后继结点
return old;
}
}
//当i < 0或大于表长时
return null;
}
// 在带头结点的单链表中查找值为x的结点
public int indexOf(Object x){
Node p = head.next; //初始化,p指向首结点,j为计数器
int j = 0;
// 下面从单链表中的首结点开始查找,直到p.data为x或到达单链表的表尾
while(p != null && !p.data.equals(x)){
p = p.next; //指向下一个结点
++j; //计数器+1
}
if(p != null)
return j; //返回值为x的结点在单链表中的位置
else
return -1; //值为x的结点不在单链表中,则返回-1
}
// 输出单链表中的所有结点
public void display(){
Node node = head.next; //取出带头结点的单链表中的首结点
while(node != null)
{
System.out.print(node.data + " "); //输出结点的值
node = node.next; //取下一个结点
}
System.out.println(); //换行
}
//循环链表的实现
public void loop(Object[] temp){
Node rear = this.head;
for(int i = 0; i < temp.length; i++){
rear.next = new Node(temp[i], null);
rear = rear.next; //尾指针自赋值,指向新的尾结点
}
rear.next = this.head.next;
}
}
public class Node {
Object data; //数据域
Node next; //地址域
public Node(){
//构造一个无参的构造函数,可实现初始化一个空的结点
this(null,null);
}
public Node(Object data){
//构造一个带一个data参数的构造方法,可实现构造一个数据域为指定参数值而指针域为空的结点
this(data,null);
}
public Node(Object data,Node next){
//构造一个带俩参数的构造方法,可实现构造一个数据域和指针域都为指定参数值的结点
this.data = data;
this.next = next;
}
}
单链表约瑟夫环
类同于顺序表约瑟夫环问题,代码如下
public class Josephus02 {
public static void count(int n){
//数到3出局,中间间隔两个人
int k = 3;
//头结点不存储数据
Node head = new Node();
Node cur = head;
//循环构造这个链表
for(int i=1; i<=n; i++){
Node node = new Node(i);
cur.next = node;
cur = node;
}
//链表有数据的部分首尾相连形成一个环。
cur.next = head.next;
//统计开始的时候,刨去头结点,然后从第一个有数据的结点开始报数
Node p = head.next;
//循环退出的条件是最后只剩一个结点,也就是这个结点的下一个结点是它本身
while(p.next!=p){
//正常报数的遍历逻辑
for(int i=1;i<k-1;i++){
p = p.next;
}
//当数到3的时候,出局
System.out.print(p.next.data+",");
p.next = p.next.next;
p = p.next;
}
//最后剩下的一个结点
System.out.println();
System.out.println("最后赢家:"+p.data);
}
public static void main(String[] args) {
count(8);
}
}
class Node{
int data;
Node next;
public Node(){
}
public Node(int data){
this.data = data;}
}
其他链表
循环链表
即环形链表,结构与单链表相似。即单链表的最后一个结点的后继指针指向第一个结点,从而构成一个环形链表,继而此链表每一个结点都有后继,地址域均不为空
Node p = tailb.next; //p指向第二个表的头结点
tailb.next = taila.next; //第二个表的表尾与第一个表的表头相连接
taila.next = p.next; //第一个表的表尾与第二个表的首结点相连
循环链表一般会采用尾指针,因为在实际中,采用尾指针找循环链表最后一个结点和第一个结点时算法复杂度都为O(1)
循环链表的实现
//循环链表的实现
public void loop(Object[] temp){
Node rear = this.head;
for(int i = 0; i < temp.length; i++){
rear.next = new Node(temp[i], null);
rear = rear.next; //尾指针自赋值,指向新的尾结点
}
rear.next = this.head.next; //使尾结点指针域指向头结点
}
双向链表
双向链表不同于单链表,它拥有两个指针域,分别指向其前驱和后继
双链表与单链表只在插入和删除上有较大差异,其他基本与单链表无异
下面给出完整代码
方法类
import java.util.Scanner;
public class DuLinkList {
DuLNode head;
public DuLinkList(){
head = new DuLNode();
head.prior = head;
head.next = head;
}
//双向链表构建
public DuLinkList(int n) throws Exception{
this();
Scanner input = new Scanner(System.in);
for (int j = 0; j < n; j++)
insert(0,input.next());
input.close();
}
// 插入
public void insert (int i, Object x) throws Exception{
DuLNode p = head.next; //指针p指向头结点
int j = 0; //计数器
while( !p.equals(head) && j < i){
//当p不等于头指针本身(指向本身则说明为空表且计数器效于插入位置时
p = p.next; //自赋值
++j; //计数器++
}
if(j != i && p.equals(head)) //防御代码
throw new Exception("插入位置不合法");
DuLNode s = new DuLNode(x); //新结点
p.prior.next = s; //将s的地址赋给p前结点的后指针域
s.prior = p.prior; //将原p前面一个结点的地址赋给s的前指针域
s.next = p; //将p的地址赋给s的后指针域
p.prior = s; //将s的地址赋给p的前指针域
}
//删除
public void remove(int i ) throws Exception{
DuLNode p = head.next; //p指向头结点
int j = 0; //计数器
while( !p.equals(head) && j < i){
p = p.next;
++j;
}
if(j != i)
throw new Exception("删除位置不合法");
p.prior.next = p.next; //p指向的前一个结点的后指针域指向p的后一个结点
p.next.prior = p.prior; //p指向的后一个结点的前指针域指向p的前一个结点
}
//将一个已经存在的带头结点双链表制成空表
public void clear(){
head.data = null;
head.next = null;
head.prior = null;
}
//判断带头结点的双链表是否为空
public boolean isEmpty(){
return head.next == null;
}
//读取带头结点的双链表中的第i个结点
public Object get(int i)throws Exception{
DuLNode p = head.next; //初始化头结点指针域
int j;
for( j = 0; p != null && j < i; ++j)
p = p.next;
if(j > i || p == null)
throw new Exception("第" + i + "个元素不存在");
return p.data;
}
//获取带头结点的双链表的长度
public int length(){
DuLNode p = head.next; //初始化,p指向头结点
int length = 0; //表长计数器
if(p == null){
return length;
}
while(!p.equals(head)){
//从首结点开始向后查找,直到p为空
p = p.next; //指向后继结点
++length; //长度增1
}
// ++length; //自赋值
return length; //返回长度
}
//在带头结点的双链表中查找值为x的结点
public int indexOf(Object x){
DuLNode p = head.next; //初始化,p指向首结点,j为计数器
int j = 0;
// 下面从单链表中的首结点开始查找,直到p.data为x或到达单链表的表尾
while(p != null && !p.data.equals(x)){
p = p.next; //指向下一个结点
++j; //计数器+1
}
if(p != null)
return j; //返回值为x的结点在单链表中的位置
else
return -1; //值为x的结点不在单链表中,则返回-1
}
//输出所有结点
public void display(){
DuLNode node = head.next;
while( !node.equals(head)){
System.out.print(node.data + " ");
node = node.next;
}
System.out.println();
}
}
结点构造
public class DuLNode {
Object data; //数据域
DuLNode prior; //前驱结点
DuLNode next; //后继节点
public DuLNode(){
this(null,null,null);
}
public DuLNode(Object data){
this(data, null, null);
}
public DuLNode(Object data, DuLNode prior){
this(data,prior,null);
}
//构造数据域值为data的结点
public DuLNode(Object data, DuLNode prior, DuLNode next) {
this.data = data;
this.prior = prior;
this.next = next;
}
}
注意(待解决)
在双链表中使用遍历似乎只能用!p.equals(head),若使用p != null判断条件进行遍历时会出现死循环,而单链表中则不会出现这个错误,但是若单链表使用!p.equals(head)会出现空指针异常…
顺序表与链表比较
顺序表随机存取效率高,但是插入和删除效率较慢在时间复杂度上查找O(1);插入和删除O(n),需要预先分配空间,容易出现溢出问题
链表插入和删除效率高,但查找速度慢,原理上没有空间限额,可以无上限存储,实际上与空间大小有关,查找O(n);删除O(1)。
所以我们 在采用时应当根据实际情况而定。