2018激光样式
题目描述
x星球的盛大节日为增加气氛,用30台机光器一字排开,向太空中打出光柱。
安装调试的时候才发现,不知什么原因,相邻的两台激光器不能同时打开!
国王很想知道,在目前这种bug存在的情况下,一共能打出多少种激光效果?
显然,如果只有3台机器,一共可以成5种样式,即:
全都关上(sorry, 此时无声胜有声,这也算一种)
开一台,共3种
开两台,只1种
30台就不好算了,国王只好请你帮忙了。
输出
输出一个整数表示答案
动态规划
#include
using namespace std;
int main() {
//freopen("in.txt", "r", stdin);
ios_base::sync_with_stdio(false), cin.tie(0), cout.tie(0);
int n = 30, a[31] = { 0,2,3 };
//类似斐波那契数列的递推
for (int i = 3; i <= n; ++i)a[i] = a[i - 1] + a[i - 2];
cout << a[n];
}
//2178309
DFS搜索
#include
using namespace std;
int cnt = 0,n = 30;
bool vis[40];
/*
dfs(i) 第i个激光机器 有两种选择:vis[i-1] == 0 时 可选,无论vis[i-1]为何值都不选
vis[i] 回溯标记是否用过
*/
void dfs(int x) {
if (x == n + 1) { cnt++; return; }
dfs(x + 1);
if (vis[x - 1] == 0) {
vis[x] = 1;
dfs(x + 1);
vis[x] = 0;
}
}
int main() {
//freopen("in.txt", "r", stdin);
ios_base::sync_with_stdio(false), cin.tie(0), cout.tie(0);
for (int i = 0; i <= 30; ++i)vis[i] = 0;
dfs(1); cout << cnt << endl;
}
//2178309
2017磁砖样式
小明家的一面装饰墙原来是 3*10 的小方格。
现在手头有一批刚好能盖住2个小方格的长方形瓷砖。
瓷砖只有两种颜色:黄色和橙色。
小明想知道,对于这么简陋的原料,可以贴出多少种不同的花样来。
小明有个小小的强迫症:忍受不了任何2*2的小格子是同一种颜色。
(瓷砖不能切割,不能重叠,也不能只铺一部分。另外,只考虑组合图案,请忽略瓷砖的拼缝)
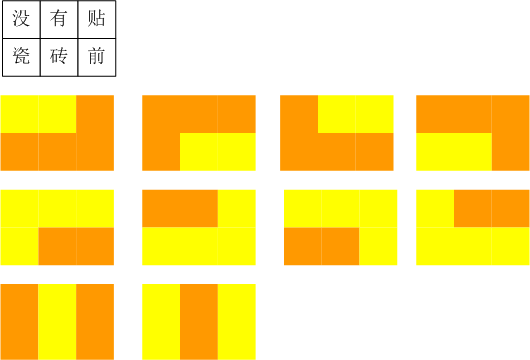
显然,对于 2*3 个小格子来说,口算都可以知道:一共10种贴法,如【p1.png所示】
但对于 3*10 的格子呢?肯定是个不小的数目,请你利用计算机的威力算出该数字。
注意:你需要提交的是一个整数,不要填写任何多余的内容(比如:说明性文字)
#include
using namespace std;
int n,m;
const int maxn = 10;
int g[maxn][maxn];
vector v;
set > se;
set > se2;
map Hash;
int ans = 0;
bool check_color() {
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++) {
if(i+1 <= n && j+1 <= m) {
//1 1 1 1 2 2 2 2 1 2 1 2
if((g[i][j]+g[i][j+1]+g[i+1][j]+g[i+1][j+1]) % 4 == 0)
return false;
}
}
return true;
}
bool check2(){
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(g[i][j] == 0){
return false;
}
}
}
for(int i=1;i<=n-1;i++){
for(int j=1;j<=m-1;j++){
int aa = g[i][j];
int bb = g[i+1][j];
int cc = g[i][j+1];
int dd = g[i+1][j+1];
if(aa == bb && aa ==cc && bb== cc && cc == dd && bb == dd && aa == dd){
return false;
}
}
}
return true;
}
bool check(){
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(g[i][j] == 0){
return false;
}
}
}
for(int i=1;i<=n-1;i++){
for(int j=1;j<=m-1;j++){
if(g[i][j] == g[i+1][j] == g[i][j+1] == g[i+1][j+1])
return false;
}
}
return true;
}
void dfs(int x,int y){
if(x == n+1 && y == 1){
// for(int i=1;i<=n;i++){
// for(int j=1;j<=m;j++){
// cout< >::iterator it = se2.begin();
vector vv;
while(it != se2.end()){
if(se2.find(*it) != se2.end() && se.find(*it) == se.end() ){
vv = *it;
break;
}
it++;
}
int t = 0;
for(int i=0;i 2016凑平方数
把0~9这10个数字,分成多个组,每个组恰好是一个平方数,这是能够办到的。 比如:0, 36, 5948721
再比如: 1098524736 1, 25, 6390784 0, 4, 289, 15376 等等…
注意,0可以作为独立的数字,但不能作为多位数字的开始。 分组时,必须用完所有的数字,不能重复,不能遗漏。
如果不计较小组内数据的先后顺序,请问有多少种不同的分组方案?
注意:需要提交的是一个整数,不要填写多余内容。
思路:
用到了STL里面的排列组合算法
next_permutation()返回的是一个布尔值,并且在内部已经把一个数组的顺序或者一个string的顺序改变了
然后利用set有去重的特性来插入
枚举所有可能的情况搜索即可
答案:300
#include
using namespace std;
typedef long long ll;
int arr[10] = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 };
ll nums[10];
set res;
//判断一个是否为平方数
bool isqnum(long long num) {
double d = sqrt(num);
return d == (long long)d;
}
//从arr:[i, n)寻找平方数
void dfs(int i, int n) {
if (i == 10) {
ll nums_t[10];
copy(nums, nums + n, nums_t);
sort(nums_t, nums_t + n);
string s;
for (int j = 0; j < n; ++j) {
s += to_string(nums_t[j]) + ',';
}
res.insert(s);
return;
}
if (arr[i] == 0) {
nums[n] = 0;
dfs(i + 1, n + 1);
return;
}
long long num = 0;
for (int j = i; j < 10; ++j) {
num = num * 10 + arr[j];
if (isqnum(num)) {
nums[n] = num;
dfs(j + 1, n + 1);
}
}
}
int main() {
do {
dfs(0, 0);
} while (next_permutation(arr, arr + 10));
cout << res.size() << endl;
return 0;
}
2015完美正方形
#include
using namespace std;
int n = 47 + 46 + 61;//边长
int a[19] = { 2, 5, 9, 11, 16, 17, 19, 21, 22, 24, 26, 30, 31, 33, 35, 36, 41, 50, 52 };
int g[500][500];//大正方形地图
int vis[30];
set se;//集合存储正方形最后一行边长数据结果
void fill(int x, int y, int l, int num) {
for (int i = x; i <= x + l - 1; i++) {
for (int j = y; j <= y + l - 1; j++) {
g[i][j] = num;
}
}
}
bool ok(int x, int y, int l) {
if (x + l - 1 > n) return false;
if (y + l - 1 > n) return false;
for (int i = x; i <= x + l - 1; i++) {
for (int j = y; j <= y + l - 1; j++) {
if (g[i][j] != 0) return false;
}
}
return true;
}
bool check() {
return true;
}
void dfs(int x, int y) {
if (x == n + 1) {//递归出口
if (check()) {
for (int i = 1; i <= n; i++) {
se.insert(g[n][i]);//set集合存储最后一层正方形边长数据
}
}
return;
}
if (g[x][y] != 0) {//当前正方形填充过了
if (y == n)
dfs(x + 1, 1);//dfs下一个
else
dfs(x, y + 1);//dfs下一个
}
else {//当前正方形没有填充过
for (int i = 0; i < 19; i++) {//枚举19块正方形
if (!vis[i]) {
if (ok(x, y, a[i])) {
fill(x, y, a[i], a[i]);//填充正方形成a[i]边长 以(x,y)为左上顶点
vis[i] = 1;
if (y == n) {
dfs(x + 1, 1);//dfs下一个
}
else {
dfs(x, y + 1);//dfs下一个
}
vis[i] = 0;//回溯
fill(x, y, a[i], 0);//填充正方形成0 以(x,y)为左上顶点
}
else {
break;//剪枝 因为a数组按顺序排的 当前边长不行 后面边长更不行了
}
}
}
}
}
int main() {
fill(1, 1, 47, 47);//填充以(1,1)为左上顶点的正方形 边为47
fill(1, 47 + 1, 46, 46);
fill(1, 47 + 46 + 1, 61, 61);
dfs(1, 1);//从(1,1)点开始搜索
set::iterator it = se.begin();
while (it != se.end()) {
cout << *it << " ";
it++;
}
return 0;
}
//30 33 41 50