数字通信理论在空时编码估计中的应用

多入多出技术(Multiple- Input Multiple- Output, MIMO)是无线通信领域技术上的重大突破。该技术能在不增加带宽的情况下成倍地提高通信系统的容量和频谱利用率，突破了香农容量的界限，使无线传输的容量达到有线传输的水平成为可能，成为下一代无线通信系统研究的热点问题之一。为了在信息传输中充分利用和尽可能接近无线MIMO系统的信道容量，人们很自然地将SISO系统中已比较成熟的各种编码技术推广到MIMO系统，因而空时编码应运而生。由于空时编码通过在不同天线发送的信号间引入了时域和空域相关，因此，能较好地利用由多发送多接收天线构成的MIMO系统所提供的传输分集度和自由度，可在不增加带宽和发送功率的情况下提高信息传输速率，改善信息传输性能。

下面，我来介绍下数字通信理论在空时分组码估计中的应用。空时分组码(STBC，Space-Time Block Codes)将无线MIMO系统中调制器输出的一定数目的符号编码为一个空时码码字矩阵，合理设计的空时分组码除能提供一定的发送分集度。STBC通常可通过对输入符号进行复数域中的线性处理而完成，因此，利用这一“线性"性质，采用低复杂度的检测方法就能检测出发送符号。特别是当STBC的码字矩阵满足正交设计时，例如Alamouti于1998年提出的两发射天线的发射分集方案，该方案在接收端采用的就是线性复杂度的最大似然(ML，Maximum likelihood)译码。

在空时分组码的估计中，最大似然算法这一思想被广泛应用。最大似然就是根据接收到的码字信息，构造发射的码字与接收码字之间关系的似然函数，在所有的可能的发射码字中，能使似然函数最大的那个码字即为发射所用的码字。

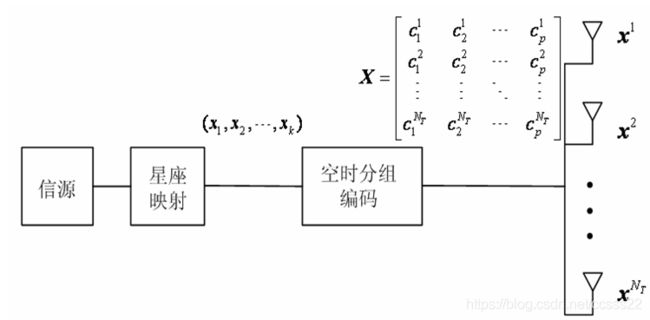
我们假设在接收端能确切知道信道状态信息(CSI，Channel state information)。正交空时分组码由于其较低的译码复杂度而在3G中应用比较广泛，下面我就简单介绍下正交空时分组码的估计。1999年Tarokh等人应用广义正交设计理论将Alamouti空时分组码推广到发射天线数N>2的情况，并将此类码字取名为正交空时分组码(OSTBC)。下图给出了空时分组码编码器示意图。

下面是我基于Alamouti最大似然译码算法而编写的MATLAB仿真程序：

clear;

clc;

mayuan=[0,1,1,0];%给定码元

l=length(mayuan);

qpsk_sequence=zeros(1,l/2);%QPSK调制

for k=1:l/2

        bit_to_transform = mayuan(2*k-1:2*k);

        if bit_to_transform == [0 0]

            qpsk_sequence(k) = 1/sqrt(2)*(-1-j);

        end

        if bit_to_transform == [1 0]

            qpsk_sequence(k) = 1/sqrt(2)*(1-j);

        end

        if bit_to_transform == [1 1]

            qpsk_sequence(k) = 1/sqrt(2)*(1+j);

        end

        if bit_to_transform == [0 1]

            qpsk_sequence(k) = 1/sqrt(2)*(-1+j);

        end

end

X=[qpsk_sequence(1) conj(qpsk_sequence(2));

qpsk_sequence(2)  conj(qpsk_sequence(1))];

H=zeros(1,2);%瑞利衰落信道模型的建立

R=eye(1*2);

Y=randn(1*2,1)/sqrt(2)+j*randn(1*2,1)/sqrt(2);

H=reshape(R'*Y,1,2)

R=H*X+randn(size(H*X));%接收模型的建立

y0=conj(H(1))*R(1)+H(2)*conj(R(2));

y1=conj(H(2))*R(1)-H(1)*conj(R(2));

s=[1/sqrt(2)*(-1-j) 1/sqrt(2)*(1-j) 1/sqrt(2)*(1+j) 1/sqrt(2)*(-1+j)];

cqpsk_sequence=zeros(1,l/2);%估计序列

c=zeros(1,length(s));

e=1;

for m=1:length(s)%遍历所有可能的发射信号与接收信号的欧氏距离（似然函数的构建）

    c(e)=(abs(s(e)-y0)).^2;

    c(m)=(abs(s(m)-y0)).^2;

     if c(m)

         e=m;

     end        

end

cqpsk_sequence(1)=s(e);

d=zeros(1,length(s));

f=1;

for n=1:length(s)

    d(f)=(abs(s(f)-y1)).^2;

    d(n)=(abs(s(n)-y1)).^2;

     if d(n)

         f=n;

     end

end

cqpsk_sequence(2)=s(f);

qpsk_sequence%发射码字

cqpsk_sequence%估计码字

仿真结果为：

qpsk_sequence =

  -0.7071 + 0.707i   0.7071 - 0.707i

cqpsk_sequence =

-0.7071 + 0.707i   0.7071 - 0.707i

其中qpsk_sequence为发射码字，cqpsk_sequence为估计码字。从中可以看出，最大似然算法能正确估计Alamouti发射方案的发射码字。

在上面的译码中，我们假设接收端能够正确识别调制方式。其实调制识别也不是一件很容易的事情，尤其是盲识别。就目前来讲，数字信号的调制识别所应用的理论工具多种多样，如时频分析理论、小波分析理论、基于似然比检测的调制分类、基于分形、混沌理论的调制识别等等。但是，目前还没一种能完全识别各种信号的大而全的方法。毕竟不同的调制方式特点不同，目前没有一种方法能够描述全部的调制方式。因此调制识别的方法也是多种多样的。此外，目前的各类算法，有的局限性很强，有些局限性小但复杂，运算量大，不适合信号的实时处理。因此需要综合应用各种算法，发挥其优点，尽量抑制其不足，探索新的适用范围广、算法简单、易于计算的调制识别算法。在信号的调制识别方面，还有很多科研工作需要继续。

当然，数字通信理论在空时编码估计中的应用还有很多，我这里只是简单是介绍了下其译码和调制理论的应用。在以后的学习中，数字通信理论还可能会贯穿到我研究方向（空时编码估计）的各个小的领域中，我一定要把这么课程学好学扎实。