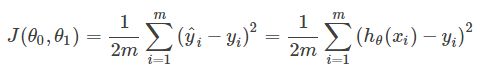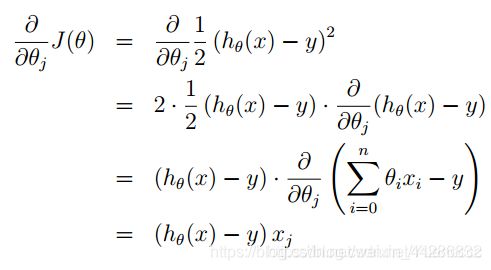基于矩阵向量的单变量线性回归（python实现 ）

基于矩阵向量的单变量线性回归（python实现 ）

梯度下降法实现

在本部分的练习中，我们将使用一个变量实现线性回归。我们需要找到城市人口数量与城市餐饮利润之间的关系，然后根据城市人口数量来预测城市餐饮的利润。数据集
链接：https://pan.baidu.com/s/1Zkdtsgvan8-YhwATFcBbSw
提取码：ABi8

导入用到的模块以及数据，进行可视化

#导入用到的模块
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d #mpl_toolkits.mplot3d是matplotlib中提供的专门画三维图的工具包
from mpl_toolkits.mplot3d import Axes3D #导入Axes3D用以创建三维图

#导入数据，进行数据的可视化
data = pd.read_csv('ex1data1.txt',names=['population','profit'])#当数据与py文件在同一目录下，可以直接用文件名导入数据
data.plot.scatter( 'population','profit',c='r',label='population')#可以使用列名进行数据读取
plt.title('Training Set')
plt.show()

数据可视化图

代价函数

(1)假设函数：H_θ（x）=θ₀+θ₁ ∗ x₁
我们增加一个虚拟的输入特征x₀ = （x₀₁ = 1，x₀₂ = 1，…x_0n = 1）， n∈N,此时H_θ（x）= θ^Tx
我们的目的是求出θ0，θ1的值，使得代价函数可以取最小值。
(2) 代价函数

代价函数

将其转化为矩阵向量的形式 =

#定义代价函数
def costFunction(X,y,theta):
    inner = np.power(X*theta.T - y,2)#np.power(a,3)就是a的立方
    return np.sum(inner)/(2*len(X))

梯度下降

梯度下降是一种用来求代价函数最小值的一种算法。

重复计算这个公式，直到函数收敛。（注意更新值θ应同时更新）
其中的α称之为步长，在最优化课中我们可以调整α的值。
这个α如果过小，则收敛很慢； 如果过大，则可能导致不收敛。

对于J(θ)的偏导数学推导过程如下：

其中x是向量，x_j是特征向量x中的第j元素。

#定义梯度下降函数
def gradientDescent(X,y,theta,alpha,iters):
    costs =[]
    for i in range(iters):
        wucha= (X*theta.T - y)
        theta -= (wucha.T*X)*alpha/len(X)  # theta.T代表矩阵的转置
        cost = costFunction(X,y,theta)
        costs.append(cost)
##      if i %100==0:   没迭代一百次输出一个cost
##         print(cost)
    return  theta,costs

完整代码实现

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d #mpl_toolkits.mplot3d是matplotlib中提供的专门画三维图的工具包
from mpl_toolkits.mplot3d import Axes3D #导入Axes3D用以创建三维图

# 导入数据pandas
data = pd.read_csv('ex1data1.txt',names=['population','profit'])#names是添加列名
data.plot.scatter( 'population','profit',c='r',label='population')
plt.title('Training Set')
plt.show()

#数据处理
data.insert(0,'ones',1)#对x要插入一列，列名为ones。值全部是一
X = data.iloc[:,0:2]#0列和1列所有元素，不包括第二列，或者2变为-1，代表最后一列（有两个冒号），也取不到
##cols=data.shape[1]  显示data的列数。.[0]是行数,或者用这个cols-1来切片
y = data.iloc[:,2:]#或者[:,-1]只有一个冒号就是所有行最后一列，因为第二列就是最后一列，所以：后边可以省略一个数字但是此时需要.reshape(9)
##print(len(X))输出X的样本数。使用[:,-1]是一维元组，此时需要y=y.values然后y=y.reshape(97,1)改为二维

##当使用-1的时候
##y = data.iloc[:,-1]
##y=y.values
##y=y.reshape(97,1)
##print(y.shape)


#将数据X,Y的数据结构（dataframe）转换为数组（ndarray）
X = np.matrix(X.values) #把X与Y转换为矩阵，方便接下来的矩阵操作X.values转换为array的形式。
y = np.matrix(y.values) #matrix的优势就是相对简单的运算符号，比如两个矩阵相乘，就是用符号*，但是array相乘不能这么用，得用方法.dot()
#print(y.shape) 检查X,y的维度


#定义代价函数
def costFunction(X,y,theta):
    inner = np.power(X*theta.T - y,2)#np.power(a,3)就是a的立方
    return np.sum(inner)/(2*len(X))

theta =np.zeros((1,2))#或者用这个theta = np.matrix(np.array([0,0]))，都是生成1*2矩阵(代价函数theta有转置)，若没有转置使用np.zeros((2,1))
##cost_init=costFunction(X,y,theta)
##print(cost_init)    输出初始的代价函数值


#定义梯度下降函数
def gradientDescent(X,y,theta,alpha,iters):
    costs =[]
   
    for i in range(iters):
        wucha= (X*theta.T - y)
        theta -= (wucha.T*X)*alpha/len(X)
        cost = costFunction(X,y,theta)
        costs.append(cost)
##      if i %100==0:   没迭代一百次输出一个cost
####        print(cost)
    return  theta,costs


alpha = 0.02
iters=2000
theta,costs=gradientDescent(X,y,theta,alpha,iters)

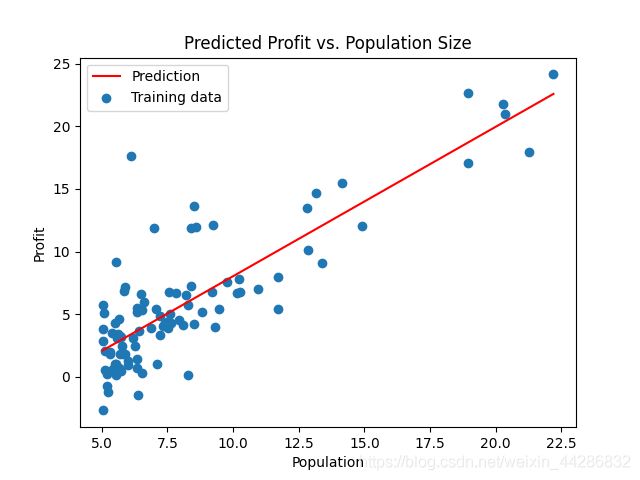
#  画线性拟合后的图形
##plt.figure() #创建画布
##plt.subplot(1,2,1)   #一行输出两个图形,且在第一个位置，画另一个图形时（1,2,2）则是同时输出两张图
x=np.linspace(X[:,-1].min(), X[:,-1].max(), 100) #抽X向量中100个样本，取样本可以直接切片X[:,1:]=X[:,-1]都是X最后一列
f=theta[0,0] + (theta[0,1]*x) 
plt.plot(x,f,'r',label='Prediction',)
plt.scatter(X[:,1:2].tolist(),y.tolist(),label='Training data')  #画散点图的时候，X,和y都是多维的，用.tolist改成一维
plt.xlabel('Population')
plt.ylabel('Profit')
plt.legend(loc=2)#显示标签位置
plt.title('Predicted Profit vs. Population Size')
plt.show()

#输出迭代次数与代价函数的变化
plt.plot(np.arange(iters),costs,label='cost vs iters')
plt.xlabel('iters')
plt.ylabel('cost')
plt.title('cost vs iters')
plt.legend(loc=1)
plt.show()
print(theta,costs[-1])


# 代价函数三维图
def CostContour(X,y):
    J_vals = np.zeros((100,100))
    theta0_vals = np.linspace(-10,10,100)
    theta1_vals = np.linspace(-1,4,100)
    for i in range(len(theta0_vals)):
        for j in  range(len(theta1_vals)):
            z = np.matrix((theta0_vals[i],theta1_vals[j]))
            J_vals[i,j] = costFunction(X,y,z)
    return theta0_vals,theta1_vals,J_vals


#绘制三维图        
fig=plt.figure()	
ax=Axes3D(fig)   #为创建的图片窗口添加一个类型为3D的图片，命名为ax
a,b,c = CostContour(X,y)
ax.plot_surface(a,b,c,cmap="rainbow")#cmap="rainbow"代表彩虹色
ax.set_xlabel('theta_0')
ax.set_ylabel('theta_1')
ax.set_zlabel('J(w,b)')
plt.show()

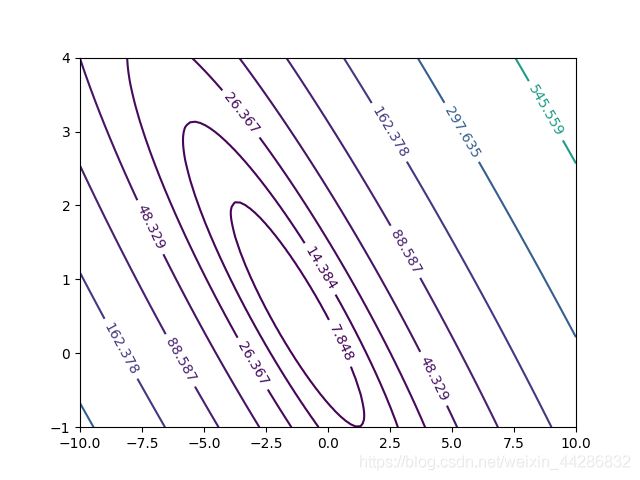
#绘制等高线图
plt.figure() #画等高线
lvls = np.logspace(-2, 3, 20) #以10**-2次方（0.01）和10**3（1000）之间的对数间隔绘制20条等高线。
a,_,c = CostContour(X,y)
_,b,_ = CostContour(X,y)
z = plt.contour(a,b,c,levels=lvls)
plt.clabel(z)  #显示每条等高线的代价函数值
plt.show() #显示图像

运行结果如下图所示

离散数据可视化

线性拟合图形

代价函数三维图

等高线图