Timus 1018. A Binary Apple Tree

Timus 1018. A Binary Apple Tree 要求给一棵苹果树剪枝，使其剩余的苹果最多。

---

1018. A Binary Apple Tree

Time Limit: 1.0 second
Memory Limit: 16 MB

Let's imagine how apple tree looks in binary computer world. You're right, it looks just like a binary tree, i.e. any biparous branch splits up to exactly two new branches. We will enumerate by natural numbers the root of binary apple tree, points of branching and the ends of twigs. This way we may distinguish different branches by their ending points. We will assume that root of tree always is numbered by 1 and all numbers used for enumerating are numbered in range from 1 to N, where N is the total number of all enumerated points. For instance in the picture below N is equal to 5. Here is an example of an enumerated tree with four branches:

2 5

 \ / 

 3 4

 \ /

 1

As you may know it's not convenient to pick an apples from a tree when there are too much of branches. That's why some of them should be removed from a tree. But you are interested in removing branches in the way of minimal loss of apples. So your are given amounts of apples on a branches and amount of branches that should be preserved. Your task is to determine how many apples can remain on a tree after removing of excessive branches.

Input

First line of input contains two numbers: N and Q (1 ≤ Q ≤ N; 1 < N ≤ 100). N denotes the number of enumerated points in a tree. Q denotes amount of branches that should be preserved. Next N−1 lines contains descriptions of branches. Each description consists of a three integer numbers divided by spaces. The first two of them define branch by it's ending points. The third number defines the number of apples on this branch. You may assume that no branch contains more than 30000 apples.

Output

Output should contain the only number — amount of apples that can be preserved. And don't forget to preserve tree's root ;-)

Sample

input	output
5 2 1 3 1 1 4 10 2 3 20 3 5 20	21

Problem Source: Ural State University Internal Contest '99 #2

---

这道题目是说，我们有一颗苹果树，该苹果树除了叶子节点以外的每个节点都分为两枝。每个节点使用 1 到 N 进行编号，其中根节点的编号为 1。每一枝上有若干苹果。为了方便采摘苹果，现在我们要对该苹果进行剪枝，要求剪去指定数目的枝条后，使被剪去的苹果数量最少。我们的任务就是求剪枝后该苹果树上还剩下多少个苹果。

输入的第一行包含两个数：N 和 Q (1 ≤ Q ≤ N; 1 < N ≤ 100)。 N 代表苹果树的节点数。Q 代表剪枝后该苹果树上还剩下多少树枝。剩下的 N−1 行用于描述树枝。每行包含三个整数。头两个整数代表节点编号，第三个整数代表该树枝上的苹果的数目。

输出只包含一个数，表示剪枝后该苹果树上还剩下的苹果的数目。注意，剪树时要保留该苹果树的根。

在程序中第 39 到 59 行的 Read 方法读取输入。

第 61 到 80 行的 Build 方法使用广度优先搜索算法读取的输入以建立苹果树。

第 82 到 94 行的 Solve 方法使用动态规划算法来计算剪枝后的苹果树上还剩下多少苹果。注意题目中允许 Q 的最大值为 N，实际 Q 的最大值应该是 N - 1。所以第 93 行使用了 Math.Max 方法以处理 Q = N 的情况。

注意在程序中节点的编号改为从 0 到 N - 1。

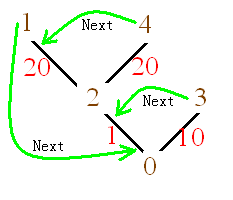
下面是用题目中所给的输入例子，程序运行时的状态：

Read:

0: To:2 Cnt: 1 Next:-1

1: To:0 Cnt: 1 Next:-1

2: To:3 Cnt:10 Next: 0

3: To:0 Cnt:10 Next:-1

4: To:2 Cnt:20 Next:-1

5: To:1 Cnt:20 Next: 1

6: To:4 Cnt:20 Next: 5

7: To:2 Cnt:20 Next:-1



Build:

0: sz:-1 edge: 0 kid:(3, 2) vec:2 qz:0

1: sz: 0 edge:20 kid:(0, 0) vec:4 qz:3

2: sz:-1 edge: 1 kid:(4, 1) vec:6 qz:2

3: sz: 0 edge:10 kid:(0, 0) vec:3 qz:4

4: sz: 0 edge:20 kid:(0, 0) vec:7 qz:1



Solve:

dp   0  1  2  3  4

0:  51 41 21 10  0  sz:4

1:   0  0  0  0  0  sz:0

2:  40 20  0  0  0  sz:2

3:   0  0  0  0  0  sz:0

4:   0  0  0  0  0  sz:0

最后，源程序代码如下：

  1  using  System;
  2  using  System.IO;
  3 
  4  namespace  Skyiv.Ben.Timus
  5  {
  6     //   http://acm.timus.ru/problem.aspx?space=1 &num=1018
  7     sealed   class  T1018
  8    {
  9       struct  Element
 10      {
 11         int  to, cnt, next;
 12        
 13         public   int  To {  get  {  return  to; } }
 14         public   int  Cnt {  get  {  return  cnt; } }
 15         public   int  Next {  get  {  return  next; } }
 16        
 17         public  Element( int  to,  int  cnt,  int  next)
 18        {
 19           this .to  =  to;
 20           this .cnt  =  cnt;
 21           this .next  =  next;
 22        }
 23      }
 24      
 25       static   void  Main()
 26      {
 27         new  T1018().Run(Console.In, Console.Out);
 28      }
 29      
 30       void  Run(TextReader reader, TextWriter writer)
 31      {
 32        Element[] buf;
 33         int [] vec, sz, edge;
 34        var q  =  Read(reader,  out  vec,  out  buf);
 35        var kid  =  Build(vec, buf,  out  sz,  out  edge);
 36        writer.WriteLine(Solve(q, kid, sz, edge));
 37      }
 38      
 39       int  Read(TextReader reader,  out   int [] vec,  out  Element[] buf)
 40      {
 41        var ss  =  reader.ReadLine().Split();
 42        var n  =   int .Parse(ss[ 0 ]);
 43        var q  =   int .Parse(ss[ 1 ]);
 44        buf  =   new  Element[(n  -   1 )  *   2 ];
 45        vec  =   new   int [n];
 46         for  (var i  =   0 ; i  <  n; i ++ ) vec[i]  =   - 1 ;
 47         for  ( int  k  =   0 , i  =   1 ; i  <  n; i ++ )
 48        {
 49          ss  =  reader.ReadLine().Split();
 50          var a  =   int .Parse(ss[ 0 ])  -   1 ;
 51          var b  =   int .Parse(ss[ 1 ])  -   1 ;
 52          var cnt  =   int .Parse(ss[ 2 ]);
 53          buf[k]  =   new  Element(b, cnt, vec[a]);
 54          vec[a]  =  k ++ ;
 55          buf[k]  =   new  Element(a, cnt, vec[b]);
 56          vec[b]  =  k ++ ;
 57        }
 58         return  q;
 59      }
 60      
 61       int [,] Build( int [] vec, Element[] buf,  out   int [] sz,  out   int [] edge)
 62      {
 63        var kid  =   new   int [vec.Length,  2 ];
 64        var qz  =   new   int [vec.Length];
 65        sz  =   new   int [vec.Length];
 66        edge  =   new   int [vec.Length];
 67         for  ( int  k  =   1 , n  =   0 , i  =   0 ; i  <  k; i ++ , n  =   0 )
 68        {
 69          sz[qz[i]]  =   - 1 ;
 70           for  (var j  =  vec[qz[i]]; j  !=   - 1 ; j  =  buf[j].Next)
 71          {
 72             if  (sz[buf[j].To]  ==   - 1 )  continue ;
 73            kid[qz[i], n ++ ]  =  buf[j].To;
 74            edge[buf[j].To]  =  buf[j].Cnt;
 75            qz[k ++ ]  =  buf[j].To;
 76          }
 77           if  (n  ==   0 ) sz[qz[i]]  =   0 ;
 78        }
 79         return  kid;
 80      }
 81      
 82       int  Solve( int  q,  int [,] kid,  int [] sz,  int [] edge)
 83      {
 84        var dp  =   new   int [sz.Length, sz.Length];
 85         for  (var c  =  sz.Length  -   1 ; c  >=   0 ; c -- )
 86        {
 87           if  (sz[c]  ==   0 )  continue ;
 88          sz[c]  =  sz[kid[c,  0 ]]  +  sz[kid[c,  1 ]]  +   2 ;
 89          Do(dp, kid, sz, edge, c,  0 );
 90          Do(dp, kid, sz, edge, c,  1 );
 91          Do(dp, kid, sz, edge, c);
 92        }
 93         return  dp[ 0 , Math.Max( 0 , sz.Length  -   1   -  q)];
 94      }
 95      
 96       void  Do( int [,] dp,  int [,] kid,  int [] sz,  int [] edge,  int  c,  int  k)
 97      {
 98         for  (var i  =   0 ; i  <=  sz[kid[c, k]]; i ++ )
 99        {
100          var j  =  i  +  sz[kid[c,  1   -  k]]  +   1 ;
101          var m  =  dp[kid[c, k], i]  +  edge[kid[c, k]];
102           if  (dp[c, j]  <  m) dp[c, j]  =  m;
103        }
104      }
105 
106       void  Do( int [,] dp,  int [,] kid,  int [] sz,  int [] edge,  int  c)
107      {
108         for  (var i  =   0 ; i  <=  sz[kid[c,  0 ]]; i ++ )
109           for  (var j  =   0 ; j  <=  sz[kid[c,  1 ]]; j ++ )
110          {
111            var m  =  dp[kid[c,  0 ], i]  +  dp[kid[c,  1 ], j]  +  edge[kid[c,  0 ]]  +  edge[kid[c,  1 ]];
112             if  (dp[c, i  +  j]  <  m) dp[c, i  +  j]  =  m;
113          }
114      }
115    }
116  }

 

---

返回目录