递归之八皇后

前言：

　　对于接触过编程的朋友来说，最开始了解的算法莫过于贪心或者递归；而提到递归，除了本博文前面介绍的汉诺塔问题以外，还有一个比较有趣的问题——八皇后问题。现在就跟大家理一理，分享一下代码的实现思路。

1. 问题介绍：

八皇后问题指如何能够在 8×8 的国际象棋棋盘上放置八个皇后，使得任何一个皇后都无法直接吃掉其他的皇后？即任两个皇后都不能处于同一条横行、纵行或斜线上。

 

2. 问题分析：

Step1 数据结构选择

方案一：采用8*8二维数组存储棋盘board(x,y);

方案二：采用8*1一维数组存储棋盘每行放置的皇后位置q[i];

（为方便代码实现，这里采用一维数组进行存储）

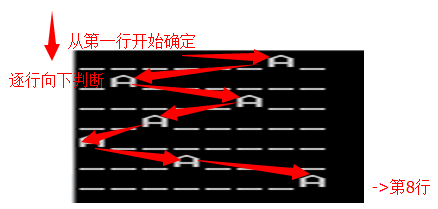
Step2 递归跳出边界

由于递归过程中，每一种符合的方案都必须遍历到最后一行，因此判断边界为”i==8”

Step3 放置皇后的向下递归规则

根据定义，“任两个皇后都不能处于同一条横行、纵行或斜线上”即

（1）q[i]唯一

（2）q[i]!=q[x](x=1,2...,i-1)

（3）abs(q[i]-y)!=abs(i-x)

 

3. 代码实现

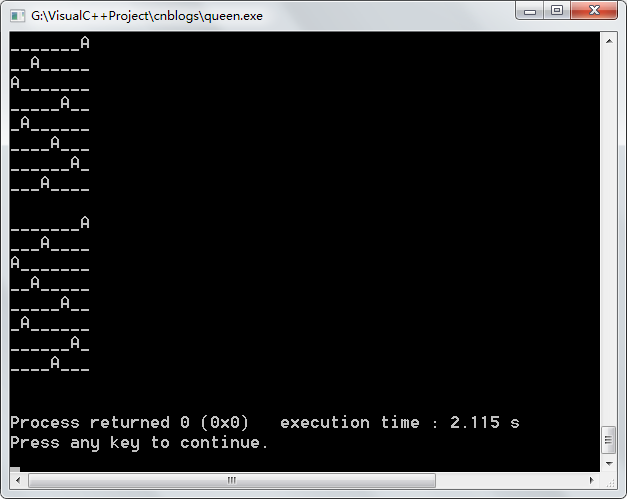
3.1列出满足八皇后问题的所有方案

 

 1 #include <cstdio>

 2 #include <cstring>

 3 #include <math.h>

 4 #define N 8

 5 int q[N];   //queen position in 8 rows

 6 //函数声明

 7 void pri();

 8 void dfs(int);

 9 void placeon(int ,int );

10 void takeout(int ,int );

11 int canplace(int ,int );

12 int main(){

13     dfs(0);

14     return 0;

15 }

16 //函数定义

17 void pri(){

18     for(int i=0;i<N;i++){

19         for(int j=0;j<N;j++){

20             if(q[i]==j) printf("A");

21             else printf("_");

22         }

23         printf("\n");

24     }

25     printf("\n");

26 }

27 void dfs(int x){

28     if(x==N){pri();}

29     else{

30 

31         for(int i=0;i<N;i++)if(canplace(x,i)){

32             placeon(x,i);

33             dfs(x+1);

34             takeout(x,i);

35         }

36     }

37 }

38 void placeon(int x,int y){q[x]=y;}

39 void takeout(int x,int y){q[x]=-1;}

40 int canplace(int x,int y){

41     for(int i=0;i<x;i++) if(q[i]==y || fabs(x-i)==fabs(y-q[i])){

42         return 0;

43     }

44     return 1;

45 }

 

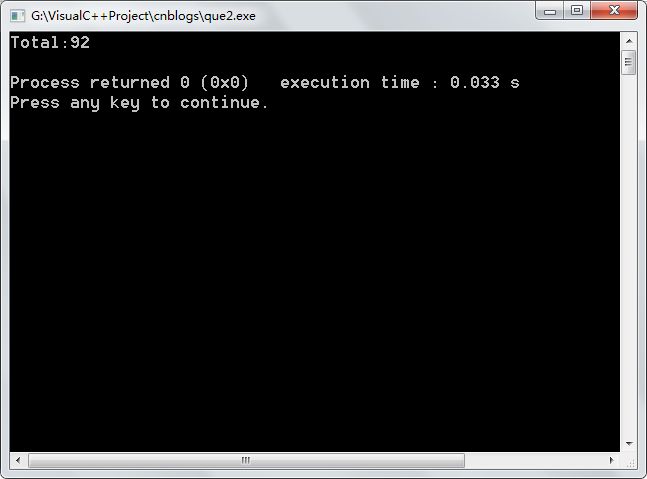
3.2计算总方案数（仅添加一全局变量）

 

 1 #include <cstdio>

 2 #include <cstring>

 3 #include <cmath>

 4 #define N 8

 5 int q[N];   //queen position in 8 rows

 6 int cnt=0;    //全局变量,方案总数

 7 //函数声明

 8 void dfs(int);

 9 void placeon(int ,int );

10 void takeout(int ,int );

11 int canplace(int ,int );

12 int main(){

13     dfs(0);

14     printf("Total:%d\n",cnt);

15     return 0;

16 }

17 //函数定义

18 void dfs(int x){

19     if(x==N){cnt++;}

20     else{

21         for(int i=0;i<N;i++)if(canplace(x,i)){

22             placeon(x,i);

23             dfs(x+1);

24             takeout(x,i);

25         }

26     }

27 }

28 void placeon(int x,int y){q[x]=y;}

29 void takeout(int x,int y){q[x]=-1;}

30 int canplace(int x,int y){

31     for(int i=0;i<x;i++) if(q[i]==y || fabs(x-i)==fabs(y-q[i])){

32         return 0;

33     }

34     return 1;

35 }

 

3.3结果展示：

 

 

结语：

关于八皇后问题，基于回朔的思想（简单讲就是枚举）利用递归的算法进行实现相当精巧。当然，本博文算法的实现其实应该还可以剪枝优化，只不过本人在此只是抛砖引玉，希望感兴趣的朋友后续自己进行尝试！