BundleFusion: Real-time GloballyConsistent 3D Reconstruction... 论文解析

1 概述

在BundleFusion之前的很多相似的方案中，在重建的过程中总是出现以下问题：

1. 需要额外的时间来纠正在线的错误，从而无法很好的实现实时处理
2. 十分脆弱的tracking方案，从而导致位姿估计出现错误
3. 扫描的结果试用点的形式在表示，限制了扫描的质量和适用性

BundleFunsion 从以下几个方面把上面的问题进行了解决：

1. 通过分级的方式，使得历史的所有帧，都参与了优化
2. 不再是短暂的tracking，而是全局的tracking
3. 设计了一个并行系统来进行优化。同时分别使用了稀疏的特征和稠密的光度特征和几何结构特征来实现匹配
4. 该方法实现了位姿全局实时的优化，同时tracking失败后也可以重新定位
5. 可以对已生成的3D模型进行新的估计

作者认为在三维重建中比较重要的一些要素：

1. 高质量的表面建模
2. 可伸缩性：因为需要同时处理小的和大的场景的扫描，同时保证全局结构和局部结构的精度
3. 全局建模的一致性：可以通过回环检测实现
4. 已经建好的模型可以根据实时的输入进行动态的更新
5. 实时的建模速率

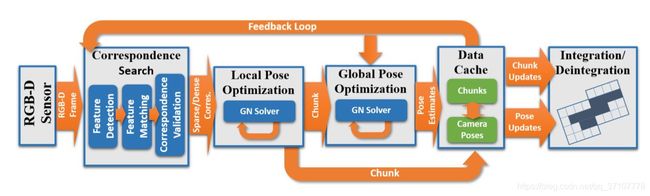
2 实现方法

首先概括的说一下本文的方法。

1. RGB-D相机作为输入
2. 为了实现全局的一致性，使用了由稀疏到稠密的全局位姿优化方案：首先试用检测到的稀疏的图像特征（SIFT）来进行粗糙的位姿优化，同时该稀疏的特征也可以用来进行回环检测和重定位。之后再用稠密的光度信息和几何信息来进一步优化
3. 通过设计滤波器来阻止误匹配的发生，也可以有效地防止错误的加入回环帧进行优化
4. 为了实现实时的全局位姿优化，设计了由局部到全局的优化方案：每n个连续帧，进行打包称为一个chunk，来进行局部的位姿优化；之后通过chunk之间的联系来进行全局的位姿优化
5. 利用并行的GPU来解决这个非线性优化的问题
6. 可以通过新的实时的de-integration 和 integration 对TSDF地图进行实时更新

3 Global pose aligenment

实时的RGB-D数据用$\text{S}$来表示，$\text{S}=\{f_i=\{C_i,D_i\}\}$，$C_i$代表$f_i$帧的颜色数据，$D_i$代表$f_i$帧的深度数据。采集数据的频率是30Hz，分辨率为 $640\times 480$。$T_i(\text{p})={\text{R}}_i\text{p}+{\text{t}}_i$是把在$f_i$坐标系的点$\text{p}$转到世界坐标系中。

3.1 Feature correspondence search

首先使用特征查找，特征匹配和correspondences滤波器，来查找稀疏的correspondences。本文使用的是SIFT，而且correspondences search全部是在GPU上进行处理，可以在0.05ms中查找一对图像的特征点。

3.1.2 Correspondence Filtering

Key Point Correspondence Filter
在$f_i$和$f_j$两帧之间在三维空间中有相互对应的correspondences points 集合 $P$ 和 $Q$。在此之前，经过位姿的优化求解（后面会介绍），已经获得了 $T_i$ 和 $T_j$ ，结合 Kabsch algorithm 来计算 $T_{ij}$（点从 $f_i$ 到 $f_j$ 的变换矩阵）。然后再求一下 $P_{cur}$ 和 $Q_{cur}$ 的 corss-covariance；如果值比较大（>100）那么证明该系统不稳定，需要进一步操作。如果一对特征点的重投影误差或者经过条件分析认为它不稳定，那么移除该对应的点。直到符合要求或者correspondences的个数不足以求$f_i$和$f_j$ 的变换才停止。如果最后还没有产生符合要求的$T_{ij}$，我们就把整个 $f_i$和$f_j$ 全部抛弃。

Surface area filter
把 $f_i$ 的 3D keypoints $P$ 和 $f_j$ 的 3D keypoints $Q$ 投影到相机平面上，再用 2D oriented bounding box 的方法来圈住这些点，求 bounding box 的面积，如果面积太小（$<0.032m^2$）则认为不够稳定，抛弃这些匹配。

Dense verification

为了效率考虑，在验证的时候，我们使用经过滤波且降采样的图片进行验证
$${\left|\left|T_{ij}({\text{p}}_{i,x,y})-{\text{q}}_{j,x,y}\right|\right|}_2<{\tau }_d(1)$$
$$(T_{ij}({\text{n}}_{i,x,y}))\cdot {\text{n}}_{j,x,y}>{\tau }_n(2)$$
$${\left|\left|C_i^{low}(x,y)-C_j^{low}(x,y)\right|\right|}_1<{\tau }_c(3)$$

$C_i^{low}$是经过降采样的color intensity，$D_i^{low}$是深度信息。$P_i^{low}$和$N_i^{low}$是$D_i^{low}$对应的位置信息和法向量。${\text{p}}_{i.x.y}=P_i^{low}(x,y)$并且$q_{i,x,y}=P_j^{low}({\pi }^{-1}(T_{ij}{\text{p}}_{i,x,y}))$。但是式(1)对于遮挡产生的错误十分敏感，所以我们抛弃有较大深度差异、法向量偏差或者缺少光度一致性的correspondences，从而得到了式(2)和(3)。如果这些检验都通过了的话，那么把correspondences加入有效集合。帧与帧之间至少需要3对correspondences，实验证明5个的话，效果更好。

3.2 Hierarchical optimization

在第一阶段，我们在一个chunk内优化位姿变换，第二阶段，优化chunk之间的位姿变换。

Local Intra-Chunk Pose Optimization

1. 把$N_{chunk}=11$连续帧作为一个chunk。因为每个chunk帧数很少且连续，所以变化不大，因此可以用单位矩阵来初始化transformation。
2. 为了保证局部位姿优化的准确度，我们在得到chunk内部初步优化过的trajectory后，使用Dense verification检测。
3. 如果重投影误差很大，那么整个chunk将会被抛弃。

Per-Chunk Keyframes
经过前面的处理之后，把每个chunk的第一个元素作为该chunk的keyframe。也计算一个chunk里面聚合的keyframe feature集合，即把chunk里面所有的特征点的坐标系变换到keyframe的坐标系，那些在三维空间中一致的点用最小二乘法优化到一个最佳的位置。因此一个chunk最终可以获得一帧即keyframe，里面包含统一的特征位置以及深度信息。

Global Inter-Chunk Pose Optimization

1. 稀疏的correspondence search 和 filtering和chunk内的操作一样。只不过这次在keyframe上操作
2. 如果在全局的keyframe上没有找到和以前相匹配的keyframes，那么该帧暂定为无效帧，放入候选名单，如果未来找到匹配的keyframes再使用
3. 全局的位姿优化计算keyframes位姿在全局范围内的一致性，可以把chunks在世界坐标系下进行校准。

3.3 Pose alignment as energy optimization
前面多次提到了位姿的优化和校准，那么本节将会介绍具体的方法。如果有一系列帧$S$，那么所有帧的参数向量是
$$\chi =({\text{R}}_0,{\text{t}}_0,\dots ,{\text{R}}_{|S|},{\text{t}}_{|S|}{)}^T=(x_0,\dots ,x_N{)}^T$$

其中${\text{R}}_i\in s{o}_3\in {\mathbb{R}}^3$
基于sparse features 和 dense photometric and geometric constraints的方程为：
$$E_{align}(\chi )={\omega }_{sparse}{E}_{sparse}(\chi )+{\omega }_{dense}{E}_{dense}(\chi )$$
${\omega }_{sparse}$和${\omega }_{dense}$是sparse和dense matching terms的权重。

Sparse matching
$$E_{sparse}(\chi )=\sum _{i=1}^{|S|}\sum _{j=1}^{|S|}\sum _{(k,l)\in \text{C}(i,j)}{\left|\left|T_i{\text{p}}_{i,k}-T_j{\text{p}}_{j,l}\right|\right|}_2^2$$
${\text{p}}_{i,k}$是第i帧第k个检测到的特征点，${\text{C}}_{i,j}$是第i帧和第j帧之间的匹配对。

Dense matching
$$E_{dense}(T)={\omega }_{photo}{E}_{photo}(T)+{\omega }_{geo}{E}_{geo}(T)$$
$$E_{photo}(\chi )=\sum _{(i,j)\in \text{E}}\sum _{k=0}^{|I_i|}{\left|\left|I_i(\pi ({\text{d}}_{i,k}))-I_j(\pi (T_j^{-1}{T}_i{\text{d}}_{i,k}))\right|\right|}_2^2$$
$$E_{geo}(\chi )=\sum _{(i,j)\in \text{E}}\sum _{k=0}^{|D_i|}{\left[{\text{n}}_{i,k}^T({\text{d}}_{i,k}-T_i^{-1}{T}_j{\pi }^{-1}(D_j(\pi (T_j^{-1}{T}_i{\text{d}}_{i,k}))))\right]}^2$$
这里$C_i$是颜色信息，$D_i$是深度信息，集合$\text{E}$包含的是相机角度相似，有交集的“帧对(frame pair)”$(i,j)$。${\omega }_{photo}$和${\omega }_{geo}$是对应的权重。$I_i$是$C_i$的亮度梯度，可以使得优化更鲁棒。

3.4 Fast and robust optimization strategy

该部分主要工作室完成以下方程的解：
$${\chi }^{\ast }=arg\underset{\chi }{\min }{E}_{align}(\chi )$$
本文采用了高斯牛顿法求解，过程不再赘述。

4 Dynamic 3D reconstruction

本文使用的是TSDF来建图，与以往不同的是，除了integration还考虑了de-integration
$$D^{\prime }(v)=\frac{D(v)W(v)+w_i(v)d_i(v)}{W(v)+w_i(v)},W^{\prime }(v)=W(v)+w_i(v)$$
$$D^{\prime }(v)=\frac{D(v)W(v)-w_i(v)d_i(v)}{W(v)-w_i(v)},W^{\prime }(v)=W(v)-w_i(v)$$