TensorFlow2.1（Anaconda）学习笔记五之单变量线性回归实践

本文内容基于深度学习应用开发-TensorFlow实践慕课教程。

示例

课程以y=2*x+1为例，人工生成数据集，构建、训练模型，最后进行预测。
下面是我在Anaconda上照猫画虎敲的代码：

import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline

x_data = np.linspace(-1,1,100)
np.random.seed(5)
y_data = 2 * x_data + 1 + np.random.randn(*x_data.shape) * 0.4#加入噪声
#画出散点图
plt.scatter(x_data,y_data)
plt.plot(x_data,2 * x_data + 1,color = 'red',linewidth=1)

#前向计算
def model(x,w,b):
    return tf.multiply(x,w)+b

#初始化参数w,b
w =tf.Variable(np.random.randn(),tf.float32)
b = tf.Variable(0.0,tf.float32)

#均方差损失函数(回归问题最常用的损失函数)
def loss(x,y,w,b):
    err = model(x,w,b) - y
    return tf.reduce_mean(tf.square(err))

#超参数设置的不同将直接导致结果的准确性。
epochs = 10
lr = 0.01

#计算梯度
def grad(x,y,w,b):
    with tf.GradientTape() as tape:
        loss_ = loss(x,y,w,b)
        return tape.gradient(loss_,[w,b])
    
#记录训练步数
step = 0
#保存loss值的列表
loss_list = []
#每隔多少步显示一次loss值
display_step = 40

for epoch in range(epochs):
    for xs,ys in zip(x_data,y_data):
        loss_ = loss(xs,ys,w,b)
        loss_list.append(loss_)
        delta_w,delta_b = grad(xs,ys,w,b)
        change_w = delta_w * lr#学习率乘以损失值loss对w的偏导，即w需要调整的值
        change_b = delta_b * lr
        w.assign_sub(change_w)# w减去其要调整的值同时赋值
        b.assign_sub(change_b)
        step = step + 1
        if step % display_step == 0:
            print("epoch:","%02d" % (epoch+1),"step:%03d" % (step),"loss=%.6f" % (loss_))
        #完成一轮训练后画出图像
        plt.plot(x_data,w.numpy() * x_data + b.numpy())

#输出最终的w,b的值
print("w=",w.numpy())
print("b=",b.numpy())

#结果可视化
plt.scatter(x_data,y_data,label="Original data")
plt.plot(x_data,x_data * 2 + 1,label="Object line",color="g",linewidth=3)
plt.plot(x_data,x_data * w.numpy() + b.numpy(),label="Fitted line",color="r",linewidth=3)
plt.legend(loc=2)

#损失可视化
plt.plot(loss_list,linewidth=1)

#预测
x_test = 3.21
pred = model(x_test,w.numpy(),b.numpy())
target = 2 * x_test + 1
print("x={},预测值为{:.6f},真实值为{:.6f}".format(x_test,pred,target))

总体来看，预测的结果还是很准确的。

测验

下面的课程的小作业：
通过生成人工数据集合，基于TensorFlow实现y=3.1234x+2.98线性回归。
1、生成 x_data，值为 [0, 100]之间500个等差数列数据集合作为样本特征根据目标线性方程 y=3.1234x+2.98，生成相应的标签集合 y_data；
2、画出随机生成数据的散点图和想要通过学习得到的目标线性函数y=3.1234*x+2.98；
3、构建回归模型；
4、训练模型，10轮，每训练20个样本显示损失值；
5、通过训练出的模型预测 x=5.79 时 y 的值，并显示根据目标方程显示的 y 值；
6、通过Tensorboard显示构建的计算图。

第六步因为我不会，所以只完成了前五步。

import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline

x_data = np.linspace(0,100,500)
np.random.seed(5)
y_data = 3.1234 * x_data + 2.98 + np.random.randn(*x_data.shape) * 0.1
#画出散点图
plt.scatter(x_data,y_data)
plt.plot(x_data,3.1234 * x_data + 2.98,color = 'red',linewidth=1)

#前向计算
def model(x,w,b):
    return tf.multiply(x,w)+b

#初始化参数w,b
w =tf.Variable(np.random.randn(),tf.float32)
b = tf.Variable(0.0,tf.float32)

#自定义损失函数，注意，我这里不使用均方差，因为存在平方会使loss过大，最后导致loss值为nan，这里采用绝对值计算预测值和实际值间的损失。
def loss(x,y,w,b):
    err = model(x,w,b) - y
    return tf.reduce_mean(abs(err))
'''
def loss(x,y,w,b):
    err = model(x,w,b) - y
    return tf.reduce_mean(tf.square(err))
'''
epochs = 10
lr = 0.00009

#计算梯度
def grad(x,y,w,b):
    with tf.GradientTape() as tape:
        loss_ = loss(x,y,w,b)
        return tape.gradient(loss_,[w,b])
    
#记录训练步数
step = 0
#保存loss值的列表
loss_list = []
#每隔多少步显示一次loss值
display_step = 20

for epoch in range(epochs):
    for xs,ys in zip(x_data,y_data):
        loss_ = loss(xs,ys,w,b)
        loss_list.append(loss_)
        delta_w,delta_b = grad(xs,ys,w,b)
        change_w = delta_w * lr#学习率乘以损失值loss对w的偏导，即w需要调整的值
        change_b = delta_b * lr
        w.assign_sub(change_w)# w减去其要调整的值同时赋值
        b.assign_sub(change_b)
        step = step + 1
        if step % display_step == 0:
            print("epoch:","%02d" % (epoch+1),"step:%03d" % (step),"loss=%.6f" % (loss_))
        #完成一轮训练后画出图像
        plt.plot(x_data,w.numpy() * x_data + b.numpy())

#输出最终的w,b的值
print("w=",w.numpy())
print("b=",b.numpy())

#结果可视化
plt.scatter(x_data,y_data,label="Original data")
plt.plot(x_data,x_data * 3.1234 + 2.98,label="Object line",color="g",linewidth=3)
plt.plot(x_data,x_data * w.numpy() + b.numpy(),label="Fitted line",color="r",linewidth=3)
plt.legend(loc=2)

#损失可视化
plt.plot(loss_list,linewidth=1)

#预测
x_test = 5.79
pred = model(x_test,w.numpy(),b.numpy())
target = 3.1234 * x_test + 2.98
print("x={},预测值为{:.6f},真实值为{:.6f}".format(x_test,pred,target))

总结与反思
结果差强人意吧，从图像上看基本和原函数重合了。但是b的值相差的有点大了。当x稍微大一点预测得还是比较准的（测验要求x=5.79正好碰到了我的软肋）
在做这道题时，我原以为把示例y=2*x+1中的2和1分别改成3.1234和2.98就行了，没想到碰到了loss值突增以至于后面为nan的情况。
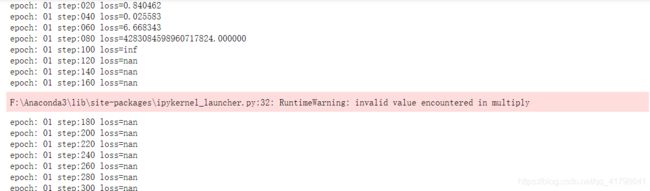我想了想可能是因为损失函数中有平方操作所致，因为示例中x范围是-1到1而测验是0到100，于是我把平方改成了绝对值便解决了这个问题。其实我还想到了一种方法，归一化。不知道有没有用，具体怎么操作我现在还不清楚。

进一步改进：

将数据进行归一化，将损失函数恢复成均方差损失函数。
画出计算图。
归一化公式：newValue = (oldValue - min) / (max - min)
变更处如下：

import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline

x_data = np.linspace(0,100,500)
np.random.seed(5)

#数据归一化
for i in range(500):
    x_data[i]=(x_data[i]-min(x_data))/(max(x_data)-min(x_data))

y_data = 3.1234 * x_data + 2.98 + np.random.randn(*x_data.shape) * 0.3
#画出散点图
plt.scatter(x_data,y_data)
plt.plot(x_data,3.1234 * x_data + 2.98,color = 'red',linewidth=1)

#均方差损失函数
def loss(x,y,w,b):
    err = model(x,w,b) - y
    return tf.reduce_mean(tf.square(err))

epochs = 10
lr = 0.05

经过修正，再次运行，w和b的值已经比较接近正确值了。

再次总结

归一化果然有用。
在优化器不变和损失函数不变的情况下，函数的拟合结果（w,b的值）比较大的除了和两个超参数(学习率和训练轮数)有关外应该还和w,b的初始值有关，最开始w是随机数初始化，b是0，现在我把他们都设置成了3。
因为还没找到计算图先关的教程，所以我现在还不会生成计算图。