西电研一人工智能复习随笔

记：人工智能和先进人工智能写在一起了,懒得分开写

第一章

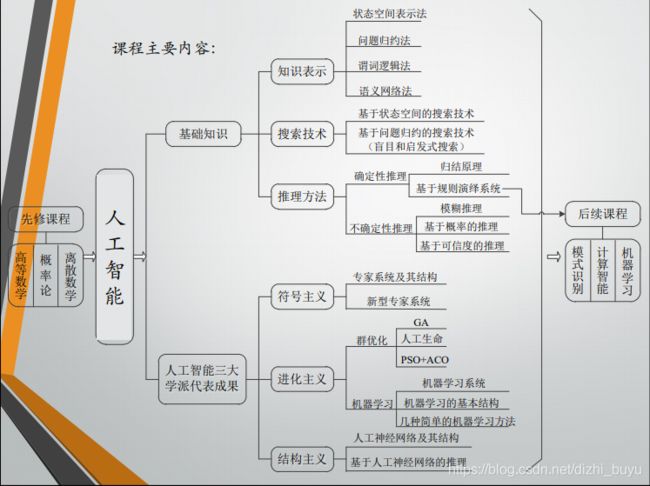
先说总体框架：人工智能

先给几个概念

Artificial Intelligence (AI)：人工智能就是用人工的方法在机器（计算机）上实现的智能，或称机器智能、计算机智能。

知识：人们通过体验、学习或联想而知晓的对客观世界规律性的认识，包括事实、条件、过程、规则、关系和规律等。

智能：一种应用知识对一定环境或问题进行处理的能力或者进行抽象思考的能力。

需要了解一下 符号主义 连接主义 行为主义 三者的特点和区分：(好家伙,愣是看不出来这块想考啥)

符号主义：

• 原理：物理符号系统假设和有限合理性原理
• 立足于逻辑运算和符号操作,适合于模拟人的逻辑思维过程,解决需要逻辑推理的复杂问题
• 功能模拟方法：模拟人类认知系统所具备的功能，通过数学逻辑方法来实现人工智能

连接主义

• 原理：神经网络及神经网络间的连接机制与学习算法
• 通过神经元之间的并行协作实现信息处理,处理过程具有并行性,动态性,全局性
• 模拟人的生理神经网络结构，不同的结构表现出不同的功能和行为。认为功能、结构和智能行为是不可分的。

行为主义

• 原理：控制论及感知—动作型控制系统
• 采用行为模拟方法，也认为功能、结构和智能行为是不可分的。不同行为表现出不同功能和不同控制结构。

第二章 知识表示方法

了解知识表示,并熟悉几种知识表示的常用方法

知识表示

相关概念(了解即可)

• 一般来说，我们把有关信息关联在一起所形成的信息结构称为知识。
• 知识表示就是对知识的一种描述，一种计算机可以接受的用于描述知识的数据结构。
• 知识的要素：指构成知识的必需元素。一般而言，人工智能系统的知识包含事实、规则、控制和元知识。

知识表示方法

状态空间法

基本要素：基于解答空间的问题表示和求解方法就是状态空间法

• 状态（State）：为描述某类不同事物间的差别而 入的一组最少变量 q0 q1，…，qn的有序集合 
  给定每个分量的一组值就得到一个具体的状态，例如Qk =[q０k, , q1k ,…,qnk ] 表示一个具体的状态
• 算符（operator）：把问题从一种状态变换为另一种状态的手段
  算符可为走步、过程、规则、数学算子、运算符号 或逻辑符号等。
• 状态空间方法（Method on State Space)

使用状态空间法解题：1.给出状态描述，特别是初始状态，目标状态，2.给定操作符集合，以及操作符的作业，3.通过使用不同操作符使得从初始状态转移到目标状态

状态空间例题：猴子摘香蕉，传教士过河
（注：不打算作为重点去看）

问题归约法

实质：将原始问题分解一些子问题，通过求解这些子问题可以最终求解原始问题。将得到的子问题不断分解直至得到平凡的本原问题。通过平凡的本原问题的解逆推最终得到原始问题的解。

组成部分

1. 一个初始问题描述；
2. 一套把问题变换为子问题的操作符；
3. 一套本原问题描述。

问题归约的例题：梵塔难题，不定积分的求解、

（注：不打算作为重点去看）

谓词逻辑法(重点 但是不单独考察)

基础概念

• 逻辑主要研究推理过程，而推理过程必须依靠命题来表达。
  命题是陈述客观外界发生事情的陈述句。  命题是或为真或为假的陈述句。学会如何判断一个句子是否为命题
• 命题抽象：取值为0或1的p等符号。
  若p取值1，则表示p为真命题；
  若p取值0，则表示p为假命题
• 复杂命题：由连结词和命题连接而成的更加复杂命题
  复合命题的真假完全由构成它的简单命题的真假所决定。

 命题连接词(五种) 概念性问题，记住即可，没必要浪费时间  

1. 否定  ¬P
2. 合取  p∧q
3. 析取  p∨q
   “相容或”：可以同时发生  ：可表示为p∨q
   “相异或”：不可以同时发生，当且选择其一  ： 可表示为 (p∧ ¬q) ∨ (¬p∧q)
4. 蕴含  p → q     如果p, 则q
5. 等价  p↔q    “p当且 仅当q

命题符号化(第一步 建议多加练习，)直接一步到位，直接看谓词逻辑符号化

照例先给出一些概念：
谓词逻辑法采用谓词合式公式和一阶谓词演算把要解决的问题变为一个有待证明的问题,然后采用消解原理和消解反演来证明一个新语句是从已知的正确语句导出的,从而证明新语句也是正确的.(注：看不懂没关系，有些概念在后边才会给出证明  )

谓词：用于刻画个体的性质、状态和个体之间关系的语言成分。
举例：张三是研究生，李四是研究生
在这个问题中，研究生就是张三和李四共同的属性。使用符号P(x)表示 x是研究生，则上述句子的符号化为 P(张三) ∨ P(李四)

谓词逻辑的语法元素表示如下

• 个体符号或常量:A、B、张三、李四等等，通常是对象的名称。
• 变量符号：习惯上用小写字母表示，如x、y、z等。
• 函数符号：习惯上用小写英文字母或小写英文字母串表 示，如plus、f、g。
• 谓词符号：习惯上用大写英文字母或（首字母）大写英文字母串表示。
• 连接词：否定  合取 析取 蕴含 
  • (说明：暂时不知道函数符号 和 谓词符号之间 怎样区分)
• 量词
  全称量词：若一个原子公式 P(x)，对于所有可能变量x都具有T 值,则用(∀x)P(x)表示
  举例：所有学生都穿彩色制服   (∀x)[Student(x)=>Uniform (x, Color)]
  存在量词：若一个原子公式P(x), 至少有一个变元x可使 P(x) 为T值, 则用(∃x)P(x)表示 
  举例：1号房间内有个物体  (∃x)INROOM(x,r1)

谓词逻辑法表示句子：

1. 刘欢比他父亲有名。
2. 高扬是计算机系的学生，但他不喜欢编程。
3. 人人爱劳动。

第一步：定义如下谓词：

Famous(x,y):x比y有名。 Computer(x): x是计算机系的学生 Like(x,y): x喜欢y Love(x,y): x爱y Man(x): x

第二步：用谓词公式表示

1. Famous(刘欢，刘欢的父亲)
2. Computer(高杨) ∧ ~like(高杨，编程)
3. (∀x)[Man(x)=>Love(x, labour)]

 合式公式：由原子谓词公式经过有限次的连接运算和量词拼接起来的公式

定义类似于初等函数 定义：由 基本初等函数经过有限次四则运算得到的函数

注： 合式公式的性质并不需要全部记，需要记得公式会在后边给出

注意点：

1. 量词否定
   ~ (∃x)P(x)等价于(∀x)[~P(x)]     ~(∀x)P(x)等价于(∃x)[~P(x)]
2. 量词分配
   (∀x)[P(x)∧Q(x)]等价于(∀x)P(x)∧(∀x)Q(x)
3. 量词辖域
   量词的辖域是邻接量词之后的最小子公式， 故除非辖域是个原子公式，否则应在该子公式的两端有括号
   注：找辖域的方法：1.看有无括号 2.紧跟的原子公式
   举例：(∀x)P(x)→Q(x)       ∀x的辖域是P(x)
             (∃x ) [P(x, y)→Q(x，y)] ∨ P(y, z)     ∃x的辖域是P(x，y)→Q(x，y)

利用谓词公式进行知识表示的步骤如下：  (概念 配合例题进行理解)

1. 定义谓词及个体,确定其含义
2. 根据要表达的事物或概念,为每个谓词中的变元赋值;
3. 根据表达的知识的含义,用适当的连接符号将各个谓词连接起来,形成谓词公式

例题：（在练习中去体验每一步应该做什么）

1. 如果张三比李四大，那么李四比张三小
   定义如下谓词：Old(x,y) x比y大    Young(x,y)  x比y小
   用谓词公式表示：Old(张三，李四)=>Young(李四, 张三)
2. 若一个人是老实人，他就不会说谎
   Honest(x)  x是老实的    Man(x）x是人      Lie(x) x撒谎
   Honest(Man(x)) => ~Lie(x)
3. 并不是所有的学生选修了历史和生物
   Student(x) x是学生   learn(x,y) x选修了y
   ~(∀x)[Student(x) => ( learn(x,历史) ∨learn(x,生物)）
4. 所有选修人工智能课程的学生都喜欢玩游戏。
   Student(x) x是学生    learn(x,y) x选修了y    Like(x,y) x喜欢y
   (∀x)[Student(x) ∧  learn(x，AI） => Like（x,games）
5. 历史考试中有学生不及格。
   Fail(x,y) x没有通过y    Student(x)   x是学生
   (∃x)   Student(x) ∧  Fail(x，历史考试)
6. 星期六，所有的学生或者去了舞会，或者去工作， 但是没有两者都去的。
    Student(x)   x是学生     Party(x) x参加舞会   Work(x) x参加工作
     (∀x) Student(x) => ((Party(x) ∧ ~Work(x)) ∨ ((~Party(x) ∧ Work(x)))

置换：在该表达式中用置换项置换变量.
{ti/xi}  用 t1(常量、 变量、函数) 去置换表达式中的 xi(变量)

举例：表达式：P[x,f(y),B]     置换：s2={A/y}  结果：P[x,f(y),B]s2=P[x,f(A),B]
                                                        s1={z/x,w/y}    结果：P[x,f(y),B]s1 = P[z,f(w),B]

合一：寻找项对变量的置换，以使两表达式一致。(对象：两个表达式   操作：做同一个置换 结果：若置换结果相同，则这个置换叫做一个合一)
举例：表达式1{P[x,f(y),B]，          置换：s={A/x,B/y}             结果：P[A,f(B),B]   则这个置换叫做这两个表达式的一个合一
           表达式2P[x,f(B),B]}                                                                 P[A,f(B),B]    
最一般合一：通过置换最少的变量以使表达式一致

语义网络法

语义网络是知识的一种结构化图解表示，它由节点和弧线组成。
      节点用于表示实体、概念和情况等，节点之间的
       弧线用于表示节点间的关系。
在注意一点：语义网络从本质上说只能表示两元关系，题目中的多元关系需要拆分成两元关系

直接看题(不用管那么多)

要表达北京大学(BEIJING University,简称BU) 和清华大学(TSINGHUA University,简称TU)两校篮球队在北大进行的一场比赛的比分是85比89。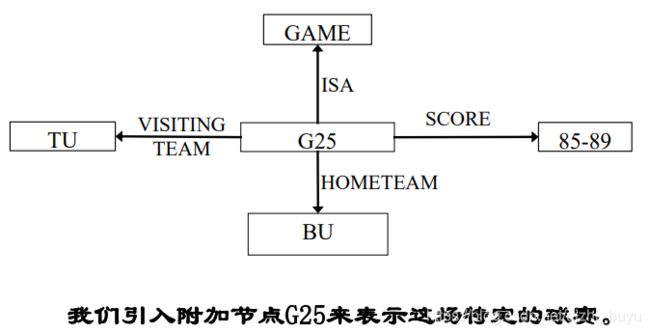

框架

框架是一种结构化表示法，通常采用语义网络中的节点-槽-值表示结构。(框架跟语义网络并没有本质区分)

框架表示：

 <框架名>
              <槽名1>:<槽值1>
             .............
             <槽名n>:<槽值n>

剧本：框架的一种特殊形式。

第三章：搜索技术

基于状态空间法的搜索技术

1. 图搜索策略
2. 盲目搜索
3. 启发式搜索

基于问题归约的搜索技术

1. 与或树搜索
2. 机器博弈

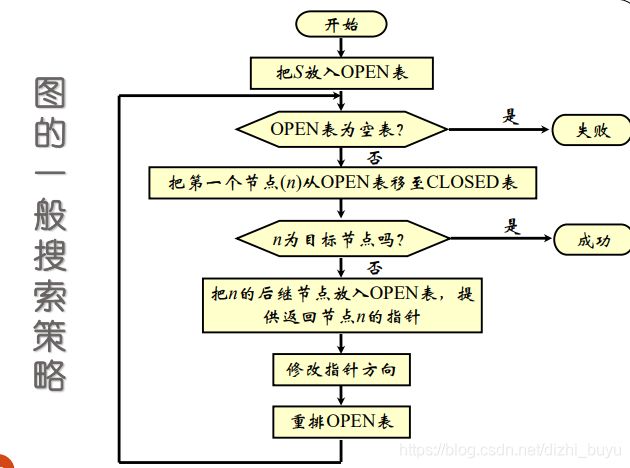
图搜索策略

不知道这块该怎么整理，感觉学的比较乱

这是一个通用的搜索过程,后面讨论的状态空间各种搜索策略都是其特例.各种搜索策略的主要区别就是对OPEN表中节点排序准则不同

盲目搜索

1. 宽度优先搜搜
2. 广度优先搜索
3. 等代价搜索

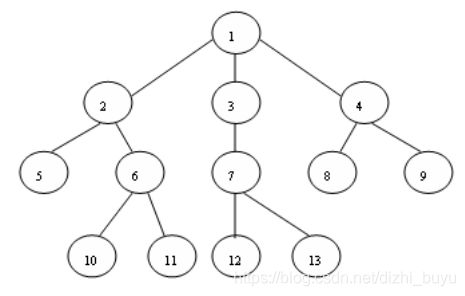
补充题： 列出图中树的节点访问序列以满足下面的两个搜索策略 ,并写出其搜索过程中的 open 和closed表（在所有情况中都选择最左分枝优先访问 , 设节点12为目标节点）：
（ 1）深度优先搜索； （ 2）宽度优先搜索。

   解答：
深度优先访问序列：1,2,5,6,10,11,3,7,12,13,4,8,9
深度优先open表和closed表存储内容
 

open表	closed表
1
2,3,4	1
5,6,3,4	1,2
6,3,4	1,2,5
10,11,3,4	1,2,,5,6
11,3,4	1,2,5,6,10
3,4	1,2,5,6,10,11
7,4	1,2,5,6,10,11,3
12,13,4	1,2,5,6,10,11,3,7
13,4	1,2,5,6,10,11,3,7,12

closed表中找到目标节点12，搜索结束

宽度优先访问序列：1,2,3,4,5,6,7,8,9,10,11,12
宽度优先open表和closed表存储内容

open表	closed表
1
2,3,4	1
3,4,5,6	1,2
4,5,6,7	1,2,3
5,6,7,8,9	1,2,3,4
6,7,8,9	1,2,3,4,5
7,8,9,10,11	1,2,3,4,5,6
8,9,10,11,12,13	1,2,3,4,5,6,7
10,11,12,13	1,2,3,4,5,6,7,8,9
12,13	1,2,3,4,5,6,7,8,9,10,11
13	1,2,3,4,5,6,7,8,9,10,11,12

closed表中找到目标节点12，搜索结束

启发式搜索

特点：重排OPEN表,选择最有希望的节点加以扩展
种类：有序搜索,A*算法
定义估价函数：估算节点 希望程度的量度

有序搜索：选择OPEN表上具有最小f值的节点作为下一个要扩展的节点

A*算法

估价函数：f(n)=g(n)+h(n)  (好家伙，真的看不懂想说啥，还是看题吧)

做题中 需要明确g(n)和h(n)的如何计算，选择其和最小的进行扩展

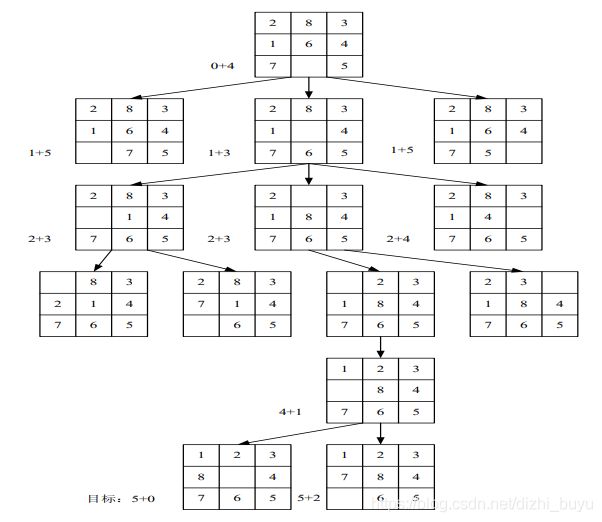
对于如图所示的八数码问题，给出满足A *算法的启发函数，并给出相应的搜索图。

解答：
启发函数的选取如下：g(n)表示节点n在搜索树中的深度，h(n)=ω(n)表示节点n中不在目标状态中相应位置的数码个数，
f(n)= ω(n)+g(n),可以得到如图所示搜索过程。

 

第四章：逻辑推理技术

消解原理

基本概念：

1. 文字：一个原子公式和原子公式的否定都叫做文字  P(x)， ¬P(x,f(x))，
2. 子句：由文字的析取组成的公式    P(x)∨Q(x)  ....  ¬P(x,f(x))∨Q(x,g(x))
3. 子句集：由子句构成的集合。  {P(x)∨Q(x) , ~P(x，f(x)∨Q(x,g(x)) }
4. 合取范式：C1 ∧C2 ∧C3… ∧Cn  由合取连接形成的公式   
5. 消解 

子句集的求取，分为九步：

1. 消去蕴涵符号    只应用∨和～符号，以～A∨B替换A→B
2. 减少否定符号的辖域，每个否定符号～最多只用到一个谓词符号上，并反复应用狄·摩根定律
   以～A∨～B代替～(A∧B）
   以～A∧～B代替～(A∨B)
   以(∃x){～A}代替～(∀x)A
   以(∀x){～A}代替～(∃x)A
   以A代替～(～A)
3. 对变量标准化  两个变量的辖域不重复，若重复，就换变量
4. 消去存在量词  分两种情况
   如果要消去的存在量词在某些全称量词的辖域内，用Skolem函数替换    

   (∀y)[(∃x)P(x,y)    所存在的x可能依赖于y值   所以令 x = g(y)    (∀y)P(g(y),y)
   消去的存在量词不在任何一个全称量词的辖域内   用常量替换

5. 化为前束形

6. 把母式化为合取式， 谓词公式和(或)谓词的否定的析取的有限集组成的合取
   常用公式  A∨{B∧C} 化为 {A∨B}∧{A∨C}  A∨{B∨C} 化为 {A∨B∨C}

7. 消去全称量词

8. 消去连词符号 ∧

9. 更换变量名称

举例：  (∀x) (∃y) {P(x,y) ∨ [Q(x,y) → R(x,y)]}
第一步：消蕴含    (∀x) (∃y) {P(x,y) ∨ [  ~ Q(x,y)  ∨ R(x,y)] }
第二步：减少否定的辖域    (∀x) (∃y) {P(x,y) ∨ [  ~ Q(x,y)  ∨ R(x,y)] }
第三步：变量标准化   (∀x) (∃y) {P(x,y) ∨ [  ~ Q(x,y)  ∨ R(x,y)] }
第四步：消去存在量词   全称量词x 的辖域  (∃y) {P(x,y) ∨ [  ~ Q(x,y)  ∨ R(x,y)] }   存在量词y的辖域  {P(x,y) ∨ [  ~ Q(x,y)  ∨ R(x,y)] }
           所以采用 Skolem函数  令  y = g(x)   (∀x)  {P(x,g(x)) ∨ [  ~ Q(x,g(x))  ∨ R(x,g(x))] }
第五步 ：化为前束形   (∀x)  {P(x,g(x)) ∨ [  ~ Q(x,g(x))  ∨ R(x,g(x))] }
第六步 ：母式华为合取范式  {P(x,g(x)) ∨  ~ Q(x,g(x))  ∨ R(x,g(x)）}
第七步：消去全称量词   {P(x,g(x)) ∨  ~ Q(x,g(x))  ∨ R(x,g(x)）}
第八部 ：消去合取符号  {P(x,g(x)) ∨  ~ Q(x,g(x))  ∨ R(x,g(x)）}
第九步：更换变量名称 {P(x,g(x)) ∨  ~ Q(x,g(x))  ∨ R(x,g(x)）}

注：说一下子句集化简要求(掌握基本的化简要求即可)，练习题的谓词公式给的比较复杂，可以作为检验内容，实际问题中不会那么多符号的。

消解反演：设F1、 … 、Fn、G为公式，G为F1、 … 、Fn的逻辑推论，当且仅当公式（（F1∧…∧Fn）→G）①是有效的.(如何 F 那么G ，通过合式公式性质A→B  等价于～A∨B

可以得到)。~(F1∧…∧Fn ) ∨ G ②。然后取否定 (F1∧…∧Fn ) ∧ ~G  ③  证明③式矛盾(不成立)，来说明 ②式成立，继而①式成立

消解的定义：令L1,L2为两任意原子公式： L1和L2具有相同的谓词符号，但一般具有不同的变量，已知两个子句 L1 ∨ α和～ L2 ∨ β，如果L1和L2具有最一般合 一σ,那么通过消解可以从两个父辈子句推导出一个新子句（α∨β）σ 。 这个新子句叫做消解式。
(注：消解步骤 1.找相同的谓词公式  存在公式及其否定 2.找两者之间的最一般合 一σ   3.剩余部分之间做析取，然后做置换σ   必须会）

重言式：公式及公式的否定两者取析取

举例 1.：(要求 ：熟悉消解反演证明的步骤)
前提：(P →Q) ∧~Q    结论： ~P    
证明步骤：一 .对前提(条件)   和   结论的否定  化成子句集形式 
( ~P ∨ Q）∧ ~Q   ，然后 { ~P ∨ Q， ~Q }            在加上结论的否定  得到 { ~P ∨ Q， ~Q，P}  不妨设置编号为 1,2,3
                  二  使用消解原则进行归结
                       1,2归结得到 ~P  命名为4     3,4归结得到 NIL    所以原命题成立

举例2：练习题 
已知：F：(∀x)[(∃y) ( A(x,y) ∧ B(y)) → (∃y) ( C(y) ∧ D(x,y))]
           G:  ~(∃x) C(x) → (∀x)(∀y) (A(x,y) → ~ B(y))
求证：G是F的逻辑结论。
解：首先：将 F 和  ~G 化后子句集形式   (注：我觉得按照G的形式 先化简，后带入~ 能简单点)
F：(∀x)[(∃y) ( A(x,y) ∧ B(y)) → (∃y) ( C(y) ∧ D(x,y))]
      (∀x)[ ~ [(∃y) ( A(x,y) ∧ B(y))] ∨ (∃y) ( C(y) ∧ D(x,y))]
      (∀x)[ (∀y) ( ~ A(x,y) ∨ ~B(y)) ∨ (∃y) ( C(y) ∧ D(x,y))]
      (∀x)[ (∀y) ( ~ A(x,y) ∨ ~B(y)) ∨ (∃w) ( C(w) ∧ D(x,w))]
全称量词 x 的辖域 [   (∀y) ( ~ A(x,y) ∨ ~B(y)) ∨ (∃w) ( C(w) ∧ D(x,w))]    全称量词 y:( ~ A(x,y) ∨ ~B(y))   存在量词w：( C(w) ∧ D(x,w))
令 w = f(x)    (∀x)[ (∀y) ( ~ A(x,y) ∨ ~B(y)) ∨  ( C(f(x)) ∧ D(x,f(x)))]
     (∀x) (∀y)[ ( ~ A(x,y) ∨ ~B(y)) ∨  ( C(f(x)) ∧ D(x,f(x)))]
     ( ~ A(x,y) ∨ ~B(y)  ∨  C(f(x))   ) ∧  ( ~ A(x,y) ∨ ~B(y) ∧ D(x,f(x)))
     { ~ A(x,y) ∨ ~B(y)  ∨  C(f(x)),  ~ A(x,y) ∨ ~B(y) ∧ D(x,f(x))}      给定编号：1,2

G:~(∃x) C(x) → (∀x)(∀y) (A(x,y) → ~ B(y)) 
    ~[ ~(∃x) C(x) ] ∨ (∀x)(∀y) (A(x,y) → ~ B(y))    在来一次  ~[ ~(∃x) C(x) ] ∨ { ~ (∀x)(∀y) (A(x,y)  ∨ ~ B(y) }
    (∃x) C(x) ∨ { (∃x)(∃y)~ (A(x,y) ∨ ~ B(y) }
    (∃u) C(u) ∨ { (∃x)(∃y)~ (A(x,y) ∨ ~ B(y) }   
    令 u= z , x = a , y = b   C(a) ∨ { ~ (A(a,b) ∨ ~ B(b) }
     C(a) ∨ ~ (A(a,b) ∨ ~ B(b) 
所以 ~G: ~ [C(a) ∨ ~ (A(a,b) ∨ ~ B(b)  ]  = ~C(a) ∧  (A(a,b) ∧ B(b) 
~G:{ ~C(a) , A(a,b) , B(b) }   给定编号：3,4,5

然后 使用消解原则进行归结   (注：归结顺序可以不一样，)
~B(b)  ∨  C(f(x)）      14归结   a/x b/y    得到   6
~B(b)       3,6归结   a/f(x)     得到  7
NIL           5,7归结    得到8

所以G是F的逻辑结论

举例3：(注：实际问题求解）
某公司招聘工作人员，A、B、C三人应试，经面试 后公司表示如下想法：
（1）三人中至少录取一人。（2）如果录取A而不录取B，则一定录取C。 （3）如果录取B，则一定录取C。
  求证：公司一定录取C。

解：首先 向所给出的条件和知识用谓词公式表示
定义:P(x) 表示 公司录取 x 
(1)  P(A)∨ P(B) ∨P(C)  （2） [ P(A)∧ ~P(B) ]  → P(C)   （3） P(B)  → P(C)    结论：P(C)

将谓词公式表示成子句集形式，并给出编号  (注：可以不用分开写，写出谓词公式后面紧跟写出子句集)
{P(A)∨ P(B) ∨P(C)} 1   { ~ P(A) ∨P(B) ∨ P(C)}   2     { ~P(B) ∨ P(C) }   3     {~P(C)}  4

归结，得出结论
P(B) ∨ P(C)    1,2归结   得到   5
P(C)                3,5归结   得到   6
NIL                  4,6归结   得到   7 
所以：公司一定录取C

 

 

 

 

 

  

.