随机游走问题的神奇应用(三)
二维变概率问题的Matlab GUI设计
-
- 一.方程的基本形式
- 二.基本框架的搭建
- 三.关键函数
一.方程的基本形式
a ( P ) ∂ 2 u ∂ x 2 + b ( P ) ∂ 2 u ∂ y 2 + c ( P ) ∂ u ∂ x + d ( P ) ∂ u ∂ y + e ( P ) u ( P ) = q ( P ) , p ∈ D u ( Q ) = f ( Q ) , Q ∈ Γ = ∂ D a(P)\frac{\partial ^2u}{\partial x^2}+b(P)\frac{\partial ^2u}{\partial y^2}+c(P)\frac{\partial u}{\partial x}+d(P)\frac{\partial u}{\partial y}+e(P)u(P) = q(P),p\in D\\ u(Q) = f(Q),Q\in\Gamma = \partial D a(P)∂x2∂2u+b(P)∂y2∂2u+c(P)∂x∂u+d(P)∂y∂u+e(P)u(P)=q(P),p∈Du(Q)=f(Q),Q∈Γ=∂D
若 a ( P ) , b ( P ) > 0 , e ( P ) ≤ 0 a(P),b(P)>0,e(P)\leq 0 a(P),b(P)>0,e(P)≤0求 u ( P ) , p ∈ D u(P),p\in D u(P),p∈D的数值解。
解法参考
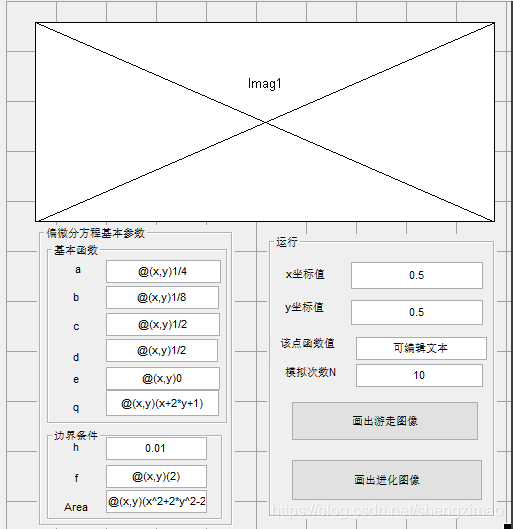
二.基本框架的搭建
三.关键函数
随机游走函数:
function [uFinal,zeta,FirstPx,FirstPy,u] = possionRandomChangeGUI(xPoint,yPoint,a,b,c ,d ,e,q,f,Constrain,h,N)
%UNTITLED 求a = 1/4;b = 1/8;c = 1/2;d = 1/2;e = 0;q = x+2y+1 在u(L) = 2边界条件
% [xPoint,yPoint]表示该点坐标,h仿真步长,N仿真次数
u = zeros(1,N);
W = @(x,y)(1-h^2*e(x,y)/(2*(a(x,y)+b(x,y))))^(-1);
Z = @(x,y)(q(x,y)/(a(x,y)+b(x,y)));
for i = 1:N
sumV = 0;
xValue = xPoint;
yValue = yPoint;
P = [xValue ,yValue];
Ws = 1;
%以下是游走过程
while(1)
if Constrain(xValue,yValue)>0
P = [P;xValue,yValue];
break;
end
A = (2*a(xValue,yValue)+h*c(xValue,yValue))/(4*(a(xValue,yValue)+b(xValue,yValue)));
B = (2*a(xValue,yValue)-h*c(xValue,yValue))/(4*(a(xValue,yValue)+b(xValue,yValue)));
C = (2*b(xValue,yValue)+h*d(xValue,yValue))/(4*(a(xValue,yValue)+b(xValue,yValue)));
D = (2*b(xValue,yValue)-h*d(xValue,yValue))/(4*(a(xValue,yValue)+b(xValue,yValue)));
randNumber = randsrc(1,1,[[0 1 2 3];[A C B D]]);
switch (randNumber)
case 0
xValue = xValue + h;
yValue = yValue;
case 1
xValue = xValue ;
yValue = yValue + h;
case 2
xValue = xValue - h ;
yValue = yValue ;
case 3
xValue = xValue;
yValue = yValue - h;
end
P = [P;xValue,yValue];
end
%以下是画图过程
if i == 1
FirstPx = P(:,1);
FirstPy = P(:,2);
end
%以下是计算过程
[m,n] = size(P);
for j = 1:m-1
Ws = Ws*W(P(j,1),P(j,2));
sumV = sumV + Ws*Z(P(j,1),P(j,2));
end
zeta(i) = -h^2/2*sumV + Ws*f(P(m,1),P(m,2));
u(i) = sum(zeta(1:i))/i;
end
uFinal = u(N);
% xlabel('次数');
% ylabel('进化曲线');
% title('收敛过程');
end
两个按键的回调函数:
% --- Executes on button press in walk.
function walk_Callback(hObject, eventdata, handles)
% hObject handle to walk (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
af = str2func(get(handles.a,'String'));
bf = str2func(get(handles.b,'String'));
cf = str2func(get(handles.c,'String'));
df = str2func(get(handles.d,'String'));
ef = str2func(get(handles.e,'String'));
qf = str2func(get(handles.q,'String'));
hn = str2num(get(handles.h,'String'));
ff = str2func(get(handles.f,'String'));
Areaf = str2func(get(handles.Area,'String'));
xLP = str2num(get(handles.xL,'String'));
yLP = str2num(get(handles.yL,'String'));
N = str2num(get(handles.N,'String'));
[uFinal,zeta,FirstPx,FirstPy,u] = possionRandomChangeGUI(xLP,yLP,af,bf,cf ,df ,ef,qf,ff,Areaf,hn,N);
set(handles.uxy,'String',num2str(uFinal));
axes(handles.Imag1);
plot(FirstPx,FirstPy,'b.-');
xlabel('x');
ylabel('y');
title('第一次的轨迹');
% --- Executes on button press in breakUp.
function breakUp_Callback(hObject, eventdata, handles)
% hObject handle to breakUp (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
af = str2func(get(handles.a,'String'));
bf = str2func(get(handles.b,'String'));
cf = str2func(get(handles.c,'String'));
df = str2func(get(handles.d,'String'));
ef = str2func(get(handles.e,'String'));
qf = str2func(get(handles.q,'String'));
hn = str2num(get(handles.h,'String'));
ff = str2func(get(handles.f,'String'));
Areaf = str2func(get(handles.Area,'String'));
xLP = str2num(get(handles.xL,'String'));
yLP = str2num(get(handles.yL,'String'));
N = str2num(get(handles.N,'String'));
[uFinal,zeta,FirstPx,FirstPy,u] = possionRandomChangeGUI(xLP,yLP,af,bf,cf ,df ,ef,qf,ff,Areaf,hn,N);
axes(handles.Imag1);
plot(1:N,u,'r-');
xlabel('次数');
ylabel('进化曲线');
title('收敛过程');
set(handles.uxy,'String',num2str(uFinal));