计算WPL·哈夫曼树构建及带权路径长计算

题目信息

Huffman编码是通信系统中常用的一种不等长编码，它的特点是：能够使编码之后的电文长度最短。

输入

第一行为要编码的符号数量n
第二行～第n+1行为每个符号出现的频率

输出

对应哈夫曼树的带权路径长度WPL

测试样例

测试样例1

5
7
5
2
4
9

WPL=60

测试样例2

5
2
4
2
3
3

WPL=32

解答

#include

using namespace std;

struct BTreeNode
{
     
    int data;
    BTreeNode *Left;
    BTreeNode *Right;
};

//2、根据数组 a 中 n 个权值建立一棵哈夫曼树，返回树根指针
BTreeNode *CreateHuffman(int *a, int n)
{
     
    BTreeNode *b[n];
    for (int i = 0; i < n; i++) //初始化b指针数组，使每个指针元素指向a数组中对应的元素结点
    {
     
        b[i] = new BTreeNode;
        b[i]->data = a[i];
        b[i]->Left = NULL;
        b[i]->Right = NULL;
    }
    BTreeNode *q = new BTreeNode;
    for (int i = 1; i < n; i++)//进行 n-1 次循环建立哈夫曼树
    {
     //k1表示森林中具有最小权值的树根结点的下标，k2为次最小的下标
        int k1 = -1, k2;
        for (int j = 0; j < n; j++)
        {
     //让k1初始指向森林中第一棵树，k2指向第二棵
            if (b[j] != NULL && k1 == -1)
            {
     
                k1 = j;
                continue;
            }
            if (b[j] != NULL)
            {
     
                k2 = j;
                break;
            }
        }
        for (int j = k2; j < n; j++)//从当前森林中求出最小权值树和次最小
        {
     //此时k1为最小，k2为次最小
            if (b[j] != NULL)
            {
     
                if (b[j]->data < b[k1]->data)
                {
     
                    k2 = k1;
                    k1 = j;
                }
                else if (b[j]->data < b[k2]->data)
                {
     
                    k2 = j;
                }
            }
        }
        //由最小权值树和次最小权值树建立一棵新树，q指向树根结点
        q = new BTreeNode;
        q->data = b[k1]->data + b[k2]->data;
        q->Left = b[k1];
        q->Right = b[k2];
        b[k1] = q;//将指向新树的指针赋给b指针数组中k1位置
        b[k2] = NULL;//k2位置为空
    }
    return q; //返回整个哈夫曼树的树根指针
}

//3、求哈夫曼树的带权路径长度
int WeightPathLength(BTreeNode *Node, int len)
{
     //len初始为0
    if (Node == NULL)
    {
      //空树返回0
        return 0;
    }
    else
    {
     
        if (Node->Left == NULL && Node->Right == NULL)
        {
     //访问到叶子结点
            return Node->data * len;
        }
        else
        {
     //访问到非叶子结点，进行递归调用，返回左右子树的带权路径长度之和，len递增
            return WeightPathLength(Node->Left, len + 1) + WeightPathLength(Node->Right, len + 1);
        }
    }
}


int main()
{
     
    //freopen("/Users/zhj/Downloads/test.txt", "r", stdin);
    int n;
    cin >> n;
    int a[100];
    for (int i = 0; i < n; i++)
    {
     
        cin >> a[i];
    }
    BTreeNode *Root = CreateHuffman(a, n);
    cout << "WPL=" << WeightPathLength(Root, 0) << endl;
}

想法

假设我们给定a,b,c,d,e,f的权值分别为9,12,6,3,5,15
1、首先，我们将权值从小到大排序即3,5,6,9,12,15。

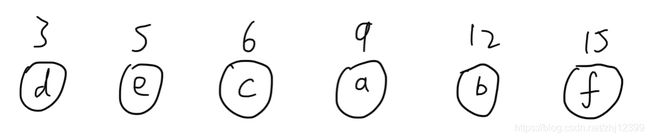
2、选取最小的两个权值3和5构建子树。3 + 5 = 8作为3,5的父节点（我们规定要满足左子节点小于右子节点）。

3、顺序提取6作为左子节点，8作为右子节点。将6 + 8 = 14作为其父节点。

4、我们发现14大于接下来的9,12。故将9,12作为子节点，9 + 12 = 21为其父节点构建一个子树。提取元素15，作为右节点上一步构建的14作为左节点，将14 + 15 = 29作为他们的父节点构建另一个子树。

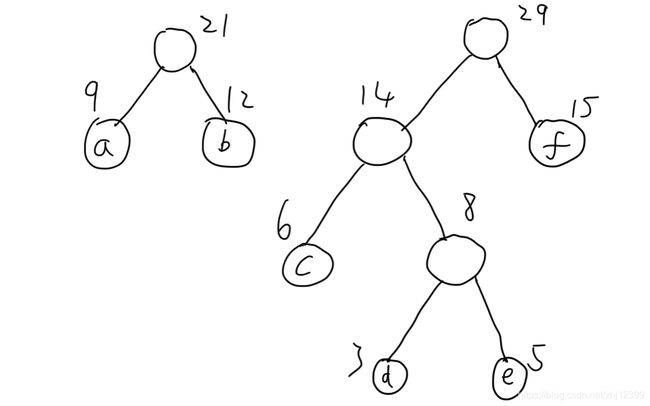
5、最后将上述两个子树的父节点21,29分别作为左节点和右节点。将21 + 29 = 50作为他们的父节点。这样就构造出了一个哈夫曼树。

6、接下来进行带权路径长的计算：
a，b，f（权值9,12,15）三个元素距父节点的距离都为2
c（权值6）元素距父节点的距离为3
d，e（权值3,5）元素距父节点的距离为4
故这棵哈夫曼树的WPL为：WPL =（9 + 12 + 15）*2 + 6 * 3 + （3 + 5）* 4 = 122
7、哈夫曼编码
从哈夫曼树根节点开始，对左子树分配代码“0”，对右子树分配“1”，一直到达叶子节点。然后，将从树根沿着每条路径到达叶子节点的代码排列起来，便得到每个叶子节点的哈夫曼编码，如下图。

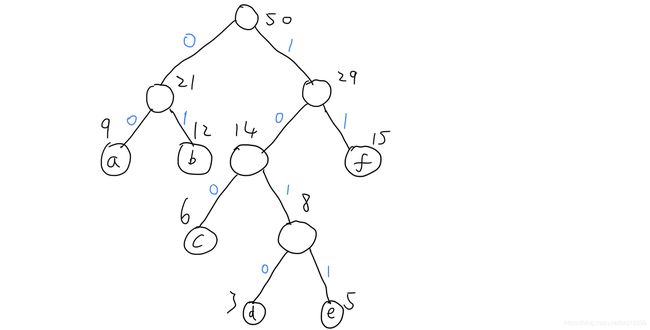
从图中可以看出：
a 的编码为：00
b 的编码为：01
c 的编码为：100
d 的编码为：1010
e 的编码为：1011
f 的编码为：11
8、下面用详细的程序展示哈夫曼树的操作

#include

using namespace std;

struct BTreeNode
{
     
    int data;
    BTreeNode *Left;
    BTreeNode *Right;
};

//1、输出二叉树，可在前序遍历的基础上修改。采用广义表格式
void PrintBTree(BTreeNode *Node)
{
     
    if (Node != NULL)
    {
     
        cout << Node->data; //输出根结点的值
        if (Node->Left != NULL || Node->Right != NULL)
        {
     
            cout << "(";
            PrintBTree(Node->Left); //输出左子树
            if (Node->Right != NULL)
            {
     
                cout << ",";
            }
            PrintBTree(Node->Right); //输出右子树
            cout << ")";
        }
    }
}

//2、根据数组 a 中 n 个权值建立一棵哈夫曼树，返回树根指针
BTreeNode *CreateHuffman(int *a, int n)
{
     
    BTreeNode *b[n];
    for (int i = 0; i < n; i++) //初始化b指针数组，使每个指针元素指向a数组中对应的元素结点
    {
     
        b[i] = new BTreeNode;
        b[i]->data = a[i];
        b[i]->Left = NULL;
        b[i]->Right = NULL;
    }
    BTreeNode *q = new BTreeNode;
    for (int i = 1; i < n; i++)//进行 n-1 次循环建立哈夫曼树
    {
     //k1表示森林中具有最小权值的树根结点的下标，k2为次最小的下标
        int k1 = -1, k2;
        for (int j = 0; j < n; j++)
        {
     //让k1初始指向森林中第一棵树，k2指向第二棵
            if (b[j] != NULL && k1 == -1)
            {
     
                k1 = j;
                continue;
            }
            if (b[j] != NULL)
            {
     
                k2 = j;
                break;
            }
        }
        for (int j = k2; j < n; j++)//从当前森林中求出最小权值树和次最小
        {
     //此时k1为最小，k2为次最小
            if (b[j] != NULL)
            {
     
                if (b[j]->data < b[k1]->data)
                {
     
                    k2 = k1;
                    k1 = j;
                }
                else if (b[j]->data < b[k2]->data)
                {
     
                    k2 = j;
                }
            }
        }
        //由最小权值树和次最小权值树建立一棵新树，q指向树根结点
        q = new BTreeNode;
        q->data = b[k1]->data + b[k2]->data;
        q->Left = b[k1];
        q->Right = b[k2];
        b[k1] = q;//将指向新树的指针赋给b指针数组中k1位置
        b[k2] = NULL;//k2位置为空
    }
    return q; //返回整个哈夫曼树的树根指针
}

//3、求哈夫曼树的带权路径长度
int WeightPathLength(BTreeNode *Node, int len)
{
     //len初始为0
    if (Node == NULL)
    {
      //空树返回0
        return 0;
    }
    else
    {
     
        if (Node->Left == NULL && Node->Right == NULL)
        {
     //访问到叶子结点
            return Node->data * len;
        }
        else
        {
     //访问到非叶子结点，进行递归调用，返回左右子树的带权路径长度之和，len递增
            return WeightPathLength(Node->Left, len + 1) + WeightPathLength(Node->Right, len + 1);
        }
    }
}

//4、哈夫曼编码（可以根据哈夫曼树带权路径长度的算法基础上进行修改）
void HuffManCoding(BTreeNode *Node, int len)//len初始值为0
{
     
    static int a[100];//定义数组a，保存每个叶子的编码，数组长度至少是树深度减一
    if (Node != NULL)
    {
     
        if (Node->Left == NULL && Node->Right == NULL)
        {
     //访问到叶子结点时输出其保存在数组a中的0和1序列编码
            cout << "结点权值为" << Node->data << "的编码：";
            for (int i = 0; i < len; i++)
            {
     
                cout << a[i];
            }
            cout << endl;
        }
        else//访问到非叶子结点时分别向左右子树递归调用，并把分支上的0、1编码保存到数组a
        {
        //的对应元素中，向下深入一层时len值增1
            a[len] = 0;
            HuffManCoding(Node->Left, len + 1);
            a[len] = 1;
            HuffManCoding(Node->Right, len + 1);
        }
    }
}

int main()
{
     
    freopen("/Users/zhj/Downloads/test.txt", "r", stdin);
    int n;
    cout << "输入待构造的哈夫曼树中带权叶子结点数n：" << endl;
    cin >> n;
    cout << "输入" << n << "个整数作为权值：" << endl;
    int a[100];
    for (int i = 0; i < n; i++)
    {
     
        cin >> a[i];
    }

    BTreeNode *Root = CreateHuffman(a, n);
    cout << "广义表形式的哈夫曼树：";
    PrintBTree(Root);
    cout << endl << "哈夫曼树的带权路径长度,既WPL值：" << WeightPathLength(Root, 0) << endl;
    cout << "树中每个叶子结点的哈夫曼编码:" << endl;
    HuffManCoding(Root, 0);
}