CS224W笔记-第十六课
第16课——网络的演化
由于项目的关系,提前看一下网络演化这一课。为项目提供一些思路。
网络的演进是一个非常常见的场景,随着时间的变化,一个网络的节点和边都会有增有减,相应的网络结构随之改变。同样的,网络节点和边的特征也会随着时间而改变。不过本节课更关注的是网络结构层面的改变,而非节点或者边的特征的改变。
网络结构改变的情况使用网络可视化的方法可以比较容易地被观察者定性地发现,但是如何定量地研究网络结构的改变?
课程里介绍了对于网络演变研究的三个层次:
- 宏观(Macro)层面:研究整体演进的模型、密集度等;
- 中观(Meso)层面:研究类似Motif、社区层面的演进;
- 微观(Micro)层面:细化到节点和边的特征的演进研究。
宏观层面研究案例
对于这个层面的案例,Jure给出了他之前研究的一个论文,研究的题目是:
- 在不同时间点,网络上的点 n ( t ) n(t) n(t)和边 e ( t ) e(t) e(t)的关系,比如,如果点的数量增加一倍,边的数量会如何变化?
- 网络的直径随时间会如何变化?
- 网络的节点度分布会如何演化?
问题一:点和边关系的演进关系
如果网络里面点在 t t t时刻的数量 n n n如果在 t + 1 t+1 t+1时刻变成 2 n 2n 2n,那么边的数量 e e e是否会变成 2 e 2e 2e,即是否是线性增加的?研究显示,边的数量要比 2 e 2e 2e多很多,但近似符合密集幂分布律(Densification Power Law)。
随着网络节点的增长,网络连接数会增加,且快于节点数量的增加。即节点的平均度会增加。
密集幂分布律: E ( t ) ∝ N ( t ) α E(t) \propto N(t)^{\alpha} E(t)∝N(t)α,或者 l o g ( E ( t ) ) l o g ( N ( t ) ) = c o n s t \displaystyle \dfrac{log(E(t))}{log(N(t))} = const log(N(t))log(E(t))=const
其中, α \alpha α是密集化系数 ( 1 ⩽ α ⩽ 2 ) (1\leqslant \alpha \leqslant 2) (1⩽α⩽2)。
a = 1 a=1 a=1,则网络是线性增长的,和通常的假设判断一样。
a = 2 a=2 a=2,二次方增长,即网络是全连接的。
a a a也有可能会小于1,如果节点之间的连接会逐步消失。
问题二:网络直径的变化
在第二课里我们研究网络直径的时候,结论是网络的直径会大致等同于节点数量 N N N的对数 l o g ( N ) log(N) log(N)。按照这个结果,当网络节点数量变大后,网络的直径应该会继续增长。但是,研究的结果表明网络直径的会随着网络节点数量的增加,而缓慢地缩短。
这里Jure给出了计算网络直径的具体的方法。
- 并不采用最长最短路径的值,而是使用90%分位数值,或是平均值。这是因为一些极端情况会让最长最短路径很不稳定。
- 只计算最大连接组件的直径。
问题二的答案似乎是和问题一的结果相关的,因为边的数量的增加,所以导致网络直径的减少。但是否是真的如此吗?课程给出了一个模拟随机网络的例子,使用了第二课里讲到的E-R随机网络来演示网络大小和直径的关系。
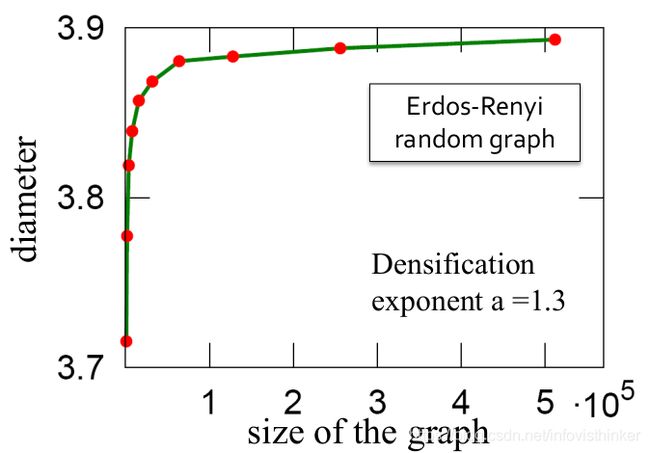
上图里面使用了密集化系数 α = 1.3 \alpha = 1.3 α=1.3,保证模拟的图随着节点的增加,边的数量增加的更快。如果仅仅是图边的增加,图直径应该变短的。但是模拟的结果确是,图变密集时,E-R随机图的直径逐渐增加,尽管增大的速度越来越小。这就说明,图直径的变小还有其他的原因。
课程给出了另外一个解释,即图的度分布的变化导致了图的直径变小。如何验证这个想法捏?课程里给的方法是比对真实图和模拟的具有相同的度分布图的直径。下图给出了论文引用数据集的比较结果。
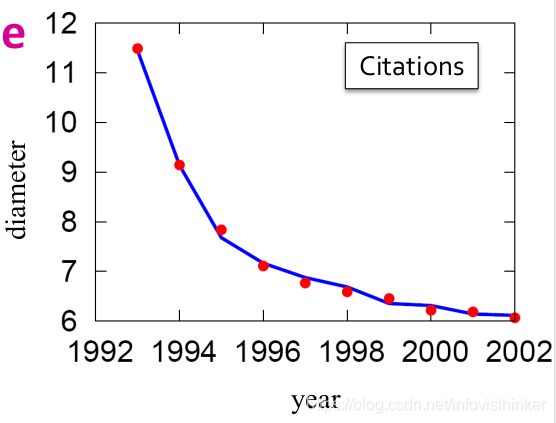
比对的结果给出了图直径变小的原因:密集化 + 度分布变化。
问题三:度分布的演进是如何导致图直径变小的?
对于这个问题,可以有两种假设。
假设1: 图的度分布指数 γ \gamma γ保持不变,即 γ t = γ \gamma_t=\gamma γt=γ。度分布指数是值在进行 l o g − l o g log-log log−log度vs点计数后的直线的斜率的正数值。
在这种情况下,随着点的数量的增加,边也会进一步增加,但是总体的度分布保持不变。表现出来的形式就是 l o g − l o g log-log log−log直线保持斜率不变,只是随着时间向右边移动,并带来更多的具有高度的度的点。同时,如果 γ ∈ [ 1 , 2 ] \gamma \in [1,2] γ∈[1,2],这么图的平均度,即度的期望值是无穷大。这时候图就一直变大,但是直径并不会变小。
假设2: 图的度分布指数 γ \gamma γ会随着图的点的变化而变化,比如当 γ t = 4 n t x − 1 − 1 2 n t x − 1 − 1 \gamma_t = \dfrac{4n_t^{x-1} - 1}{2n_t^{x-1}-1} γt=2ntx−1−14ntx−1−1时, α = x \alpha=x α=x。
这个时候,当节点随着时间越来越大的时候, γ t \gamma_t γt会趋近于2。且图的平均度,即度的期望值是 E [ X ] = γ t − 1 γ t − 2 x m E[X]=\dfrac{\gamma_t - 1}{\gamma_t - 2} x_m E[X]=γt−2γt−1xm。
这个时候,把 γ \gamma γ画出来,它就一步一步地降低。从而让图的直径逐步地变短。
下面就给出了一个图生成模型,用来模拟随着图的扩大及密集化,同时直径也缩小的情况。
森林火灾模型(Forest Fire Model)
森林火灾模型是对于图中新加入节点的连接进行构造的一个模型,比喻成森林大火的传播模式。其基本思想是:
- 设定两个概率:
- p p p:前向传播(着火)的概率
- r r r:反向传播(着火)的概率 - 每次加入一个新的节点 v v v
- 从图中平均概率随机选一个点 w w w作为初始“大使”节点
- 然后基于 p p p和 r r r,按照概率算出 w w w的“入”度 x x x和“出”度 y y y节点的数量。其中, p p p的 r r r对应关系遵照几何分布 P r ( X = k ) = ( 1 − p ) k − 1 p Pr(X=k) = (1-p)^{k-1}p Pr(X=k)=(1−p)k−1p。具体的计算是(这里k=0):
- x = p / ( 1 − p ) x=p/(1-p) x=p/(1−p)
- y = r p / ( 1 − r p ) y=rp/(1-rp) y=rp/(1−rp)
- 根据得出的“入”和“出”度对应的节点和 v v v建立连接;
- 对于新连接的点,采用同样的概率 p p p和 r r r计算新的“入”和“出”度的点数,然后再重复步骤5;
- 重复上述过程,直到没有新的点能和初始的 v v v建立连接。
使用森林火灾模型,模拟图演进的结果显示:随着图节点数量的增加,边的数量会增加的更快,图逐渐密集化;同时图的直径逐步在减少。按照这个模型产出的图,点和边的数量会遵循 l o g − l o g log-log log−log线性关系。
一个有趣的模拟是对于森林火灾模型的参数的修改,会对图演进的结果产生什么影响。见下图:
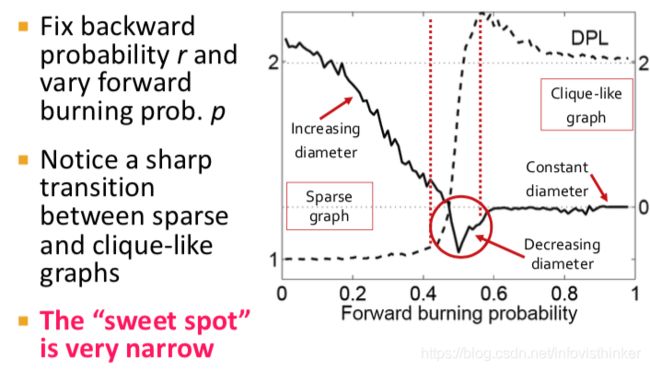
上图中,对于 r r r和 p p p的设定是固定 r r r,然后改变 p p p,从0到1,0表示每次一个新的节点加入,只和图中一个原有的节点相连;而1标识每次新加入的节点都会和图中已经有的节点全连接起来。这是X轴。Y轴有左右两个,数据线也有两条。其中,虚线表示图的密集化指标,实现是图的直径。但是图里的DPL没搞懂是是啥密集化的指标,图的直径的数值也貌似无法和两个Y轴的值对上。不过基本意思是清晰的,即如果前向传播概率小,则生成的图会稀疏,图直径大;如果前向传播概率很大,那么基本上生成的图就是全连接的图,图非常密集,图直径为1。
在这两种情况中间,有一个不大的数值区间 ( 0.4 ∼ 0.6 ) (0.4 \sim 0.6) (0.4∼0.6)。在这个区间里,图的性质随着前向传播概率的增加发生了急剧地变化。从稀疏变密集,图直径从大开始变小。
上面就是关于宏观尺度上观察图演进的3个案例。基本上研究的是整图的一些统计性质随着一些特性的变化如何变化的问题。这个时候,我们研究的图是不同时间周期内的snapshot。如果细化到微观尺度,观察节点级别的问题,就需要预先定义一下时序图。
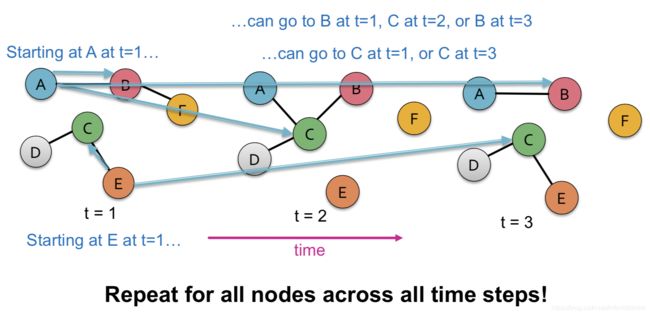
时序图(Temporal Networks)
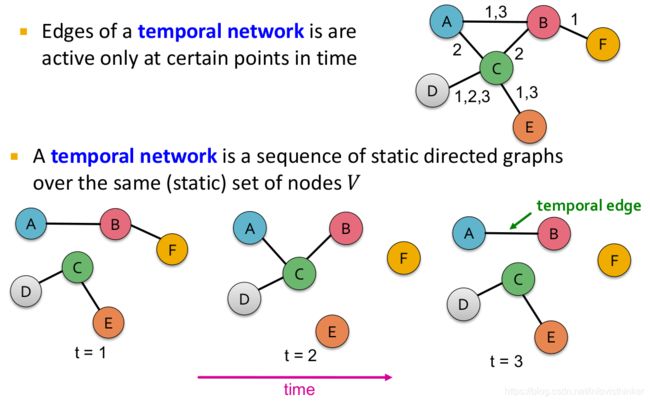
时序图:对于同一批节点,在不同的时刻所形成的一系列静态的有向图。
时序图的一个特殊的定义就是节点始终不变,而边在变化。所以就形成了时序边的概念:
时序边:是按照时间顺序排列的边 ( e i = ( u , v ) , t i ) (e_i=(u, v), t_i) (ei=(u,v),ti)。其中边 ( u , v ) ∈ V (u, v) \in V (u,v)∈V,而 t i t_i ti记录了一条边存在的时间戳。
按照这个定义,课程里给出了一个样例,见下图。在时刻 t = 1 , t = 2 , t = 3 t=1, t=2, t=3 t=1,t=2,t=3不同时间,图的结构是不一样的。
课程里给出了一些时序图的例子,比如通信网络、人际关系、空间共现等。但是这些例子里,我们如果需要满足同一套节点这个限制,就会在数据准备方面带来一些问题和挑战。
微观层面研究案例
基于上面定义的时序图,课程里介绍了一系列的微观层面研究图演进的方法。
主要的研究目标是:当网络增大时,图中的局部特征有什么变化。具体的问题是:
- 如何在时序图里定义“路径”和“游走”?
- 如何在时序图上扩展对中心度的度量(即Pagerank值)?
时序路径:一系列首尾相连的时序边, ( u 1 , u 2 , t 1 ) , ( u 2 , u 3 , t 2 ) , … , ( u i , u i + 1 , t i ) (u_1, u_2, t_1), (u_2, u_3, t_2), \dots, (u_i, u_{i+1}, t_i) (u1,u2,t1),(u2,u3,t2),…,(ui,ui+1,ti)。且 t 1 ≤ t 2 ≤ t 3 , … , ≤ t i t_1\leq t_2 \leq t_3, \dots , \leq t_i t1≤t2≤t3,…,≤ti,同时每个节点都只被访问了一次。
和正常的图里的路径类似,对于时序路径,我们也希望找到两个节点间的最短时序路径。正常的图里面,寻找最短路径的算法是Dijkstra算法,在时序图里也有类似的算法,即TPSP-Dijkstra算法。
算法的细节这里就不再讲了,基本的思想就是在某个时刻去查询两个节点间的最短路径。具体的方法是Dijkstra的方法,只是加入了时序边的限制,即伪代码的第13行所比较的内容。
时序临近度(temporal closeness):获取时序最短路径的目的之一是计算单个节点的时序临近度,即节点在时间范围 [ 0 , t ] [0, t] [0,t]内到所有其他节点的最短路径和的倒数。这个指标可以用来表示节点的中心度的值,具体的计算公式是: C c l o s = 1 ∑ y d ( y , x ∣ t ) C_{clos}=\dfrac{1}{\sum_y d(y, x|t)} Cclos=∑yd(y,x∣t)1,这个值越大临近度越高。
一个学生问了时序临近度的计算复杂度的问题,因为两两节点进行比较需要 N 2 N^2 N2次计算最短时序路径。Jure给出的回答是:在实际计算时,一般用“采样”的方法来降低计算复杂度。
时序PageRank:
研究微观图演进的一个课题是对于Pagerank值的变化的研究。其出发点是对于一个时序图,图中节点在不同时间的入度连接是不同的,在某个时间Pagerank值比较高的节点,时间变化后,可能它的值会发生变化。
这个部分又涉及到了一个新的概念,时序游走:
时序游走是一系列的边 ( u 1 , u 2 , t 1 ) , ( u 2 , u 3 , t 2 ) , . . . . . . , ( u j , u j + 1 , t j ) (u_1, u_2, t_1), (u_2, u_3, t_2), ......, (u_j, u_{j+1}, t_j) (u1,u2,t1),(u2,u3,t2),......,(uj,uj+1,tj),其中, t 1 , ≤ t 2 , ≤ t 3 . . . ≤ t j t_1, \leq t_2, \leq t_3 ... \leq t_j t1,≤t2,≤t3...≤tj。
从定义可以看出,只要按时间顺序在点与点之间游走即可,并不用关注在某个节点上停留了多久。基于时序游走的概念,就可以定义随机时序游走,即按照时序游走的概念,随机地在时序图上形成的路径,路径上边的时间是顺序增长的。有了随机时序游走的路径,既然是随机地,那么就需要给出概率值。下面就给出了计算随机时序游走的概率的方法。
基本思路是,在 ( v , u , t 1 ) (v, u, t_1) (v,u,t1)时,随机从 u u u走到 x x x的路径 ( u , x , t 2 ) (u, x, t_2) (u,x,t2)的概率 P [ ( u , x , t 2 ) ∣ ( v , u , t 1 ) ] P[(u, x, t_2)|(v, u, t_1)] P[(u,x,t2)∣(v,u,t1)]的值会随着 ( t 2 − t 1 ) (t_2-t_1) (t2−t1)的增加而减少。数学表达式:
P [ ( u , x , t 2 ) ∣ ( v , u , t 1 ) ] = β ∣ Γ u ∣ P[(u, x, t_2)|(v, u, t_1)]=\beta^{|\Gamma_u|} P[(u,x,t2)∣(v,u,t1)]=β∣Γu∣
其中, β ∈ ( 0 , 1 ] \beta \in (0,1] β∈(0,1]是转移概率, Γ u \Gamma_u Γu是在时间区间 t ′ ∈ [ t 1 , t 2 ] t' \in [t_1, t_2] t′∈[t1,t2]内,从节点 u u u发出的边的集合, Γ u = { ( u , y , t ′ ) ∣ t ′ ∈ [ t 1 , t 2 ] , y ∈ V } \Gamma_u = \{(u, y, t')\space|\space t'\in[t_1, t_2],y\in V\} Γu={ (u,y,t′) ∣ t′∈[t1,t2],y∈V}。
按照这个公式, β \beta β越小,随机游走在度的值非常高的节点停止的可能性越大。但是说收敛会慢,这个有点怪。难道不是停止越快,收敛越快吗?这里“收敛”是啥意思啊?
根据上对于时序随机游走的定义,可以看出如果我们游走的时间是无限大,即 t → ∞ t \rarr \infin t→∞,则整个时序图的PageRank就变成了一个静态图。具体的证明就不再讲了。
时序PageRank是在时序增强图上的PageRank方法。时序增强图的含义是在每个时间点 t 1 , t 2 , … , t i t_1, t_2, \dots, t_i t1,t2,…,ti存在的图。如下图所示:
时序PageRank的定义
根据上面的一系列定义,下面给出对时序PageRank的数学定义:
r ( u , t ) = ∑ v ∈ V ∑ k = 0 t ( 1 − α ) α k ∑ z ∈ Z ( v , u ∣ t ) P [ z ∣ t ] r(u, t)=\displaystyle \sum_{v\in V} \sum_{k=0}^t (1-\alpha)\alpha^k \sum_{z\in Z(v, u|t)} P[z|t] r(u,t)=v∈V∑k=0∑t(1−α)αkz∈Z(v,u∣t)∑P[z∣t]
其中, Z ( v , u ∣ t ) Z(v, u|t) Z(v,u∣t)是在时间 t t t过程中,从节点 v v v到 u u u的所有可能的时序游走的集合。而 α \alpha α则是开始一个新的游走的概率。
根据这个定义可以得到,如果 t → ∞ t \rarr \infin t→∞,则时序PageRank就变成了一个静态的PageRank。因为时间变成无限长后,整个图里,游走的概率就确定了。
时序PageRank还有一个变形,即时序个性化PageRank。这里面在上面公式里 ( 1 − α ) α k (1-\alpha)\alpha^k (1−α)αk后面加了一个个性化权重。具体就不多说了。
上面公式里需要进一步定义的是 P [ z ∣ t ] P[z|t] P[z∣t]。它是对于某个特别的游走 z ∈ Z ( v , u ∣ t ) z\in Z(v, u|t) z∈Z(v,u∣t)的概率。具体的方法是:
P [ z ∈ Z ( v , u ∣ t ) ] = c ( z ∣ t ) ∑ z ′ ∈ Z ( v , x ∣ t ) , x ∈ Z , ∣ z ′ ∣ = ∣ z ∣ C ( z ′ ∣ t ) P[z\in Z(v, u|t)] = \dfrac{c(z|t)}{\sum_{z'\in Z(v,x|t), x\in Z, |z'|=|z|} C(z'|t)} P[z∈Z(v,u∣t)]=∑z′∈Z(v,x∣t),x∈Z,∣z′∣=∣z∣C(z′∣t)c(z∣t)
其中, c ( z ∣ t ) = ( 1 − β ) ∏ ( ( u i , u i + 1 , t i + 1 ) ∣ ( u t − 1 , u i , t i ) ) ∈ Z β ∣ Γ u i ∣ c(z|t)=(1-\beta)\displaystyle \prod_{((u_i, u_{i+1}, t_{i+1})|(u_{t-1}, u_i, t_i))\in Z} \beta^{|\Gamma_{u_i}|} c(z∣t)=(1−β)((ui,ui+1,ti+1)∣(ut−1,ui,ti))∈Z∏β∣Γui∣。里面的 β \beta β是游走的停止概率。
具体的时序PageRank算法的伪代码如下:

具体的算法实现倒是不太复杂。就没仔细看了。
中观尺度
B站里下载的视频,第16课的结尾只讲到了PPT的第二部分,对于第三部分——中观尺度的演进,没有讲。下面就是我根据PPT的理解了。
中观尺度的网络演进要研究的问题主要就是:
- 网络节点的交互的模式是如何随时间变化的?
- 我们能从时序上模式的改变推断出网络有什么变化?
从图的结构上来看,中观尺度就是Motif这种大小级别上的图结构。所以从时间维度上来看,就是在不同的时间点,Motif的结构如何变化,以及不同结构的Motif的数量有什么改变。
时序Motif(Temporal Motif)
时序Motif的定义如下:
k k k个节点, l l l条边, δ \delta δ时序Motif是一系列共 l l l条边 ( u 1 , v 1 , t 1 ) , ( u 2 , v 2 , t 2 ) , … , ( u l , v l , t l ) (u_1, v_1, t_1),(u_2, v_2, t_2), \dots, (u_l, v_l, t_l) (u1,v1,t1),(u2,v2,t2),…,(ul,vl,tl)。其中, t 1 < t 2 < ⋯ < t l t_1 \lt t_2 \lt \dots \lt t_l t1<t2<⋯<tl而且 t l − t 1 ⩽ δ t_l - t_1 \leqslant \delta tl−t1⩽δ。 由这些边构成的最终静态导出一共包括 k k k个点。
研究时序Motif可以帮助发现网络演进的模式,比如发现趋势以及异常。下图里面给出了符合上面定义的3个点的一种Motif的例子。

有了时序Motif的定义,相应地可以完成多个任务。课程里面给出了多个案例研究,这里就不再详细记录。
从开始看第16课到现在有了2个多月了。发现近期无法按照之前的想法把224W的课看的那么的仔细了,因为对实际的业务问题,目前看完全看懂每个细节,并不能提供帮助。同时这门课也是基础课,追求的面广,但不深,因此很多内容可能未必会用的上,能理解和记忆最好,不行的话影响也不大。所以决定换一种方法,以快速的总结可能内容为主,不再追求每个细节的完全理解。先把整个课程过一遍。