优化算法|蚁群算法的理解及实现

1. 蚁群算法背景介绍

蚁群算法（Ant Colony Algorithm, ACA）由Marco Dorigo于1992年提出。
蚁群算法是一种群智能算法，它是由一群无智能或有轻微智能的个体（Agent）通过相互协作而表现出智能行为，从而为求解复杂问题提供了一个新的可能性。
在自然界中，蚂蚁觅食过程中，蚁群总能够按照寻找到一条从蚁巢和食物源的最优路径。下图显示了这样一个觅食的过程。

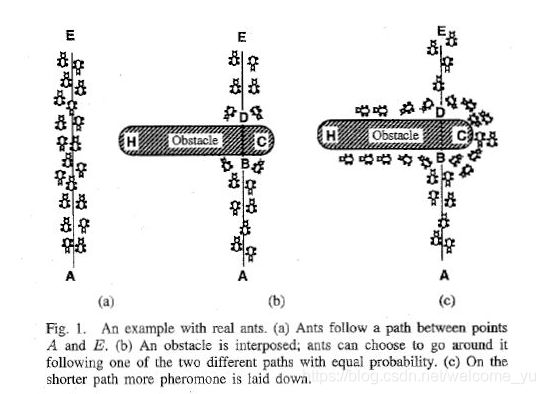
2.蚁群算法基本原理

蚁群算法的基本原理来源于自然界觅食的最短路径原理。根据昆虫学家的观察，蚂蚁可以在没有任何提示的情况下找到从食物源到巢穴的最短路径，并且能在环境发生变化(如原有路径上有了障碍物)后,自适应地搜索新的最佳路径。
蚂蚁是怎么做到这一点的呢？
蚁群算法有自己的优化策略：正反馈的信息机制、信息素浓度的更新、蚂蚁对能够访问的路径的筛选。

3.蚁群算法的计算过程

4. 模型构建

蚁群算法最早用来求解TSP问题，（Travel Salesperson Problem，即旅行商问题或者称为中国邮递员问题），因为它分布式特性，鲁棒性强并且容易与其它算法结合，但是同时也存在这收敛速度慢，容易陷入局部最优（local optimal）等缺点。
1）路径构建
AS中的随机比例规则；对于每只蚂蚁k，路径记忆向量R^k.按照访问顺序记录了所有k已经经过的城市序号。设蚂蚁k当前所在城市为i,则其选择城市j作为下一个访问对象的概率为:

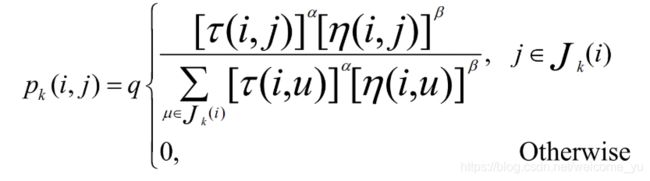
2）信息素更新

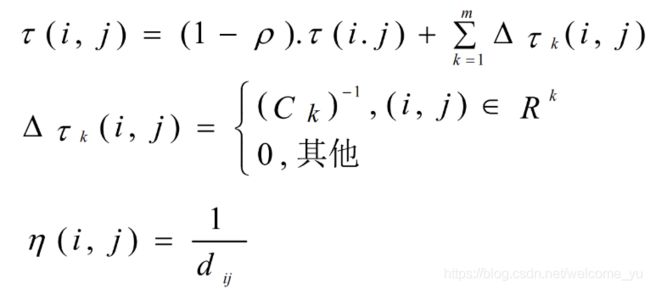
这里m是蚂蚁个数, ρ是信息素的蒸发率，规定0≤ ρ≤1，在AS中通常设置为 ρ =0.5，Δτij是第k只蚂蚁在它经过的边上释放的信息素量，它等于蚂蚁k本轮构建路径长度的倒数。C^{k表示路径长度，它是R}k中所有边的长度和。
构建图：构建图与问题描述图是一致的，成份的集合C对应着点的集合（即：C=N），连接对应着边的集合（即L=A）,且每一条边都带有一个权值，代表点i和j之间的距离。
约束条件：所有城市都要被访问且每个城市最多只能被访问一次。
信息素和启发式信息：TSP 问题中的信息素表示在访问城市i后直接访问城市j的期望度。启发式信息值一般与城市i和城市j的距离成反比。
解的构建：每只蚂蚁最初都从随机选择出来的城市出发，每经过一次迭代蚂蚁就向解中添加一个还没有访问过的城市。当所有城市都被蚂蚁访问过之后，解的构建就终止。
大致流程如下：

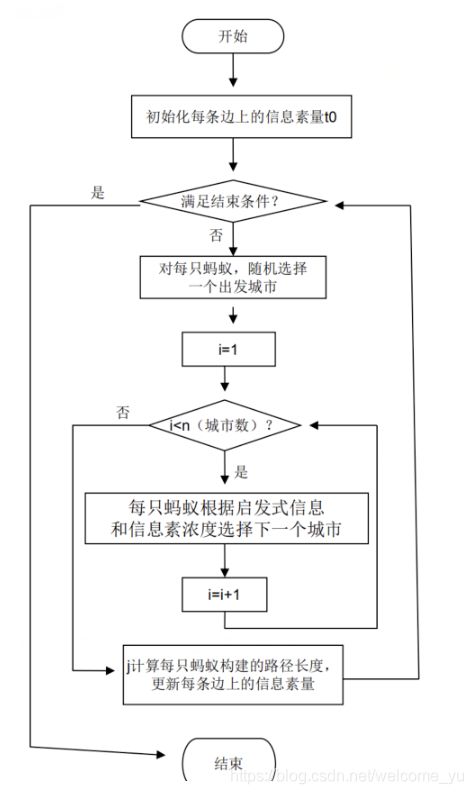
5. 蚁群算法matlab实现

% 蚁群算法找最大值
% 核心思路: 
% 和粒子群算法有些相似，都是靠团队的力量共同去找目标！
% 蚁群算法中特殊的是它的"信息素"挥发! 这个效果是其他算法中没有的！

clc;
clear;
% f的最大值就是-前面的数值;这里是2.4
f = inline('2.4-(x.^4 + 3*y.^4 - 0.2*cos(3*pi*x) - 0.4*cos(4*pi*y) + 0.6)');
x = -1:0.001:1;
y = -1:0.001:1;
[X,Y] = meshgrid(x,y);
F = f(X,Y);
figure(1);
mesh(X,Y,F);
xlabel('横坐标x'); ylabel('纵坐标y'); zlabel('空间坐标z');
hold on;

% 坐标/搜索范围的设置:
lower_x = -1;
upper_x = 1;
lower_y = -1;
upper_y = 1; 

% 模型初始参数设置:
ant = 80;      % 蚂蚁总数300只太多了,不到100只松松解决问题
times = 30;    % 每只蚂蚁搜寻80次
rou = 0.9;     % 信息素挥发速率
p0 = 0.2;      % 蚂蚁转移的概率常数

% 初始蚂蚁位置(空间内随机)、适应度计算:
ant_x = zeros(1,ant);  % 每只蚂蚁位置的x坐标
ant_y = zeros(1,ant);  % 每只蚂蚁位置的y坐标
tau = zeros(1,ant);    % 适应度/函数数值
Macro = zeros(1,ant);  % Macro和tau共同使用的中间过渡量而已
for i=1:ant
    ant_x(i) = (upper_x-lower_x)*rand() + lower_x;
    ant_y(i) = (upper_y-lower_y)*rand() + lower_y;
    tau(i) = f(ant_x(i),ant_y(i));         % 初始适应度/函数值
    plot3(ant_x(i),ant_y(i),tau(i),'k*');  % 起始群都用黑色*标记
    hold on;
    Macro = zeros(1,ant);
end

fprintf('蚁群搜索开始(找最大值):\n');
T = 1;
tau_best = zeros(1,times);  % 记录每轮寻找后的群体中的最大值!
p = zeros(1,ant);   % 每只蚂蚁状态转移的概率,都与p0比较
while T < times
    lamda = 1/T;
    % 这里是查看极值的地方!！
    [tau_best(T),bestindex] = max(tau);
    
    % 精度足够高，提前结束!
    % 这里我有个策略: 当前适应度值 与 前两轮的值对比！而不是与上一轮值对比！
    % 因为相邻两次循环的值很可能因为有一定的相关性而彼此接近！
    if T >= 3 && abs((tau_best(T) - tau_best(T-2))) < 0.000001
        fprintf('精度足够高,提前结束!\n');
        % 小心思:最后一次画图放在这里，可以把最后一个点标成蓝色而不是红色！
        plot3(ant_x(bestindex), ant_y(bestindex), f(ant_x(bestindex),ant_y(bestindex)), 'b*');
        break;
    end
    plot3(ant_x(bestindex), ant_y(bestindex), f(ant_x(bestindex),ant_y(bestindex)), 'r*');
    hold on;
    
    for i = 1:ant
        p(i) = (tau(bestindex) - tau(i))/tau(bestindex); % 每一只蚂蚁的转移概率
    end
    % 位置更新: 新算的临时坐标tempx与tempy不一定用!
    for i = 1:ant
        % 小于p0进行局部搜索:
        if p(i) < p0
            tempx = ant_x(i) + (2*rand-1)*lamda;
            tempy = ant_y(i) + (2*rand-1)*lamda;
        % 大于p0进行全局搜索:
        else
            tempx = ant_x(i) + (upper_x-lower_x)*(rand-0.5);
            tempy = ant_y(i) + (upper_y-lower_y)*(rand-0.5);
        end
        % 不能越界，做一个越界判断:
        if tempx < lower_x
            tempx = lower_x;
        end
        if tempx > upper_x
            tempx = upper_x;
        end
        if tempy < lower_y
            tempy = lower_y;
        end
        if tempy > upper_y
            tempy = upper_y;
        end
        % 判断蚂蚁是否移动,即tempx和tempy是否采用
        % tau(i)是上一轮的值；Macro是及时更新的值!!
        if f(tempx,tempy) > tau(i)
            ant_x(i) = tempx;
            ant_y(i) = tempy;
            Macro(i) = f(tempx,tempy);
        end
    end
   
    % 适应度更新:
    for i = 1:ant
        tau(i) = (1-rou)*tau(i) + Macro(i);
    end
    
    % 搜索进入下一轮:
    T = T + 1;
end
hold off;
    
fprintf('蚁群搜索到的最大值点:(%.5f,%.5f,%.5f)\n',...
        ant_x(bestindex), ant_y(bestindex), f(ant_x(bestindex),ant_y(bestindex)));
fprintf('搜索次数:%d\n',T)

运行结果展示：

6.算法分析

蚁群算法(AS)的缺点：

1、收敛速度慢（运行一次要等好久）

2、易于陷入局部最优

蚁群算法在解决小规模TSP问题是勉强能用，稍加时间就能发现最优解，但是若问题规模很大，蚁群算法的性能会极低，甚至卡死。所以可以进行改进，例如精英蚂蚁系统。

参考：

参考1：https://mp.weixin.qq.com/s?__biz=MzI0NzU3ODU5OA==&mid=2247484401&idx=1&sn=41d385f29f24887e06a0f256892560a3&chksm=e9aca978dedb206e33d569bd5150ee3222dd0c536ee172dbb0058ea0d081d849913dd34720ee&scene=21#wechat_redirect
参考2：https://zhuanlan.zhihu.com/p/137408401
参考3：https://www.cnblogs.com/bokeyuancj/p/11798635.html