0-1背包的几种解法

题目

	有n个物品，它们有各自的体积和价值，现有给定容量的背包，
	如何让背包里装入的物品具有最大的价值总和？

方法

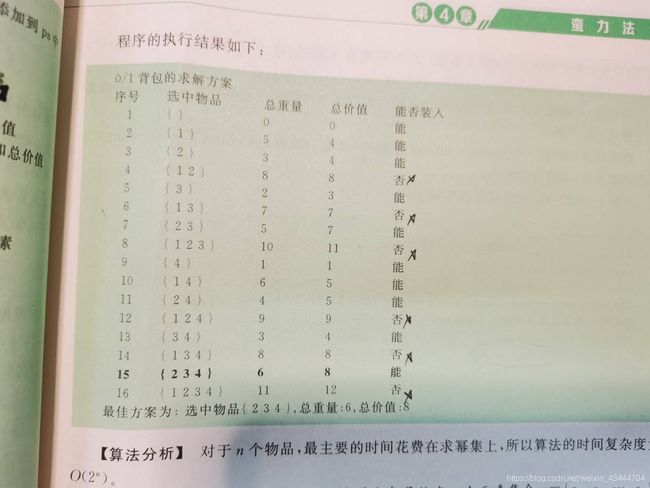
暴力

	使用密集来遍历所有的情况，像密集是[1,2,3]就是选择1,2,3个背包。
	当是[1,2]，就是选择1,2个背包。

#include
#include
using namespace std;
vector<vector<int>>ps;
//求幂积，插入法。
void PSet(int n)//上一个blog的增量法求密集
{
     
    vector<vector<int>>ps1;
    vector<vector<int>>::iterator it;
    vector<int>s;
    ps.push_back(s);
    for(int i=1;i<n;i++)
    {
     
        ps1=ps;
        for(it=ps1.begin();it!=ps1.end();++it)
        {
     
            (*it).push_back(i);
        }
        for(it=ps1.begin();it!=ps1.end();++it)
        {
     
            ps.push_back(*it);
        }
    }
}
int Knap(int *w,int *v,int W)//就是对照着密集，遍历所有的情况。
{
     
    int maxWeight,maxV;//最大价值时候的质量
    int sumw,sumv;//当前情况的总质量和总价值
    vector<vector<int>>::iterator it;
    vector<int>::iterator sit;
    for(it=ps.begin();it!=ps.end();++it)//遍历每一种情况
    {
     
        sumv=0;//先初始为0。
        sumw=0;
        for(sit=(*it).begin();sit!=(*it).end();++sit)
        {
     
            sumw+=w[*sit-1];//从0开始加
            sumv+=v[*sit-1];
        }
        if(sumw<=W)//如果总质量没有超过背包的总质量。就阔以
        {
     
            if(sumv>maxV)//记录符合要求的最大价值
            {
     
                maxV=sumv;
                maxWeight=sumw;
            }
        }
    }
    return maxV;
}
int main()
{
      
    int n=5;
    int w[]={
     5,3,2,1};
    int v[]={
     4,4,3,1};
    int W=6;
    PSet(n);
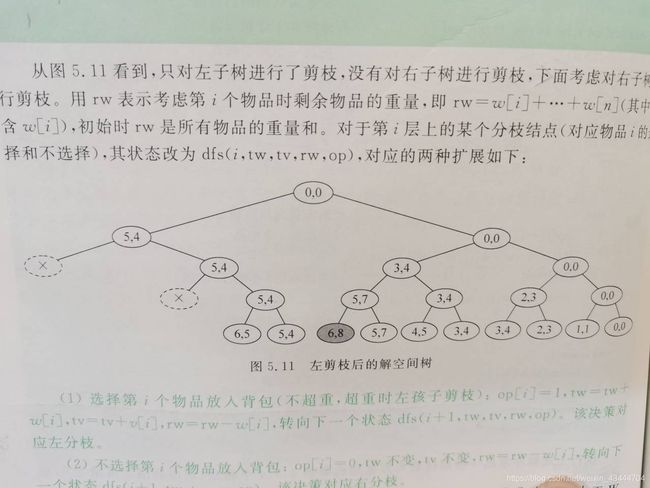
    cout<<Knap(w,v,W);
}

回溯

	使用dfs。上硬图。dfs的参数设计很巧妙，
	第一个i代表着当前正在对第几个物品做出选择，当i>n就直接跳出，因为已经选择完了。
	tw，tv分别是当前重量，当前质量。
	rw剩余质量，用来标识特殊情况
	op[]记录选择情况。

#include
using namespace std;
#define MAXN 20
int n=4;//四种物品
int W=6;
int w[]={
     0,5,3,2,1};//重量。
int v[]={
     0,4,4,3,1};//装入的价值。
int x[MAXN];
int maxv=0;//当前最大价值。
void dfs(int i,int tw,int tv,int rw,int op[])//rw是剩下的量。
{
     
    if(i>n)//出口，当i大于n说明已经装了四个物品了。
    {
     
        if(tv>maxv&&tw<=W)//符合要求就记住选项。
        {
     
           maxv=tv;
            for(int j=0;j<=n;j++)
            {
     
                x[j]=op[j];
            }
        }
    }

    else
    {
     
        if(tw+w[i]<=W)//左孩子剪枝。当加上这个w[i]重量超过， 那肯定是没有用的。
        {
     
            op[i]=1;//取第i个。
            dfs(i+1,tw+w[i],tv+v[i],rw-w[i],op);//重量加上，价值加上，剩余重量减少。
        }
        op[i]=0;//不选这个。
        dfs(i+1,tw,tv,rw-w[i],op);//剩余重量减少。
        // if(rw+tw-w[i]>=W)//右孩子剪枝。当题目要求是必须要恰好装满背包就有这个剪枝。
        // {
     
        //      op[i]=0;//0代表不选择。
        //      dfs(i+1,tw,tv,rw-w[i],op);
        // }
        
    }
}
int main()
{
     
    int op[MAXN];
    dfs(1,0,0,15,op);
    cout<<maxv<<endl;
}

搞不动了搞不动了

，，，，，，，，，，，，，，，，，，，，，，，，，，，，，

分支界限

动态规划