基于旋量理论的六轴机器人建模
机器人建模(Screw Method)
如上图所示首先在参考坐标系下,按照机械臂的关节运动正方向确定Z轴,之后通过用户方便自定义其余的X轴和Y轴。这里和D-Hc参数法最大的不同在于不需要按照固定的建模方式建立坐标系,只要确定基坐标系,其余的都可以按照自行自定义的方式进行确定。
六轴机械臂参数
首先需要确定所有机械臂的自身关节参数:
| i | x i x_i xi | y i y_i yi | z i z_i zi |
|---|---|---|---|
| 1 | 0.000 | 0.000 | 0.182 |
| 2 | 0.040 | 0.000 | 0.160 |
| 3 | 0.000 | 0.000 | 0.275 |
| 4 | 0.280 | 0.000 | 0.025 |
| 5 | 0.000 | 0.000 | 0.000 |
| 6 | 0.000 | 0.000 | 0.000 |
| T | 0.073 | 0.000 | 0.000 |
其中,需要注意的是末端坐标系中作为第六关节轴可以附加一些末端执行器。例如,夹爪,法兰等等。所以可以在最后的坐标系变换中从第六关节轴可以加一个坐标变换至末端执行器的坐标系中。
螺旋轴 S i = ( ω i , v i ) , i = 1 , 2 , . . . , 6 S_i=(\omega_i,v_i),i=1,2,...,6 Si=(ωi,vi),i=1,2,...,6,螺旋轴以及线速度等等坐标如下表所示:
| i | ω i \omega_i ωi | v i v_i vi |
|---|---|---|
| 1 | [ 0 0 1 ] \begin{bmatrix}0&0&1\end{bmatrix} [001] | [ 0 0 0 ] \begin{bmatrix}0&0&0\end{bmatrix} [000] |
| 2 | [ 0 1 0 ] \begin{bmatrix}0&1&0\end{bmatrix} [010] | [ − ( z 1 + z 2 ) 0 x 2 ] \begin{bmatrix}-(z_1+z_2)&0&x_2\end{bmatrix} [−(z1+z2)0x2] |
| 3 | [ 0 1 0 ] \begin{bmatrix}0&1&0\end{bmatrix} [010] | [ − ( z 1 + z 2 + z 3 ) 0 x 2 ] \begin{bmatrix}-(z_1+z_2+z_3)&0&x_2\end{bmatrix} [−(z1+z2+z3)0x2] |
| 4 | [ 1 0 0 ] \begin{bmatrix}1&0&0\end{bmatrix} [100] | [ 0 z 1 + z 2 + z 3 + z 4 0 ] \begin{bmatrix}0&z_1+z_2+z_3+z_4&0\end{bmatrix} [0z1+z2+z3+z40] |
| 5 | [ 0 1 0 ] \begin{bmatrix}0&1&0\end{bmatrix} [010] | [ − ( z 1 + z 2 + z 3 + z 4 ) 0 x 2 + x 4 ] \begin{bmatrix}-(z_1+z_2+z_3+z_4)&0&x_2+x_4\end{bmatrix} [−(z1+z2+z3+z4)0x2+x4] |
| 6 | [ 1 0 0 ] \begin{bmatrix}1&0&0\end{bmatrix} [100] | [ 0 z 1 + z 2 + z 3 + z 4 0 ] \begin{bmatrix}0&z_1+z_2+z_3+z_4&0\end{bmatrix} [0z1+z2+z3+z40] |
算例验证
验证手段用的是正运动学验证,就是通过给定多个关节角度,用已知正确的D-H参数法建立的机器人进行验证。在运动学中需要用到指数积公式以及指数矩阵或罗德里格公式。首先对指数矩阵进行讲解,若是有了解过现代控制理论或者相应的数学知识将会对指数矩阵有所了解,可以跳过此部分。
矩阵指数: e A t e^{At} eAt是用来对先行常微分方程求解后得到的一个矩阵,其中A是一个已知的矩阵。对该矩阵指数进行泰勒展开可以得到:
e A t = I + A t + ( A t ) 2 2 ! + ( A t ) 3 3 ! + ⋯ e^{At}=I+At+\frac{(At)^{2}}{2!}+\frac{(At)^{3}}{3!}+\cdots eAt=I+At+2!(At)2+3!(At)3+⋯
在给定的螺旋轴,也就是旋转轴的情况下需要先将其映射至 R 3 × 3 R^{3\times3} R3×3中获得矩阵。所以用到了反对称矩阵用[ ]表示。之后就可以通过矩阵指数公式获得:
e ω ^ t = I + [ ω ^ ] θ + [ ω ^ ] 2 θ 2 2 ! + [ ω ^ ] 3 θ 3 3 ! + ⋯ = I + ( θ − θ 3 3 ! + θ 5 5 ! − ⋯ ) [ ω ^ ] + ( θ 2 2 ! − θ 4 4 ! + θ 6 6 ! + ⋯ ) [ ω ^ ] e^{\hat{\omega}t}=I+[\hat{\omega}]\theta+[\hat\omega]^2\frac{\theta^2}{2!}+[\hat\omega]^3\frac{\theta^3}{3!}+\cdots\\=I+(\theta-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}-\cdots)[\hat{\omega}]+(\frac{\theta^2}{2!}-\frac{\theta^4}{4!}+\frac{\theta^6}{6!}+\cdots)[\hat{\omega}] eω^t=I+[ω^]θ+[ω^]22!θ2+[ω^]33!θ3+⋯=I+(θ−3!θ3+5!θ5−⋯)[ω^]+(2!θ2−4!θ4+6!θ6+⋯)[ω^]
[罗德里格斯公式]:表示绕物体坐标系的旋转轴一定角度后的姿态
假设给定了一定向量 ω ^ θ ∈ R 3 \hat\omega\theta\in R^3 ω^θ∈R3,其中 θ \theta θ为任意角度是一个标量,而 ω ^ ∈ R 3 \hat\omega\in R^3 ω^∈R3为一个单位向量,表征基坐标系下的旋转轴,则公式为:
R o t ( ω ^ , θ ) = e [ ω ^ ] θ = I + s i n θ [ ω ^ ] + ( 1 − c o s θ ) [ ω ^ ] ∈ S O ( 3 ) Rot(\hat\omega,\theta)=e^{[\hat\omega]\theta}=I+sin\theta[\hat\omega]+(1-cos\theta)[\hat\omega]\in SO(3) Rot(ω^,θ)=e[ω^]θ=I+sinθ[ω^]+(1−cosθ)[ω^]∈SO(3)
-
当机器人处于初始位置时,末端位姿 M ∈ S E ( 3 ) M\in SE(3) M∈SE(3)
-
当机器人处于初始位置时,相对于基坐标系的螺旋轴 S 1 , S 2 , ⋯ , S n S_1,S_2,\cdots,S_n S1,S2,⋯,Sn对应各个关节的螺旋旋量其中 S i = [ ω i , v i ] S_i=[\omega_i,v_i] Si=[ωi,vi]
-
关节变量 ( θ 1 , θ 2 , ⋯ , θ n ) (\theta_1,\theta_2,\cdots,\theta_n) (θ1,θ2,⋯,θn)
T ( θ ) = e [ S 1 ] θ 1 e [ S 2 ] θ 2 ⋯ e [ S n ] θ n M T(\theta)=e^{[S_1]\theta_1}e^{[S_2]\theta_2}\cdots e^{[S_n]\theta_n}M T(θ)=e[S1]θ1e[S2]θ2⋯e[Sn]θnM
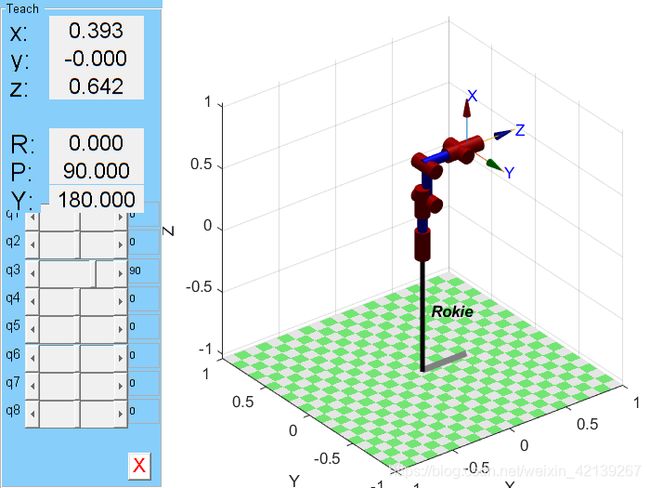
在上述基础上我们首先对关节变量为 θ = ( 0 0 0 0 0 0 ) \theta=(0\space0\space0\space0\space0\space0) θ=(0 0 0 0 0 0)情况下进行验证,首先用机器人工具包进行验证。
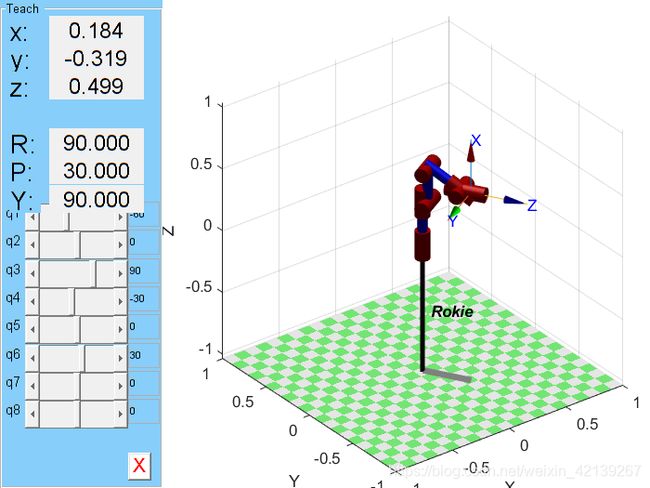
从末端位置可以看出正确。为了防止姿态上出现错误,关节变量为 θ = ( − π 3 0 π 6 0 − π 6 0 ) \theta=(-\frac{\pi}{3}\space0\space\frac{\pi}{6}\space 0 \space -\frac{\pi}{6}\space 0) θ=(−3π 0 6π 0 −6π 0)
需要注意的是,两种建模方式不同,导致各个关节的正方向不同,所以在建立关节坐标系过程中第二种方法容错率更大,重建也更为方便。
GitHub程序地址:https://github.com/MingshanHe/RobotArm.git
微信公众号:
邮箱:[email protected]