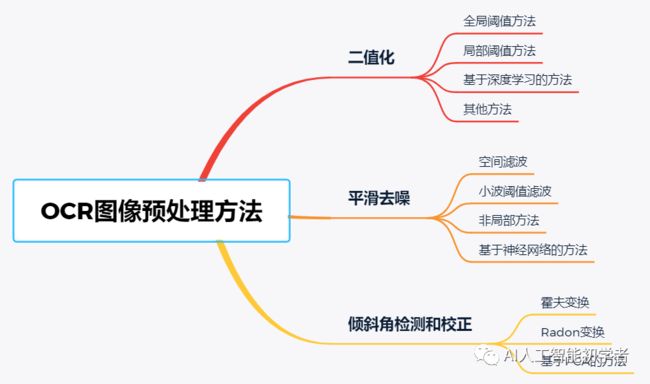
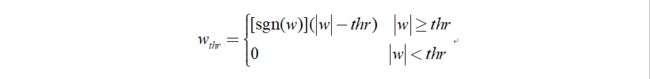『OCR深度实践』OCR学习笔记(2)：图像预处理

1. 『OCR深度实践』OCR学习笔记(1)：绪论

---

二、图像预处理

2.1 二值化

1. 定义： 图像的二值化，就是将图像上的像素点的灰度值设置为 0 或 255，也就是将整个图像呈现出明显的只有黑和白的视觉效果。
2. 优势： 一方面减少了数据维度，另一方面通过排除原图中噪声带来的干扰，可以凸显有效区域的轮廓结构。

2.1.1 全局阈值方法

2.1.1.1 固定阈值方法

该方法是对于输入图像中的所有像素点统一使用同一个固定阈值。
主要缺陷：很难为不同的输入图像确定最佳阈值。

import cv2
import numpy as np
from tqdm import tqdm

image = cv2.imread("peng.png",0)
h = image.shape[0]
w = image.shape[1]

## 唯一确定阈值
a = 150
new_image = np.zeros((h,w),np.uint8)
for i in tqdm(range(h)):
    for j in range(w):
        if(image[i,j]> a ):
            new_image[i,j] = 255
        else:
            new_image[i,j] = 0

cv2.imshow("new",new_image)
cv2.waitKey()

2.1.1.2 OTSU 阈值方法（基于直方图）

OTSU 算法又称为 最大类间方差法；
基本原理： 用一个阈值将图像中的数据分为两类，一类中图像的像素点的灰度均小于这个阈值，另一类中的图像的像素点的灰度均大于或者等于该阈值。如果这两个类中像素点的灰度的方差越大，说明获取到的阈值就是最佳的阈值。（底层原理才疏学浅，不知道怎么表述）

import cv2
import os
import numpy as np
import pandas as pd
from tqdm import tqdm

### 大津法
def otsu(image):
    h = image.shape[0]
    w = image.shape[1]
    m = h*w
    otsuimg = np.zeros((h, w), np.uint8)
    initial_threshold = 0
    final_threshold   = 0
    # 初始化各灰度级个数统计参数
    histogram = np.zeros(256, np.int32)
    # 初始化各灰度级占图像中的分布的统计参数
    probability = np.zeros(256, np.float32)

    ### 各个灰度级的个数统计
    for i in tqdm(range(h)):
        for j in range(w):
            s = image[i,j]
            histogram[s] = histogram[s] +1
    ### 各灰度级占图像中的分布的统计参数
    for i in tqdm(range(256)):
        probability[i] = histogram[i]/m

    for i in tqdm(range(255)):
        w0 = w1 = 0  ## 前景和背景的灰度数
        fgs = bgs = 0  # 定义前景像素点灰度级总和背景像素点灰度级总和
        for j in range(256):
            if j <= i:  # 当前i为分割阈值
                w0 += probability[j]  # 前景像素点占整幅图像的比例累加
                fgs += j * probability[j]
            else:
                w1 += probability[j]  # 背景像素点占整幅图像的比例累加
                bgs += j * probability[j]
        u0 = fgs / w0  # 前景像素点的平均灰度
        u1 = bgs / w1  # 背景像素点的平均灰度
        G  = w0*w1*(u0-u1)**2
        if G >= initial_threshold:
            initial_threshold = G
            final_threshold = i
    print(final_threshold)

    for i in range(h):
        for j in range(w):
            if image[i, j] > final_threshold:
                otsuimg[i, j] = 255
            else:
                otsuimg[i, j] = 0
    return otsuimg

### 首先将图片转化为灰度图像
image = cv2.imread("***.png")
gray = cv2.cvtColor(img,cv2.COLOR_RGB2GRAY)

# 方法一：原理代码实现
otsuimage  = otsu(gray)

# 方法二：OpenCV 函数实现
ret, binary = cv2.threshold(gray, 0, 255, cv2.THRESH_OTSU)
print('threshold value: ', ret)
cv2.imshow('binary', binary)

2.1.2 局部阈值方法

2.1.2.1 自适应阈值算法

主要思想： 以一个像素点为中心设置 s*s 的滑窗，滑窗扫过整张图片，每次扫描均对窗口内的像素求均值并将均值作为局部阈值。它的思想不是计算全局图像的阈值，而是根据图像不同区域亮度分布，计算其局部阈值，所以对于图像不同区域，能够自适应计算不同的阈值，因此被称为自适应阈值法。

adaptiveThreshold(
	src, 		# 原始灰度图像 
	maxValue, 	# 像素值上限
	adaptiveMethod, 	# 自适应方法
	thresholdType,		# 值的赋值方法
	blockSize, 	# 规定邻域大小（一个正方形的领域）
	C, 		# 阈值等于均值或者加权值减去这个常数（为0相当于阈值，就是求得领域内均值或者加权值）
	dst=None
)

自适应方法：

• cv2.ADAPTIVE_THRESH_MEAN_C：邻域内均值
• cv2.ADAPTIVE_THRESH_GAUSSIAN_C：邻域内像素点加权和，权重为一个高斯窗口
  
  

值的赋值方法：

• cv2.THRESH_BINARY
• cv2.THRESH_BINARY_INV

# 示例：
gray = cv2.cvtColor(image,cv2.COLOR_BGR2GRAY)
binary = cv2.adaptiveThreshold(gray,255,cv2.ADAPTIVE_THRESH_MEAN_C,cv2.THRESH_BINARY,25,10)

2.1.2.2 Niblack 算法

Niblack 算法同样是根据窗口内的像素值来计算局部阈值的，不同之处在于它不仅考虑到区域内像素点的均值和方差，还考虑到用一个事先设定的修正系数 k 来决定影响程度。

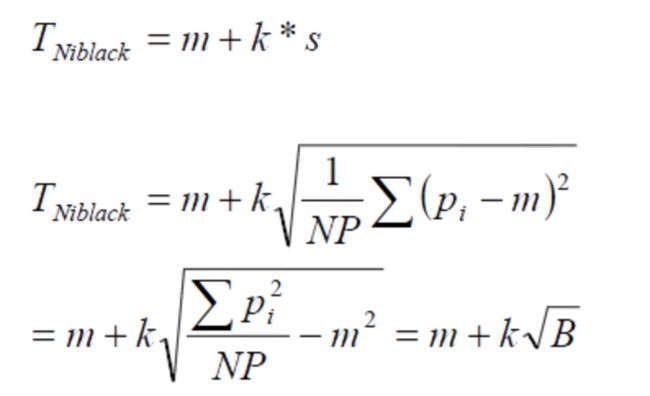
• T 是阈值，m 是图像邻域窗口的均值，s 是邻域窗口的标准差，K 是预先设定的修正值。
• Niblack法的优点：
  对每一个像素点都独立的根据此像素点的邻域的情况来计算门限，与 m(x,y) 相近的像素点被判定为背景，反之则为前景，而相近的程度则由标准差和修正系数来决定，这样做可以保证算法的灵活性。
• Niblack法的不足：
  由于要利用域 r×r 模板遍历图像，导致边界区域 (r-1)/2 的像素范围内无法求取阈值；同时当进行图像遍历时，如果域 r×r 范围内都是背景，经 Niblack 计算后必有一部分被确定为目标，产生伪噪声。因此，r 的选择非常关键，若窗口太小，则不能有效地抑制噪声；若窗口太大，则会导致细节丢失。
• 总之，用 Niblack 方法进行图像分割时，选择的处理模板窗口 r*r 大小的选择很关键，选择的空间太小，则噪声抑制的效果不理想，目标主体不够突出，选择的空间太大，则目标的细节会被去除而丢失信息。

2.1.2.3 Sauvola 算法

• Sauvola 算法的输入是灰度图像，它以当前像素点为中心，根据当前像素点邻域内的灰度均值与标准方差来动态计算该像素点的阈值。
• 假定当前像素点的坐标为 (x,y)，以该点为中心的领域为 r*r，g(x,y) 表示 (x,y) 处的灰度值，Sauvola 算法的步骤为：

step 1： 计算 r*r 邻域内的灰度均值 m(x,y) 与标准方差 s(x,y)；

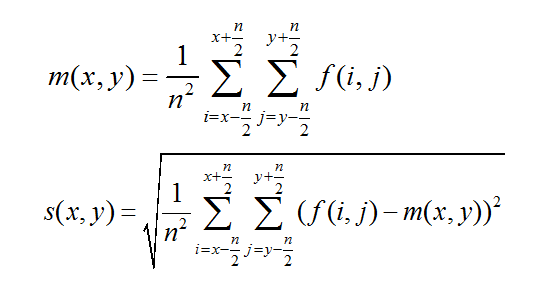
step 2： 计算像素点 (x,y) 的阈值 T(x,y)。

def integral(img):
    '''
    计算图像的积分和平方积分
    :param img:Mat--- 输入待处理图像
    :return:integral_sum, integral_sqrt_sum：Mat--- 积分图和平方积分图
    '''
    integral_sum = np.zeros((img.shape[0],img.shape[1]),dtype=np.int32)
    integral_sqrt_sum = np.zeros((img.shape[0],img.shape[1]),dtype=np.int32)
    rows,cols = img.shape
    for r in range(rows):
        sum = 0
        sqrt_sum = 0
        for c in range(cols):
            sum += img[r][c]
            sqrt_sum += math.sqrt(img[r][c])
            if r==0:
                integral_sum[r][c] = sum
                integral_sqrt_sum[r][c] = sqrt_sum
            else:
                integral_sum[r][c] = sum + integral_sum[r-1][c]
                integral_sqrt_sum[r][c] = sqrt_sum + integral_sqrt_sum[r-1][c]
    return integral_sum, integral_sqrt_sum
 
def sauvola(img,k=0.1,kernerl=(31,31)):
    '''
    sauvola阈值法。
    根据当前像素点邻域内的灰度均值与标准方差来动态计算该像素点的阈值
    :param img:Mat--- 输入待处理图像
    :param k:float---修正参数,一般0
    if kernerl[0]%2!=1 or kernerl[1]%2!=1:
        raise ValueError('kernerl元组中的值必须为奇数,'
                         '请检查kernerl[0] or kernerl[1]是否为奇数!!!')
 
    # 计算积分图和积分平方和图
    integral_sum,integral_sqrt_sum=integral(img)
    # integral_sum, integral_sqrt_sum = cv2.integral2(img)
    # integral_sum=integral_sum[1:integral_sum.shape[0],1:integral_sum.shape[1]]
    # integral_sqrt_sum=integral_sqrt_sum[1:integral_sqrt_sum.shape[0],1:integral_sqrt_sum.shape[1]]
 
    #创建图像
    rows,cols=img.shape
    diff=np.zeros((rows,cols),np.float32)
    sqrt_diff=np.zeros((rows,cols),np.float32)
    mean=np.zeros((rows,cols),np.float32)
    threshold=np.zeros((rows,cols),np.float32)
    std=np.zeros((rows,cols),np.float32)
 
    whalf=kernerl[0]>>1#计算领域类半径的一半
 
    for row in range(rows):
        print('第{}行处理中...'.format(row))
        for col in range(cols):
            xmin=max(0,row-whalf)
            ymin=max(0,col-whalf)
            xmax=min(rows-1,row+whalf)
            ymax=min(cols-1,col+whalf)
 
            area=(xmax-xmin+1)*(ymax-ymin+1)
            if area<=0:
                sys.exit(1)
 
            if xmin==0 and ymin==0:
                diff[row,col]=integral_sum[xmax,ymax]
                sqrt_diff[row,col]=integral_sqrt_sum[xmax,ymax]
            elif xmin>0 and ymin==0:
                diff[row, col] = integral_sum[xmax, ymax]-integral_sum[xmin-1,ymax]
                sqrt_diff[row, col] = integral_sqrt_sum[xmax, ymax]-integral_sqrt_sum[xmin-1, ymax]
            elif xmin==0 and ymin>0:
                diff[row, col] = integral_sum[xmax, ymax] - integral_sum[xmax, ymax-1]
                sqrt_diff[row, col] = integral_sqrt_sum[xmax, ymax] - integral_sqrt_sum[xmax, ymax-1]
            else:
                diagsum=integral_sum[xmax, ymax]+integral_sum[xmin-1, ymin-1]
                idiagsum=integral_sum[xmax, ymin-1]+integral_sum[xmin-1, ymax]
                diff[row,col]=diagsum-idiagsum
 
                sqdiagsum=integral_sqrt_sum[xmax, ymax]+integral_sqrt_sum[xmin-1, ymin-1]
                sqidiagsum=integral_sqrt_sum[xmax, ymin-1]+integral_sqrt_sum[xmin-1, ymax]
                sqrt_diff[row,col]=sqdiagsum-sqidiagsum
 
            mean[row,col]=diff[row, col]/area
            std[row,col]=math.sqrt((sqrt_diff[row,col]-math.sqrt(diff[row,col])/area)/(area-1))
            threshold[row,col]=mean[row,col]*(1+k*((std[row,col]/128)-1))
 
            if img[row,col]<threshold[row,col]:
                img[row,col]=0
            else:
                img[row,col]=255
 
    return img

2.1.3 基于深度学习的方法

2.1.3.1 使用全卷积的二值化方法

看了效果很不错，在公开的数据集中的表现性能很好，具体我还没有去复现，到时来补全。

2.1.4 基于图像处理的方法

实现的方法步骤主要如下：

1. 将 RGB 图像转为灰度图；
2. 图像滤波处理；
3. 数学形态学处理；
4. 阈值计算。

滤波：

• 维纳滤波(Wiener Filter)：又称为最小二值滤波器，是利用平稳随机过程的相关特性和频谱特性对混有噪声的信号进行滤波。
• 高斯滤波(Gaussian Filter)：是一种线性平滑滤波，适用于消除高斯噪声。
  
  

数学形态学：

• 通过从图像中提取对表达和描绘区域形状有意义的图像分量，使后续工作能够抓住目标对象最具区分性的形状特征。
• 基本运算包括：腐蚀、膨胀、开运算、闭运算

2.2 平滑噪声

• 图像噪声： 是指存在于图像数据中的不必要的或多余的干扰信息，产生于图像的采集、量化或传输过程，对图像的后处理、分析均会产生极大的影响。噪声的存在严重影响了图像的质量，因此在图像增强处理和分类处理之前，必须予以纠正。 图像中各种妨碍人们对其信息接受的因素即可称为图像噪声 。噪声在理论上可以定义为 “不可预测，只能用概率统计方法来认识的随机误差”。
• 平滑滤波： 是低频增强的空间域滤波技术。它的目的有两类：一类是 模糊；另一类是 消除噪音。空间域的平滑滤波一般采用简单平均法进行，就是求邻近像元点的平均亮度值。邻域的大小与平滑的效果直接相关，邻域越大平滑的效果越好，但邻域过大，平滑会使边缘信息损失的越大，从而使输出的图像变得模糊，因此需合理选择邻域的大小。

2.2.1 空间滤波

• 空间滤波是一种采用滤波处理的影像增强方法。其理论基础是空间卷积和空间相关。目的是改善影像质量，包括去除高频噪声与干扰，及影像边缘增强、线性增强以及去模糊等。分为 低通滤波（平滑化） 、高通滤波（锐化） 和 带通滤波。
• 空间滤波由一个邻域和对该邻域内像素执行的预定义操作组成，滤波器中心遍历输入图像的每个像素点之后就得到了处理后的图像。每经过一个像素点，邻域中心坐标的像素值就替换为预定义操作的计算结果。
• 若在图像像素上执行的线性操作，则该滤波器称为 线性空间滤波器，反之则称为 非线性空间滤波器。(PS： 后面的表述来源于一本书《基于深度学习的文字识别》)

2.2.1.1 线性空间滤波器

• 常见的有 平滑线性滤波器 和 高斯滤波器
• 平滑线性滤波器： 输出是包含在滤波器模板邻域内像素的简单平均值，因此也称为 均值滤波器；
• 高斯滤波器： 其模板系数随着与模板中心距离的增大而减小。

2.2.1.2 非线性空间滤波器

• 常见的有 中值滤波器 和 双边滤波器
• 中值滤波器： 首先是对邻域内的值进行排序，中值作为输出。该滤波器消除椒盐噪声的效果优于线性空间滤波器；
• 双边滤波器： 不仅如高斯滤波一样考虑到像素间的欧式距离，还关注到像素范围域中的辐射差异(如像素与中心点间的相似程度、颜色强度和深度距离等)，这两个权重域分别称为：空间域 和 像素范围域。
• 双边滤波器的好处是可以做 边缘保存（edge preserving），一般用高斯滤波去降噪，会较明显地模糊边缘，对于高频细节的保护效果并不明显。双边滤波器顾名思义比高斯滤波多了一个高斯方差sigma－d，它是基于空间分布的高斯滤波函数，所以在边缘附近，离的较远的像素不会太多影响到边缘上的像素值，这样就保证了边缘附近像素值的保存。但是由于保存了过多的高频信息，对于彩色图像里的高频噪声，双边滤波器不能够干净的滤掉，只能够对于低频信息进行较好的滤波。

######## 四个不同的滤波器 #########
img = cv2.imread('img/test.png')
# 平滑线性滤波滤波
img_mean = cv2.blur(img, (5, 5))
# 高斯滤波
img_Guassian = cv2.GaussianBlur(img, (5, 5), 0)
# 中值滤波
img_median = cv2.medianBlur(img, 5)
# 双边滤波
dst = cv2.bilateralFilter(src=image, d=0, sigmaColor=100, sigmaSpace=15)

2.2.2 小波阈值去噪

小波阈值去噪的实质为抑制信号中无用部分、增强有用部分的过程。小波阈值去噪过程为：

1. 分解过程，即选定一种小波对信号进行 n 层小波分解；
2. 阈值处理过程，即对分解的各层系数进行阈值处理，获得估计小波系数；
3. 重构过程，据去噪后的小波系数进行小波重构，获得去噪后的信号。
   
   

阈值的选择是离散小波去噪中最关键的一步，阈值处理函数分为 硬阈值 和 软阈值。

2.2.2.1 硬阈值函数

当小波系数的绝对值大于给定阈值时，小波系数不变；小于阈值时，小波系数置零。

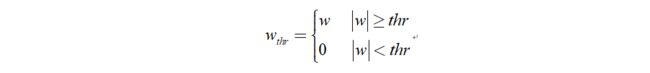
2.2.2.2 软阈值函数

当小波系数的绝对值大于给定阈值时，令小波系数减去阈值；小于阈值时，小波系数置零。

2.2.3 非局部方法

2.2.4 基于神经网络的方法

2.3 倾斜角检测和矫正

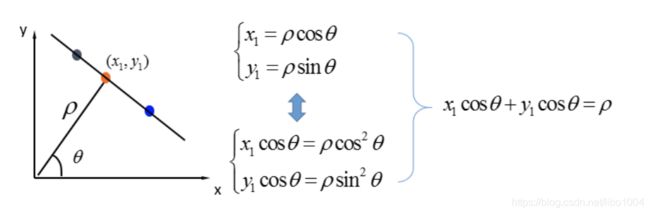
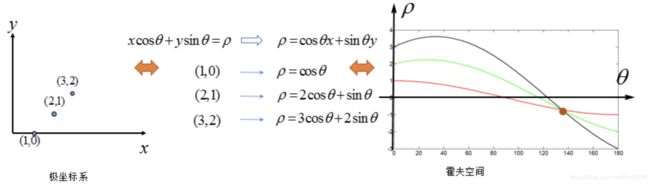
2.3.1 霍夫变换

原理：若直线坐标系中的点共线，那么它们在霍夫空间中对应的曲线也必然相交于一点。
霍夫变换的后处理的基本方式：选择由尽可能多直线汇成的点。

# 先通过 hough transform 检测图片中的图片，计算直线的倾斜角度并实现对图片的旋转
import os
import cv2
import math
import random
import numpy as np
from scipy import misc, ndimage

filepath = './test_image'
for filename in os.listdir(filepath):
	img = cv2.imread('./test_image/%s' % filename)
	gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
	edges = cv2.Canny(gray,50,150,apertureSize=3
	# 霍夫变换
	lines = cv2.HoughLines(edges,1,np.pi/180,0)
	for rho,theta in lines[0]:
	    a = np.cos(theta)
	    b = np.sin(theta)
	    x0 = a * rho
	    y0 = b * rho
	    x1 = int(x0 + 1000 * (-b))
	    y1 = int(y0 + 1000 * (a))
	    x2 = int(x0 - 1000 * (-b))
	    y2 = int(y0 - 1000 * (a))
	if x1 == x2 or y1 == y2:
		continue
	t = float(y2-y1)/(x2-x1)
	rotate_angle = math.degrees(math.atan(t))
	if rotate_angle > 45:
		rotate_angle = -90 + rotate_angle
	elif rotate_angle < -45:
		rotate_angle = 90 + rotate_angle
	rotate_img = ndimage.rotate(img, rotate_angle)
	misc.imsave('./test_image/%s' % filename, rotate_img)

2.3.2 Radon 变换

Radon 变换以线积分的形式将图像投影到 ($s,\theta$) 空间。
与霍夫的区别：霍夫变换是直线参数变换的离散形式，Radon 变换则是直线参数变换的连续形式。

from scipy import ndimage
import numpy as np
import matplotlib.pyplot as plt
import imageio
from cv2 import cv2

def DiscreteRadonTransform(image, steps):
    channels = len(image[0])
    res = np.zeros((channels, channels), dtype='float64')
    for s in range(steps):
        rotation = ndimage.rotate(image, -s*180/steps, reshape=False).astype('float64')
        res[:,s] = sum(rotation)
    return res

# 读取原始图片
# image = cv2.imread("test.png", cv2.IMREAD_GRAYSCALE)
image = imageio.imread('test.jpg').astype(np.float64)
radon = DiscreteRadonTransform(image, len(image[0]))
print(radon.shape)

# 绘制原始图像和对应的 sinogram 图
plt.subplot(1, 2, 1)
plt.imshow(image, cmap='gray')
plt.subplot(1, 2, 2)
plt.imshow(radon, cmap='gray')
plt.show()

2.3.3 基于 PCA 的方法

PCA 算法需要计算对倾斜角度的分布具有最大影响的特征向量，即分布的主分量，因此首先需要将黑色像素点（即前景）映射为二维向量，使每个像素点与相同坐标的二维向量相匹配，并对每个维度减去其对应强度的均值，然后计算向量几何的协方差矩阵。