【信息流推荐论文大赏】Predicting Clicks: Estimating the Click-Through Rate for New Ads

太长不看版

Predicting Clicks: Estimating the Click-Through Rate for New Ads

论文主要思想：提出了一种预测新广告CTR的办法。

论文使用方法：提出了新的特征，使用逻辑回归 (logistic regression) 模型训练，使用模型预测CTR的 KL散度和均方差(MSE)来验证实验效果。

上述新的特征包括以下四个方面：

• CTR相关特征：
  • Term CTR：包含相同关键词的其他广告的CTR
  • Related Term CTR：包含相近关键词的其他广告的CTR
• 新广告本身特征
  • Appeareanc：广告本身是否美观
  • Attention Capture：广告是否有吸引力
  • Reputation：广告主的知名度
  • Landing Page Quality：登陆页的质量（我理解为广告引流页的质量）
  • Relevance：广告和用户检索词 (search query)的相关性
• 广告指向的明确性：
  • 作者认为指向越明确的广告CTR越高
• 外部特征：
  • 关键词在网络上的词频
  • 关键词在搜索引擎上的词频

Motivation

为什么要预测广告CTR?

因为广告主爸爸给钱。例如谷歌雅虎等广告主爸爸会按照点击结算方式(cost-per-click CPC)给钱，即用户每点一次广告，爸爸就要给一次钱。

卑微的广告展示方怎么才能挣到更多钱呢，他们可以用这个公式计算收入的期望值：
$$E_{ad}[revenue]=p_{ad}(click)\ast CP{C}_{ad}$$
其中$CP{C}_{ad}$是广告爸爸对一次点击的出价，$p_{ad}(click)$是对该条广告的点击率预测(CTR)。出价是爸爸定的，但是把CTR高的广告往前放，卑微的广告展示方就可以挣到更多钱。

这里论文作者做了一个简单的解释，在广告展示界面上，排在越靠前的广告被用户注意到的可能性越大(这也导致CTR越大)。因此，在决定广告出现顺序的时候，需要精确预估每条广告的CTR，然后把CTR高的排前面。

在预估每条广告的CTR时，作者先排除了广告出现位置的影响，否则就会死锁：广告CTR越高越往前放，越往前放进而导致CTR越高，就不好计算了。

为什么要预测新广告的CTR？

因为广告主爸爸每天发来的新广告特别多，由于缺少历史点击数据，无法准确预估其CTR，卑微的广告展示方需要尽快确定新广告质量，以决定投放顺序，挣更多钱。所以作者针对这个问题，提出了一系列的新特征来拟合新广告的质量。

广告搜索框架

广告的点击率(CTR)由两个因素决定：

• 用户看到它的可能性：由广告出现的位置(pos)决定
• 用户看到它之后点击它的可能性：由它本身质量决定

因此，广告的点击率可以公式化为：
$$p(click|ad,pos)=p(click|ad,pos,seen)\ast p(seen|ad,pos)$$
为此，论文作者做了简化假设，假设广告被用户看到的概率只与出现位置有关(与广告本身质量无关)；用户看见广告后，点击它的概率只与广告质量有关(与广告出现位置无关)。这里有点绕口，其实就是假定了上述两个因素互相独立。于是，公式可以简化为：
$$p(click|ad,pos)=p(click|ad,seen)\ast p(seen|pos)$$
本文中作者研究的CTR是$p(click|ad,seen)$，即用户看到广告后点击它的概率。因为广告在不同位置被看到的概率可以假定为一条固定的曲线，对任何广告，给定位置就有对应的“被看见概率”，所以这不是本文讨论的范围。

作者提出来的新特征

1. Estimating Term CTR

预测一条新广告的CTR时，作者首先使用了和新广告有相同或相近关键词的其他广告的CTR来构建特征，辅助预测。

1.1 Term CTR

含义：和当前广告含有相同关键词的广告的平均CTR。

该特征的计算公式为：
$$f_0(ad)=\frac{\alpha \overline{CTR}+N(a{d}_{term})\ast CTR(a{d}_{term})}{\alpha +N(a{d}_{term})}$$
其中：

• $\overline{CTR}$ 是训练集中所有广告的CTR的平均值(先验特征)
• $\alpha$ 是先验特征的比例
  这两项的作用是针对新广告中有未出现过关键词或者低频关键词。
• $N(a{d}_{term})$ 是包含相同关键词的其他广告的数量(忽略词序)，
• $CTR(a{d}_{term})$ 是包含相同关键词的其他广告的平均CTR

本实验中$\alpha$设置为1，并且作者发现实验结果对$\alpha$取值不敏感。

实验结果：

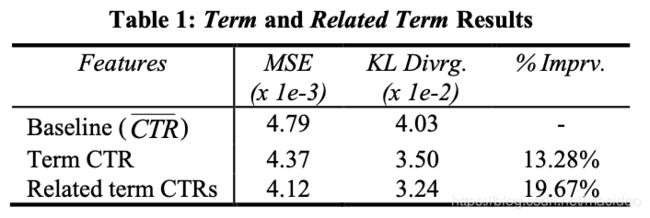
第一行是baseline，即只使用了$\overline{CTR}$ 这个特征。第二行是使用了Term CTR的实验结果，性能有13.28%的提升。

1.2. Related Term CTR

含义：与当前广告有相关关键词的广告的平均CTR。

相关是指：假设$R_{mn}(t)$是一组广告的关键词，当从t中删除m个关键词，从新广告中删除n个关键词后，他们会有相同关键词。 可以理解为，将当前广告的关键词经过一定的增删编辑操作后，可以得到的关键词，就是相关关键词。
$$R_{mn}(t)=\{\begin{array}{lr}|a{d}_{item}\cap t|>0and& \\ |t-a{d}_{item}|=mand& \\ |a{d}_{item}-t|=n& \end{array}$$
例如，如果$t$是“red shoes”，那么对于新广告中的关键词“buy red shoes”就是$R_{01}$，关键词“shoes”就是$R_{10}$，关键词“blue shoes”就是$R_{11}$。

所以，该特征的计算公式为：
$$CT{R}_{mn}(term)=\frac{1}{|R_{mn(term)}|}\sum _{x\in R_{mn(term)}}CT{R}_x$$
其中CTR_{mn}(term)和上一个特征一样要做平滑处理。

另外，作者还把相关广告的数量也作为一个特征：
$$v_{mn}(term)=｜R_{mn}｜$$

实验结果

参考table1的第三行，相比于baseline有19.67%的提升。

2. Estimating AD Quality

由于广告的CTR的变化范围很大，方差特别大，所以仅仅用CTR这个特征是不够准确的。作者统计了一些常用关键词的CTR变化范围，如下图：

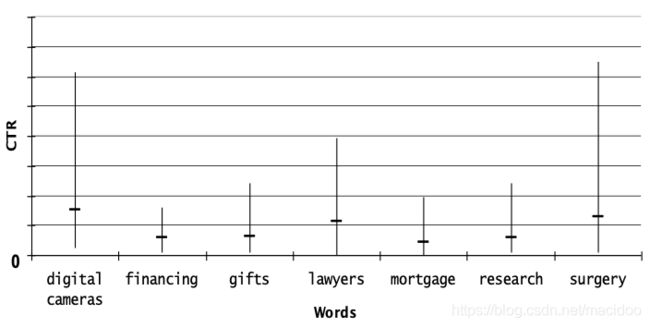
例如，对于surgery这个关键词，其最大的CTR是其平均CTR的5倍多。因此，作者还加入了广告本身质量作为其特征。

2.1. Appearance
定义：广告的外观是否符合美学。
例如，广告的标题和内容包含多少单词，广告的资本化程度好不好，是否有太多标点符号，长单词多还是短单词多？

2.2. Attention Capture
定义：广告本身是否有吸引力。
例如，广告的标题和内容里是否有“购买”、“加入”、“订阅”等关键词，是否提供了数量、价格、折扣等数字信息？

2.3. Reputation
定义：广告主的知名度
例如，显示的URL是否以.com、.net、.edu等结尾，URL被分成了多少段 (book.com就比book.something.com要好) ，是否包含破折号和数字？因为短的域名往往更贵，所以域名越好，广告主的实力越强，其广告质量也相对更好。另外，用户也会对自己更熟悉的域名更感兴趣。

2.4. Landing page quality
定义：登陆页的质量。
例如，登陆页使用了flash吗，符合W3C吗，页面中哪部分被图片遮住了，是否使用了样式表等？虽然登陆页是用户点击进去之后才能看到，但是广告往往会把用户引导到用户熟悉的登陆页上，反过来想，登陆页的质量也能反应用户是否点击该广告的概率。

2.5. Relevance
定义：广告和用户检索词汇的相关度。
例如，关键词是否准确的出现在标题中，关键词的子集是否出现在标题或者广告体中？

作者针对以上5个方面定义了81个新特征，并且添加了一元特征(unigram feature)，例如作者统计了出现在训练集中最频繁的10000个关键词，如果待测广告中包含这些关键词，该特征就取值为1，否则取值0。这些一元特征的作用是捕捉一些没有被注意到的关键词，这些词可以增加我们对广告特征的捕捉。

实验结果

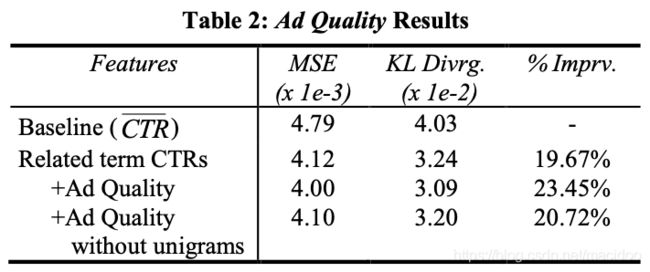
作者发现，在不使用广告词频的一元特征，仅使用广告本身质量特征，相对于baseline有20.72%的提升(图最后一行)，也就是相对于related term ctr只有1%的提升；如果加入广告词频的一元特征，相对于baseline有23.45%的提升(图倒数第二行)。

作者说这一点令他们很震惊。毕竟他们本以为一些手工定义的广告质量特征（前面说到的81个特征）会有很好的效果，可惜并不是。反而是一元特征比较有用。这里其实引发了我的一些思考，写在了文章结尾。

3. Measuring Order Specificity

作者认为指向性明确的 (即广告目标群体与广告的关键词更接近) 广告会有更高的CTR。故作者将关键词分成了74类，然后计算广告中的关键词与这74类的熵，用以表征广告指向性是否明确，并作为一个特征进行计算。

此外，作者还将广告订单中不重复的单词数量作为特征，与上述的指向性熵特征一起送入模型进行训练。

实验结果：

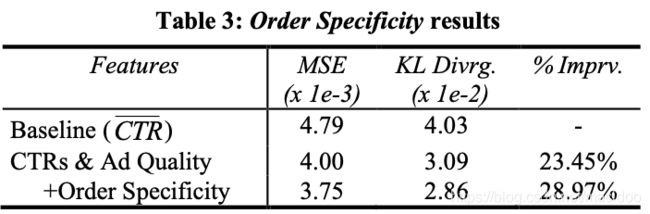
作者发现，加入这两个特征后，模型的准确率提升到了28.97%，说明这两个特征效果明显。作者为了验证这两个特征是否都有正向收益，他还尝试了只使用广告指向性特征进行训练，发现模型有26.37%的提升。而同时使用广告指向性特征和不重复单词数量特征，模型有28.97%的提升，说明这两个特征都带来了正向收益。

4. External Sources Of Data

定义：广告中关键词在Web中出现的频率和在用户近三个月中在搜索引擎中搜索的频率。

作者认为，不仅可以用广告本身的特征，还可以使用一些外部特征，即广告中关键词在Web和搜索引擎中的出现频率。因为如果广告中包含的关键词是人们经常搜索的，说明该广告有更大几率会吸引人们点击它。

对于广告中关键词在Web中出现的频率，作者使用了一个巧妙的统计方法。作者通过统计在搜索引擎中搜索该关键词，并统计包含该关键词的网页页面数，并用这个数量代表关键词出现的频率。

对于关键词在用户搜索引擎中的出现的频率，作者使用了用户最近三个月在搜索引擎中的历史记录，并统计广告中关键词在用户历史记录中的出现频率。

另外，作者对上述两个频率特征进行了分桶处理，每个特征分别分了20个桶。
实验结果

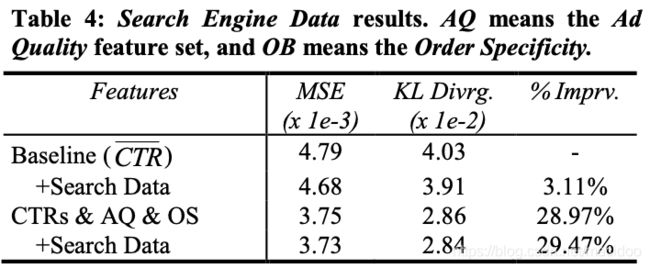
作者发现，这两个特征能在baseline的基础上带来3.11%的正向收益，但是与前面的特征结合起来后，却只有0.5%的额外收益，这说明此类特征与前面提出来的特征有较大的重合度。

数据集

本论文使用了微软公司的搜索引擎上的广告信息，每个广告都包含了以下几个方面：

• Landing page：登陆页
• Bid term：关键词
• Title：广告的标题
• Body：广告的内容
• Display URL：广告的超链接
• Clicks：自投放以来广告被点击的数量
• Views：自投放以来广告被看到的数量

整个数据集包含了超过10000个广告主爸爸，上百万条广告和50万个关键词。

由于本文研究的是新广告的CTR，即我们不知道任何关于新广告的信息，也不知道该广告主爸爸的任何信息以及他原来投放广告的信息。故作者按照广告主来划分数据集，把属于同一个广告主的广告放到一起。然后随机抽取70%的广告作为训练集，10%作为验证集，20%作为测试集。

为了实验的准确性，作者还过滤掉了浏览量少于100的广告，因为这些广告计算出来的CTR是不置信的。

模型

作者选用了逻辑回归模型，因为它非常适合预测概率，总能得到0-1之间的概率结果：
$$CTR=\frac{1}{1+e^{-Z}},Z=\sum _i{w}_i{f}_i(ad)$$
其中$f_i(ad)$是广告中第$i$个特征的值，$w_i$是相应的权重矩阵。作者使用的是交叉熵损失函数，和一个均值为0，方差为0.1的高斯权重先验(方差是通过多组实验选了个最好的值)。同时，作者还加了一个始终为1的偏置(常规操作)。

此外，作者还做了一系列的数据预处理：

• 增加了一个衍生特征$log(f_1+1)$和${f_1}^2$：目的是防止有些特征最小值为0。
• 特征数据做标准化：目的是防止离群数据的影响(使用的是训练集上的均值和方差)
• 超过标准差5倍的数据做截断：超出5倍的数据按照5倍来计算，防止特征数据的长尾效应

自己的一点思考

个人觉得本文让人比较有收获的点是：

• 构建新广告的特征考虑较为全面，不仅考虑了广告本身的吸引力，而且考虑了一些外部条件对广告的影响。
• 分析实验很“控制变量”，对于每一类新特征作者都用单独的实验验证其了有效性，并且分析了他们之间可能存在的overlap(覆盖)的情况
• 现在信息流推荐大家其实比的就是特征工程，谁的特征做得好，效果往往就会更显著。在本文中作者发现，其实一些统计特征的效果比手工特征来的更有效。手工特征往往加入了太多工程师自身对业务的理解，而统计数据才是最贴近用户行为的。