datawhale_pandas_task01
Python 基础
1. 列表推导式与条件赋值
L = []
def my_func(x):
return 2*x
for i in range(5):
L.append(my_func(i))
L
[0, 2, 4, 6, 8]
列表表达式 [映射函数 for i in 迭代的对象]
[my_func(i) for i in range(5)]
[0, 2, 4, 6, 8]
[m+'_'+n for m in ['a', 'b'] for n in ['c', 'd']]
['a_c', 'a_d', 'b_c', 'b_d']
条件赋值value = a if condition else b
value = 'cat' if 2>1 else 'dog'
value
'cat'
L = [i for i in range(1, 8)]
L
[1, 2, 3, 4, 5, 6, 7]
[num if num<=5 else 5 for num in L]
[1, 2, 3, 4, 5, 5, 5]
2. 匿名函数与map方法
my_func = lambda x: 2*x
my_func(3)
6
multi_para_func = lambda a, b: a+b
multi_para_func(3, 4)
7
[(lambda x: 2*x)(i) for i in range(5)]
[0, 2, 4, 6, 8]
它返回的是一个 map 对象，需要通过 list 转为列表
[map(lambda x: 2*x, range(5))]
[list(map(lambda x: 2*x, range(5)))
[0, 2, 4, 6, 8]
list(map(lambda x, y: str(x)+'_'+y, range(5), list('abcde')))
['0_a', '1_b', '2_c', '3_d', '4_e']
3. zip对象与enumerate方法
zip函数能够把多个可迭代对象打包成一个元组构成的可迭代对象，它返回了一个 zip 对象，通过 tuple, list 可以得到相应的打包结果：
L1, L2, L3 = list('abc'), list('def'), list('hij')
list(zip(L1, L2, L3))
[('a', 'd', 'h'), ('b', 'e', 'i'), ('c', 'f', 'j')]
tuple(zip(L1, L2, L3))
(('a', 'd', 'h'), ('b', 'e', 'i'), ('c', 'f', 'j'))
for i, j, k in zip(L1, L2, L3):
print(i, j, k)
a d h
b e i
c f j
enumerate 是一种特殊的打包，它可以在迭代时绑定迭代元素的遍历序号
for i, char in enumerate('abcd'):
print(i, char)
0 a
1 b
2 c
3 d
用 zip 对象也能够简单地实现这个功能：
arr = list('abcd')
for idx, char in zip(range(len(arr)), arr):
print(idx, char)
0 a
1 b
2 c
3 d
对两个列表建立字典映射
dict(zip(L1, L2))
{'a': 'd', 'b': 'e', 'c': 'f'}
Python 也提供了 * 操作符和 zip 联合使用来进行解压操作
zipped = list(zip(L1, L2, L3))
zipped
[('a', 'd', 'h'), ('b', 'e', 'i'), ('c', 'f', 'j')]
list(zip(*zipped))
[('a', 'b', 'c'), ('d', 'e', 'f'), ('h', 'i', 'j')]
Numpy基础
1. np数组的构造
通过array构造
特殊 ndarray 生成方法
等差序列 np.linspace, np.arange
- linspace(起始，终止（包含），样本个数)
- arange(起始，终止（不包含），步长)
特殊序列 np.zeros, np.eye, np.full
-
全0矩阵
-
单位矩阵
-
填充给定数值矩阵
随机矩阵 np.random
- 0-1均匀分布的随机数组
np.random.rand(size)
服从区间 到 上的均匀分布可以如下生成
- (0,) 的标准正态分布
np.random.randn(size)
服从方差为 2 均值为 的一元正态分布
- 最小值最大值（不包含）的随机整数
np.random.randint(low, high, size)
- 从给定列表中，以一定概率和方式随机抽样
np.random.choice(array, size, replace=False, p=probability)
- 打散原列表（返回元素个数于原列表相同）
np.random.permutation(array)
随机种子 - 固定随机数的输出结果
2. np数组的变形与合并
转置： T
合并操作： r_, c_
- 上下合并
r_ - 左右合并
c_
一维数组和二维数组进行合并时，应当把其视作列向量，在长度匹配的情况下只能够使用左右合并的c_操作
维度变换： reshape
reshape – 把原数组按照新的维度重新排列。在使用时有两种模式:
- C 模式
target.reshape(shape, order='C')- 逐行的顺序进行填充读取 - F 模式，
target.reshape(shape, order='F')- 逐列的顺序进行填充读取
由于被调用数组的大小是确定的， reshape 允许有一个维度存在空缺，此时只需填充-1（numpy会帮忙自动补全）
3. np数组的切片与索引
slice 类型的 start:end:step 切片
数组的切片模式支持使用 slice 类型的 start:end:step 切片，还可以直接传入列表指定某个维度的索引进行切片
np.ix_
此外，还可以利用 np.ix_ 在对应的维度上使用布尔索引，但此时不能使用 slice 切片
其中第一个
[True, False, True]是取target中的 index=0和 index=2 行
第二个[True, False, True]是取target中的 index=0和 index=2 列
True (取) False (不取) True (取)
True (取) [0, 1, 2],
False (不取) [3, 4, 5],
True (取) [6, 7, 8]
取target中的第[1,2]行，第0，2列
4. 常用函数
where
条件函数，指定满足条件与不满足条件位置对应的填充值
nonzero, argmax, argmin 返回索引
nonzero返回非零数的索引argmax返回最大数的索引argmin返回最小数的索引
含有缺失值的数组
any, all
any指当序列至少 存在一个 True 或非零元素时返回 True ，否则返回 Falseall指当序列元素 全为 True 或非零元素时返回 True ，否则返回 False
cumprod, cumsum, diff
- cumprod 累乘函数，返回同长度的数组
- cumsum 累加函数，返回同长度的数组
- diff 表示和前一个元素做差，返回长度是原数组减1
统计函数
常用的统计函数包括 max, min, mean, median, std, var, sum, quantile ，其中分位数计算是全局方法，因此不能通过 array.quantile 的方法调用
对于含有缺失值的数组，它们返回的结果也是缺失值，如果需要略过缺失值，必须使用 nan* 类型的函数，上述的几个统计函数都有对应的 nan* 函数
对于协方差和相关系数分别可以利用cov,corrcoef如下计算
5. 广播机制
标量和数组的操作
二维数组之间的操作
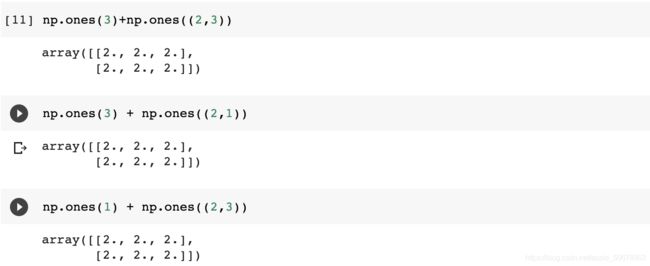
当两个数组维度完全一致时，使用对应元素的操作，否则会报错，除非其中的某个数组的维度是 ×1 或者 1× ，那么会扩充其具有 1 的维度为另一个数组对应维度的大小。
例如， 1×2 数组和 3×2 数组做逐元素运算时会把第一个数组扩充为 3×2 ，扩充时的对应数值进行赋值。但是，需要注意的是，如果第一个数组的维度是 1×3 ，那么由于在第二维上的大小不匹配且不为 1 ，此时报错。
一维数组与二维数组的操作
当一维数组 与二维数组 , 操作时，等价于把一维数组视作 1, 的二维数组，使用的广播法则与【b】中一致，当 != 且 , 都不是 1 时报错。
6. 向量与矩阵的计算
向量内积： dot
向量范数和矩阵范数： np.linalg.norm
return one of eight different matrix norms, or one of an infinite number of vector norms (described below), depending on the value of the
ordparameter.
【向量范数】
对于向量 x = [ x 1 , x 2 , . . . , x m ] x = [x_1, x_2, ... , x_m] x=[x1,x2,...,xm], 常用的范数包括
- 1-范数
- 即向量元素绝对值之和，x 到零点的曼哈顿距离
- 2-范数
- 2-范数也称为Euclid范数（欧几里得范数，常用计算向量长度），即向量元素绝对值的平方和再开方，表示x到零点的欧式距离
- p-范数
- 向量元素绝对值的p次方和的1/p次幂，表示x到零点的p阶闵氏距离。
- ∞ \infty ∞ -范数
- 当p趋向于正无穷时，即所有向量元素绝对值中的最大值
- − ∞ -\infty −∞ -范数
- 当p趋向于负无穷时，即所有向量元素绝对值中的最小值
- 0-范数
- 当p趋于零，可以证明这时候的极限恰好是向量非零元素的个数。
【矩阵范数】
对于矩阵
- 1-范数
- 列和范数，即所有矩阵列向量绝对值之和的最大值
- 2-范数
- ∞ \infty ∞ -范数
- 行和范数，即所有矩阵行向量绝对值之和的最大值
- F -范数
- Frobenius范数，即矩阵元素绝对值的平方和再开平方
| ord | norm foR matrices | norm for vectors |
|---|---|---|
| None | Frobenius norm | 2-norm |
| ‘fro’ | Frobenius norm | - |
| ‘nuc’ | nuclear norm | - |
| inf | max(sum(abs(x), axis=1)) | max(abs(x)) |
| -inf | min(sum(abs(x), axis=1)) | min(abs(x)) |
| 0 | - | sum(x != 0) |
| 1 | max(sum(abs(x), axis=0)) | as below |
| -1 | min(sum(abs(x), axis=0)) | as below |
| 2 | 2-norm (largest sing. value) | as below |
| -2 | smallest singular value | as below |
| other | - | sum(abs(x)**ord)**(1./ord) |
矩阵乘法： @
[[0 1] * [[-4 -3] = [[0*-4+1*-2 0*-3+1*-1] = [[-2 -1]
[2 3]] [-2 -1]] [2*-4+3*-2 2*-3+3*-1]] [-14 -9]
练习
Ex1：利用列表推导式写矩阵乘法
一般的矩阵乘法根据公式，可以由三重循环写出：
In [138]: M1 = np.random.rand(2,3)
In [139]: M2 = np.random.rand(3,4)
In [140]: res = np.empty((M1.shape[0],M2.shape[1]))
In [141]: for i in range(M1.shape[0]):
.....: for j in range(M2.shape[1]):
.....: item = 0
.....: for k in range(M1.shape[1]):
.....: item += M1[i][k] * M2[k][j]
.....: res[i][j] = item
.....:
In [142]: ((M1@M2 - res) < 1e-15).all() # 排除数值误差
Out[142]: True
请将其改写为列表推导式的形式。
思路：
- 2x3 M_1矩阵 * 3x4 M_2矩阵 = 2x4 M_final矩阵
- M_final 的第一个num（最左上角）等于 M_1的第一行的每个数乘以 M_2的第一列的每个数 的和
sum(M_1[0][0]*M_2[0][0], M_1[0][1]*M_2[1][0], M_1[0][2]*M_2[2][0])- 在这个sum里，在变的是M_1的第二个index和M_2的第一个index，且都是从0到2，我们可以用 k for k in range(M_1.shape[1])，上面sum就变成了
sum(M_1[0][k]*M_2[k][0], M_1[0][k]*M_2[k][0], M_1[0][k]*M_2[k][0])- M_final的第一行 其实是M_1的第一行和M_2的每一列的各自乘积和，aka在M_1的第一行的时候，我们应该循环一遍M_2的每个列，让他们进行上面的sum操作
- 最外圈我们要把M_1的每一行循环一遍
Ex2：更新矩阵
思路
- 因为matrix B的shape会和matrix A的shape是一样的，所以先创建一个和A shape一样的全是1的矩阵
- 然后按照公示，两个for loop + 一个对A每行的倒数求和loop就ok了
Ex3：卡方统计量
Ex4：改进矩阵计算的性能
Ex5：连续整数的最大长度
输入一个整数的 Numpy 数组，返回其中递增连续整数子数组的最大长度。例如，输入 [1,2,5,6,7]，[5,6,7]为具有最大长度的递增连续整数子数组，因此输出3；输入[3,2,1,2,3,4,6]，[1,2,3,4]为具有最大长度的递增连续整数子数组，因此输出4。请充分利用 Numpy 的内置函数完成。（提示：考虑使用 nonzero, diff 函数）
思路
- 每个num（除了第一个）和他们前面一个num的差值
- 找到最长的连续11111111得到长度再加1
啊好难