Boggle
1. 问题描述
princeton_algs4第四周的编程作业Boggle,一个拼字游戏。将棋盘上的字母按照限定的顺序连接,如果得到给定字典中出现的单词,则记分。
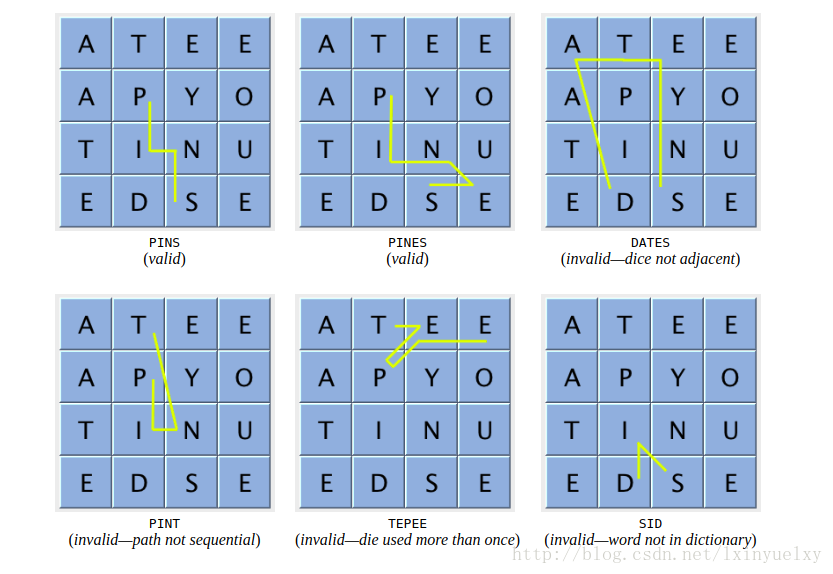
一个合法的单词必须满足以下条件:
- 一个字母只能够与它的上、下、左、右、左上、右上、左下、右下8个方向上的字母相连。
- 单词中同一个位置的字母只能出现一次。
- 单词至少有三个字母。
- 单词必须存在于给定的字典中。
我们要完成的任务就是:已知一个字典和一个棋盘(棋盘上每个位置的字母可以得到),找出该棋盘上的字母可以组成的所有合法单词。
2. 解决思路
2.1 对棋盘建模
我们考虑如何在棋盘上搜索单词。既然每个单词是沿着棋盘上的字母与其临接的字母一个一个串起来的,那么我们可以把棋盘看成图,棋盘上各位置的字母可以看成图中的结点,从一个字母与其能达到的另一个字母之间建立一条边,假设一个4*4大小的棋盘可以构成如下的无向图。

其实这里我们不用真正构建一幅图,我们的主要目的是以某个字母为起点时,要很方便的得到它所有的临接点来组成单词,因此我们真正需要的是一个临接表。这里我用了一个数组来存储Bag类型的数据,一个Bag存储的是一个字母的所有临接字母。
rows = board.rows();
cols = board.cols();
adj = (Bag[]) new Bag[rows*cols];
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
int v = i*cols + j;
adj[v] = new Bag();
if (checkWIsValid(i-1, j)) adj[v].add((i-1) * cols + j);
if (checkWIsValid(i+1, j)) adj[v].add((i+1) * cols + j);
if (checkWIsValid(i, j+1)) adj[v].add(i * cols + j+1);
if (checkWIsValid(i, j-1)) adj[v].add(i * cols + j-1);
if (checkWIsValid(i+1, j-1)) adj[v].add((i+1) * cols + j-1);
if (checkWIsValid(i+1, j+1)) adj[v].add((i+1) * cols + j+1);
if (checkWIsValid(i-1, j-1)) adj[v].add((i-1) * cols + j-1);
if (checkWIsValid(i-1, j+1)) adj[v].add((i-1) * cols + j+1);
}
} 2.2 改造深度优先搜索
接下来我们可以使用深度优先的方法在图中搜索所有的合法单词。首先判断是否出现了合法单词:当前字符串长度大于2,并且存在于与字典中。如果是合法单词,就记录下来并且继续搜索。这里有一个限制条件要注意:就是同一个位置的字母不能两次出现在得到的字符串中。如果我们使用一般DFS中用一个boolean型数组marked[]来标记当前所遍历到的结点时就会出现一个问题:原本marked标记的是所有遍历过的结点,如果某个结点已经遍历过了,则下次遍历到它时就会跳过。而我们这里的需求是正在遍历的结点们中不能重复出现同一个位置的结点。举个例子:假如说 PINES 和 PIDS 都是合法的单词。我们沿着P—-I—-N—-E—-S一路遍历下来,得到了PINES这个合法单词,这些正在被遍历的点都应该被标记,当我们继续遍历到P——I——D时,之前遍历过的N,E,S结点这时候应该被取消标记,不然我们就遍历不到S结点,就无法找出合法的单词PIDS了。改造后的marked[]与之前的区别就是,之前marked就是负责把所有遍历过的点标记出来,而现在我们只标记所有存在于当前搜索出的路径上的结点,一旦某个节点不在当前遍历的路径上时,则立即取消标记。于是我的做法是除了之前的数组marked[],新加了一个数据Stack用来记录当前路径遍历到的结点。一旦完成某个结点的遍历,则立刻从栈顶弹出该结点,并取消相应标记。
private void searchValidWords(int v, Node x, String str, Stack visitingDices) {
if (str.length() > 2 && x != null && x.val == 1) {
validWords.add(str);
}
for (int w : adj[v]) {
char c = getLetterOnBoard(w);
if (!marked[w] && x != null && x.next[c -'A'] != null) {
visitingDices.push(w);
marked[w] = true;
if (c == 'Q') {
searchValidWords(w, x.next['Q'-'A'].next['U' - 'A'], str+"QU", visitingDices);
}
else {
searchValidWords(w, x.next[c -'A'], str+c, visitingDices);
}
int index = visitingDices.pop();
marked[index] = false;
}
}
} 2.3 对字典建模
最后还有一个大问题要解决:如何快速地在字典中查找一个单词是否存在与该字典中。由于这周主要讲的数据结构是前缀树Trie,所以毫无疑问,我们应该将字典存储在Trie中。其实也可以这样理解:我们用给定的字典构建出一棵前缀树(也叫字典树)后,棋盘上以某个字母为起点用DFS遍历到的字母顺序,就是在字典树中前进的方向,如果前进到某个结点为空,则说明在字典中不存在以DFS遍历到的字符串为前缀的单词,因此对于棋盘来说也就没有必要在当前结点继续用DFS搜索下去了。
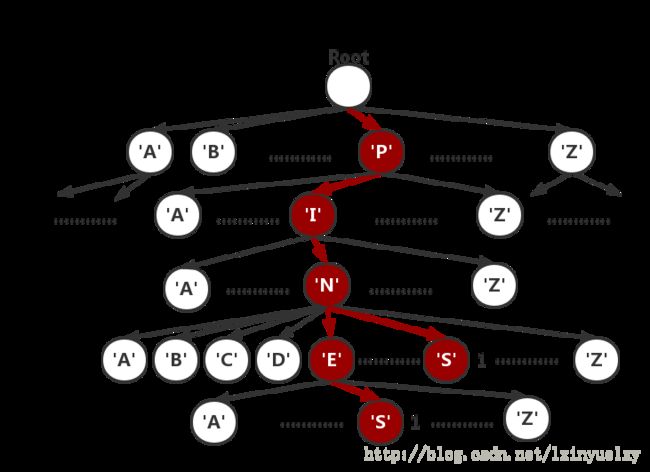
道理大概就是这样。我最开始直接调用了algs4包中的APITrieST.java(R-way tries)和TST.java(ternary search tries),不幸的是都挂掉了,这次的作业对时间复杂度卡的很严。于是乎发现有一个地方比较耗时:原先我在每次用DFS搜索时,首先判断字典中是否出现了合法单词时都是直接调用keysWithPrefix函数并且判断它的value不为空,然而这个操作每次都从树根开始查找,这就好比你第一遍DFS时得到字符串"P",然后在字典树中从Root开始查找,存在键值为P的结点,好的继续第二遍DFS得到字符串"PI",字典树又从Root开始找起,先找到P,再从P的子结点中找到键值为I的子结点。到第三遍在字典树中查找时,继续从Root查找,因此这个步骤存在很多冗余操作。解决方法是DFS时,记录下当前遍历到的树中的结点。所以你可以看到在上面查找合法单词的函数中,有一个参数Node x 就是在记录字典树中当前遍历到的结点。
字典树的构建代码如下:
public BoggleSolver(String[] dictionary) {
root = new Node();
for (int i = 0; i < dictionary.length; i++) {
put(dictionary[i]);
}
}
private static class Node {
private int val = 0;
private Node[] next = new Node[26];
}
private int get(String key) {
Node x = get(root, key, 0);
if (x == null) return 0;
return x.val;
}
private Node get(Node x, String key, int d) {
if (x == null) return null;
if (d == key.length()) return x;
int c = key.charAt(d) - 'A';
return get(x.next[c], key, d+1);
}
private void put(String key) {
root = put(root, key, 0);
}
private Node put(Node x, String key, int d) {
if (x == null) x = new Node();
if (d == key.length()) {
x.val = 1;
return x;
}
int c = key.charAt(d) - 'A';
x.next[c] = put(x.next[c], key, d+1);
return x;
}3. 代码
查看完整代码戳这里