Tensorflow非线性回归的应用

Tensorflow非线性回归的应用

线性回归训练的是k、d,非线性回归用的是神经网络来训练权值w，tensorflow 2.0版本有很多坑要注意,完整代码写在最后

首先给出一个非线性的关系$y=x^2$，再加上一个正态分布的噪声，通过神经网络训练得到输入输出关系

• tf.compat.v1.disable_eager_execution()是由于tensorflow 2.x版本和1.x版本不兼容加上的

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
tf.compat.v1.disable_eager_execution()
# np.linspace(-0.5,0.5,200)是在-0.5到0.5之间生成200个点 [:,np.newaxis]是把数据变成200行1列
x_data = np.linspace(-0.5,0.5,200)[:,np.newaxis]
noise = np.random.normal(0,0.02,x_data.shape)
y_data = np.square(x_data) + noise

plt.scatter(x_data,y_data)

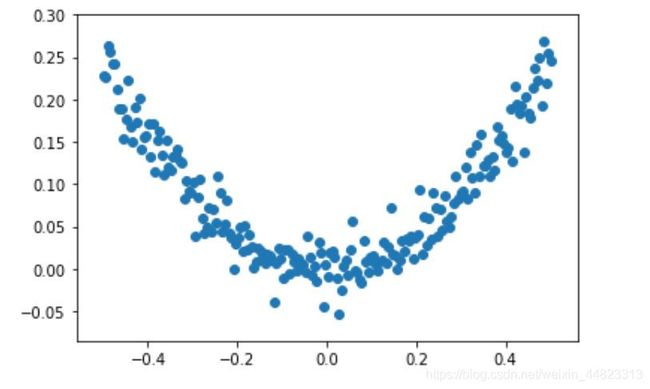
输入输出关系如上图所示，下面通过神经网络来获得训练模型
1.首先要先定义运算法则，然后在session中进行运算，x、y则是运算的输入输出数据，这里定义成n行1列的占位符，多少行没有限定，所以用None表示。
2.神经网络定义成1-20-1的结构，即隐层有20个神经元，故输入层到隐层的权重$w_1$定义为1×20,隐层到输出层权重$w_2$定义为20×1，偏置$b_1,b_2$初始值都设置为0，值得注意的是$b_1,b_2$这里都是一维的，并没有定义成array形式，定义成array做加法就可能出错，因为一维的list不区分行和列，该是行相加它就认为是行相加，该是列相加，它就认为是列相加，这里xw1_plus_b1应该是列相加。
3.激活函数用的是tanh，也可以用relu函数，但是效果就不太好，影响训练效果的几个因素有：训练次数，激活函数，神经元个数和隐层层数
4.构建代价函数(MSE,Mean Square Error)用到的函数是
loss = tf.reduce_mean(tf.square(y - L2)),用loss = tf.losses.mean_squared_error(y,L2)则会出错，因为在tensorflow 1.x中这两个运算结果是一样的，而在2.x版本中结果则不一样，案例如下所示，在tf 2.0中可以用tf.compat.v1.losses.mean_squared_error(y,L2)

a = tf.constant([[4.0, 4.0, 4.0], [3.0, 3.0, 3.0], [1.0, 1.0, 1.0]])
b = tf.constant([[1.0, 1.0, 1.0], [1.0, 1.0, 1.0], [2.0, 2.0, 2.0]])
print(a)
print(b)
with tf.compat.v1.Session() as sess:
    print(sess.run(a))
    print(sess.run(b))
    print("\n")
c = tf.square(a - b)
mse1 = tf.reduce_mean(c) 
with tf.compat.v1.Session() as sess:
    #print(sess.run(c))
    print(sess.run(mse1))    
mse2 = tf.losses.mean_squared_error(a,b)
with tf.compat.v1.Session() as sess:
    print(sess.run(mse2))  

结果显示

Tensor("Const_70:0", shape=(3, 3), dtype=float32)
Tensor("Const_71:0", shape=(3, 3), dtype=float32)
[[4. 4. 4.]
 [3. 3. 3.]
 [1. 1. 1.]]
[[1. 1. 1.]
 [1. 1. 1.]
 [2. 2. 2.]]


4.6666665
[9. 4. 1.]

可以看出tf.losses.mean_squared_error(y,L2)算出来均方差的是一个列表，而loss = tf.reduce_mean(tf.square(y - L2))算出来的值正是这个列表的均值，显然我们用一个列表作为loss来作为代价函数，使其最小化，我们对这个运算的过程了解是不明朗的，但在tensorflow 1.x版本中是可以用的。

5.在训练中feed数据x_data,y_data时候要以字典形式输入，每训练150次查看一次loss的值

# 定义两个占位符
# [None,1]表示数据是n行1列的
x = tf.compat.v1.placeholder(tf.float32,[None,1])
y = tf.compat.v1.placeholder(tf.float32,[None,1])

# 定义神经网络结构 1-20-1
# 定义运算
# 权重w,偏置b1
w1 = tf.Variable(tf.random.normal([1,20]))
# 这里b1是一个一维数组shape = （20,），表示有20个元素，故下面 tf.matmul(x,w1) + b1 是可以相加的，
# 但如果b1是二维数组，表示20行1列时候，肯定就会报错，一维数组没有行和列，这里加法运算可以把b1看做1行20列进行加法
b1 = tf.Variable(tf.zeros([20]))
xw1_plus_b1 = tf.matmul(x,w1) + b1
# 激活函数用的是tanh
L1 = tf.nn.tanh(xw1_plus_b1)

w2 = tf.Variable(tf.random.normal([20,1]))
b2 = tf.Variable(tf.zeros([1]))
xw2_plus_b2 = tf.matmul(L1,w2) + b2
L2 = tf.nn.tanh(xw2_plus_b2)

# 构建代价函数
#loss = tf.losses.mean_squared_error(y,L2) 用这个做代价函数应该和下面那个是一样的，
#但在tensorflow2.0中我发现结果不一样，最后有案例
loss = tf.reduce_mean(tf.square(y - L2))

# 梯度下降法
train = tf.compat.v1.train.GradientDescentOptimizer(0.1).minimize(loss)

#创建会话
with tf.compat.v1.Session() as sess:
    # 初始化变量
    sess.run(tf.compat.v1.global_variables_initializer())
    for i in range(3000):
        sess.run(train,feed_dict = {
     x:x_data,y:y_data})
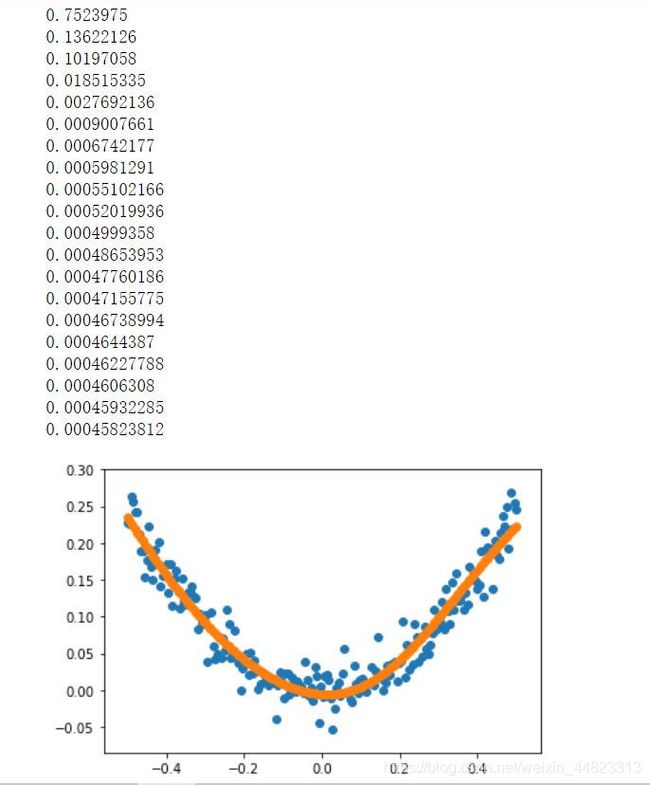
        if i%150 == 0:
            print(sess.run(loss,feed_dict = {
     x:x_data,y:y_data}))
        
    prediction_values = sess.run(L2,feed_dict = {
     x:x_data})
    plt.scatter(x_data,y_data)
    plt.scatter(x_data,prediction_values)
    plt.show()
    

训练结果

完整代码如下

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
tf.compat.v1.disable_eager_execution()
# np.linspace(-0.5,0.5,200)是在-0.5到0.5之间生成200个点 [:,np.newaxis]是把数据变成200行1列
x_data = np.linspace(-0.5,0.5,200)[:,np.newaxis]
noise = np.random.normal(0,0.02,x_data.shape)
y_data = np.square(x_data) + noise

plt.scatter(x_data,y_data)
# 定义两个占位符
# [None,1]表示数据是n行1列的
x = tf.compat.v1.placeholder(tf.float32,[None,1])
y = tf.compat.v1.placeholder(tf.float32,[None,1])

# 定义神经网络结构 1-20-1
# 定义运算
# 权重w,偏置b1
w1 = tf.Variable(tf.random.normal([1,20]))
# 这里b1是一个一维数组shape = （20,），表示有20个元素，故下面 tf.matmul(x,w1) + b1 是可以相加的，
# 但如果b1是二维数组，表示20行1列时候，肯定就会报错，一维数组没有行和列，这里加法运算可以把b1看做1行20列进行加法
b1 = tf.Variable(tf.zeros([20]))
xw1_plus_b1 = tf.matmul(x,w1) + b1
# 激活函数用的是tanh
L1 = tf.nn.tanh(xw1_plus_b1)

w2 = tf.Variable(tf.random.normal([20,1]))
b2 = tf.Variable(tf.zeros([1]))
xw2_plus_b2 = tf.matmul(L1,w2) + b2
L2 = tf.nn.tanh(xw2_plus_b2)

# 构建代价函数
#loss = tf.losses.mean_squared_error(y,L2) 用这个做代价函数应该和下面那个是一样的，
#但在tensorflow2.0中我发现结果不一样，最后有案例
loss = tf.reduce_mean(tf.square(y - L2))

# 梯度下降法
train = tf.compat.v1.train.GradientDescentOptimizer(0.1).minimize(loss)

#创建会话
with tf.compat.v1.Session() as sess:
    # 初始化变量
    sess.run(tf.compat.v1.global_variables_initializer())
    for i in range(3000):
        sess.run(train,feed_dict = {
     x:x_data,y:y_data})
        if i%150 == 0:
            print(sess.run(loss,feed_dict = {
     x:x_data,y:y_data}))
        
    prediction_values = sess.run(L2,feed_dict = {
     x:x_data})
    plt.scatter(x_data,y_data)
    plt.scatter(x_data,prediction_values)
    plt.show()