一、背景
0.0 神说,要有正态分布,于是就有了正态分布。
0.1 神看正态分布是好的,就让随机误差都随了正态分布。
0.2 正态分布的奇妙之处,就是许多看似随机事件竟然服从一个表达式就能表达的分布,如同上帝之手特意为之。
神觉得抛硬币是好的,于是定义每个抛出硬币正面记+1分,反面记-1分。创世纪从0分开始,神只抛1次硬币,有2种可能:一半的概率+1分,一半的概率-1分。此时概率分布大概是这样的:
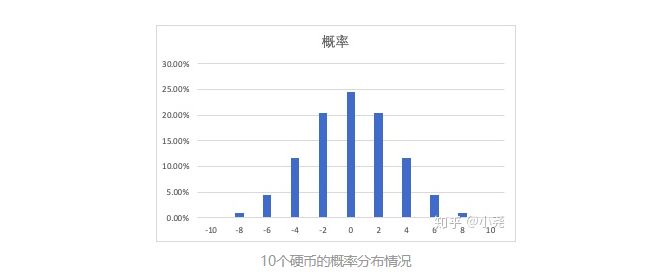
神决定扔10个硬币,此时概率分布如下:
如果画图来感受,数据分布大概如下:
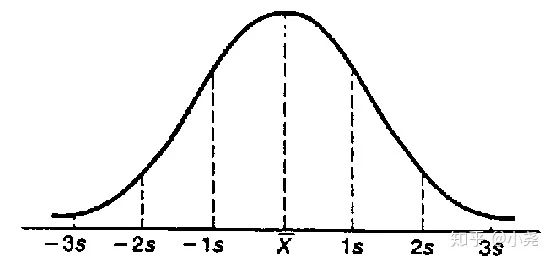
如果是100个,甚至是无穷多个呢?平均分数分布情况大概是什么样呢?画个图感受一下:
——《创世纪·数理统计·正态分布的前世今生》
开头摘自统计学中非常经典的一本书籍,由此可见正态分布是非常经典和随处可见的,为什么正态分布这么常见呢?因为通常情况下,一个事物的影响因素都是多个,好比每个人的学习成绩,受到多个因素的影响,比如:
- 本人的智商情况。
- 上课听讲的认真程度,课前的预习程度,与老师的互动程度。
- 课后是否及时复习,有没有及时温习知识点呢,有没有做好作业巩固。
每一天的因素,每天的行为,对于学生的成绩不是产生正面因素就是负面因素,这些因素对于成绩的影响不是正面就是负面的,反复累计加持就像上图的抛硬币一样,让成绩最后呈现出正态分布。数据呈现正态分布其实背后是有中心极限定理原理支持,根据中心极限定理,如果事物受到多种因素的影响,不管每个因素单独本身是什么分布,他们加总后结果的平均值就是正态分布。
二、引用
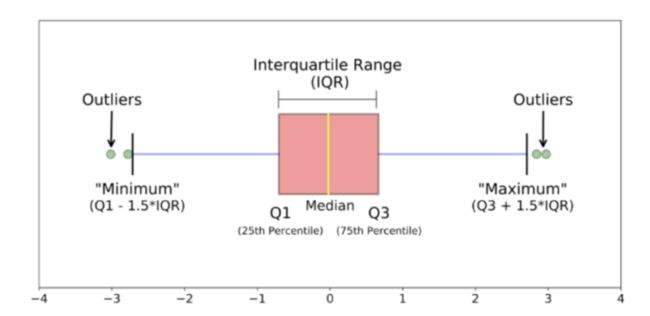
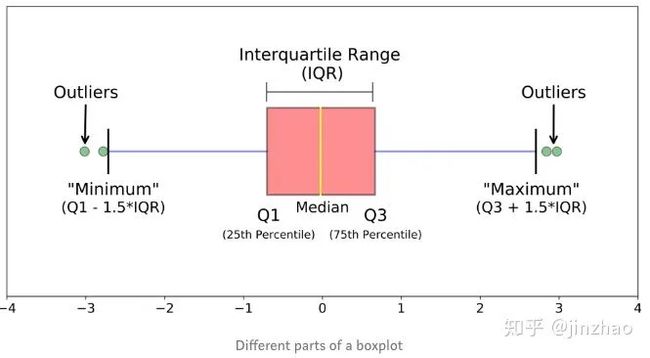
正是因为日常分析工作中数据呈现是正态分布的,处于两个极端的值往往是异常的,与我们挑选异常值天然契合。在业务方寻求一种自动监控方案的过程中,我们选择了该方案。根据数据分析工作中,结合统计学的数据阈值分布原理,通过自动划分数据级别范围,确定异常值,如下图箱线图,箱线图是一个能够通过5个数字来描述数据的分布的标准方式,这5个数字包括:最小值,第一分位,中位数,第三分位数,最大值,箱线图能够明确的展示离群点的信息,同时能够让我们了解数据是否对称,数据如何分组、数据的峰度。
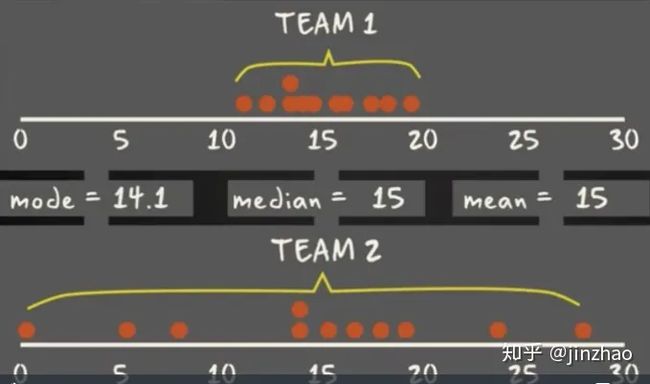
箱线图是一个能够通过5个数字来描述数据的分布的标准方式,这5个数字包括:最小值,第一分位,中位数,第三分位数,最大值,箱线图能够明确的展示离群点的信息,同时能够让我们了解数据是否对称,数据如何分组、数据的峰度,对于某些分布/数据集,会发现除了集中趋势(中位数,均值和众数)的度量之外,还需要更多信息。
(图片来源于网络)
需要有关数据变异性或分散性的信息。箱形图是一张图表,它很好地指示数据中的值如何分布,尽管与直方图或密度图相比,箱线图似乎是原始的,但它们具有占用较少空间的优势,这在比较许多组或数据集之间的分布时非常有用。——适用于大批量的数据波动监控。
(图片来源于网络)
箱线图是一种基于五位数摘要(“最小”,第一四分位数(Q1),中位数,第三四分位数(Q3)和“最大”)显示数据分布的标准化方法。
- 中位数(Q2 / 50th百分位数):数据集的中间值;
- 第一个四分位数(Q1 / 25百分位数):最小数(不是“最小值”)和数据集的中位数之间的中间数;
- 第三四分位数(Q3 / 75th Percentile):数据集的中位数和最大值之间的中间值(不是“最大值”);
- 四分位间距(IQR):第25至第75个百分点的距离;
- 晶须(蓝色显示);
- 离群值(显示为绿色圆圈);
- “最大”:Q3 + 1.5 * IQR;
- “最低”:Q1 -1.5 * IQR。
(图片来源于网络)
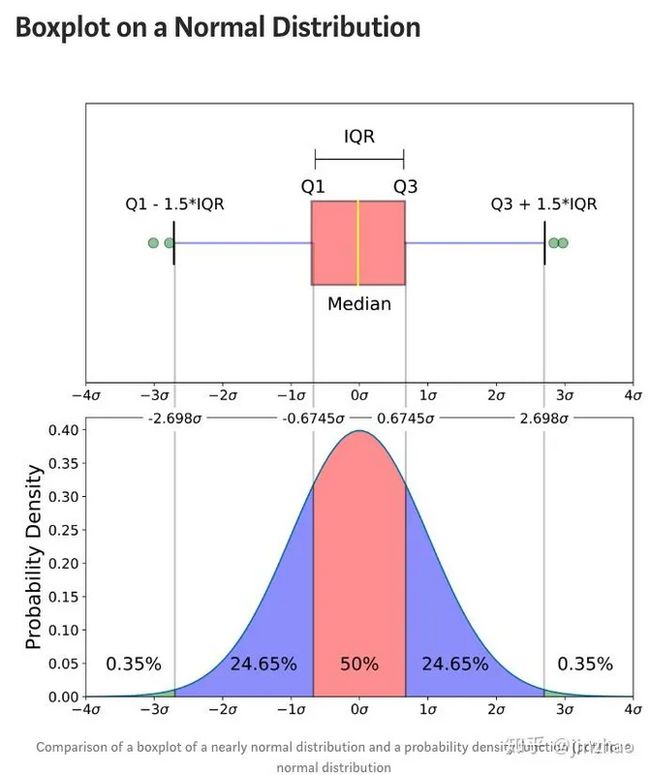
上图是近似正态分布的箱线图与正态分布的概率密度函数(pdf)的比较, 两侧0.35%的数据就能够被视为异常数据。
回到这次的监控方案,由中位数向两边扩散,划分一级二级三级四级五级数据,传入连续时间段内指标的同环比,根据同环比分布的区间确定四个异常类型:异常上涨(同环比分布同时大于等于正三级)、异常(同环比分布在一正一负大于等于三级的范围)、异常下降(同环比分布低于等于负三级)、无异常(同环比分布低于三级的范围)。
三、落地
实现三部曲
1. 代码实现
/*
*数据分析API服务
*/
public class DataAnalysis{
/*
*波动分析
*input:json,分析源数据(样例)
{
"org_data": [
{ "date":"2020-02-01", "data":"10123230" }, 日期类型、long类型
{ "date":"2020-02-02", "data":"9752755" },
{ "date":"2020-02-03", "data":"12123230" },
.......
]
}
*output:json,分析结果
{
"type": 1, --调用正常返回1,异常返回0
"message":"", --异常原因
"date": 2020-02-14,--输入数据中按日期升序排列的最后一组的日期
"data": 6346231,--输入数据中按日期升序排列的最后一组的数据值
"rate1": -0.3,--同比值
"rate2": -0.6,--环比值
"level1": 4,--同比等级,5个类型:1、2、3、4、5
"level2": 3,--环比等级,5个类型:1、2、3、4、5
"result":"异常下降",--四个类型:异常上涨、异常、异常下降、无异常
}
*/
public String fluctuationAnalysis (String org_data){
//第一步,校验输入数据
if(checkOrgdata(org_data)) return {"result": 0, "message":""}
//第二步,计算同环比
computeOrgdata(org_data)
//第三步,数据升序排序,获取数组大小、最后数据中按日期升序排列的最后一组
//以上面样例为了,数组大小14,最后一组数据{ "date":"2020-02-14", "data":"6346231" ,同比:-0.3,环比:-0.6}对同比、环比、(data暂不做)分别做如下处理
-------
//第四步,按照数据升序排序及数据大小,将数据(不算上面找出的最后一组数据)平均分为4等份(这样会在数组中插入三个桩),并计算出第一个桩和第三个桩的值,以上面为例子,原来数组大小14,去掉最后一个,13个
//判断,给结论(1) 如果同比等级> 2 and 环比等级 > 2 (表示一定有异常)
/*
*数据分析API服务
*/
public class DataAnalysis{
/*
*波动分析
*input:json,分析源数据(样例)
{
"org_data": [
{ "date":"2020-02-01", "data":"10123230" }, 日期类型、long类型
{ "date":"2020-02-02", "data":"9752755" },
{ "date":"2020-02-03", "data":"12123230" },
.......
]
}
*output:json,分析结果
{
"type": 1, --调用正常返回1,异常返回0
"message":"", --异常原因
"date": 2020-02-14,--输入数据中按日期升序排列的最后一组的日期
"data": 6346231,--输入数据中按日期升序排列的最后一组的数据值
"rate1": -0.3,--同比值
"rate2": -0.6,--环比值
"level1": 4,--同比等级,5个类型:1、2、3、4、5
"level2": 3,--环比等级,5个类型:1、2、3、4、5
"result":"异常下降",--四个类型:异常上涨、异常、异常下降、无异常
}
*/
public String fluctuationAnalysis (String org_data){
//第一步,校验输入数据
if(checkOrgdata(org_data)) return {"result": 0, "message":""}
//第二步,计算同环比
computeOrgdata(org_data)
//第三步,数据升序排序,获取数组大小、最后数据中按日期升序排列的最后一组
//以上面样例为了,数组大小14,最后一组数据{ "date":"2020-02-14", "data":"6346231" ,同比:-0.3,环比:-0.6}
对同比、环比、(data暂不做)分别做如下处理
-------
//第四步,按照数据升序排序及数据大小,将数据(不算上面找出的最后一组数据)平均分为4等份(这样会在数组中插入三个桩),并计算出第一个桩和第三个桩的值,以上面为例子,原来数组大小14,去掉最后一个,13个
//判断,给结论
(1) 如果同比等级> 2 and 环比等级 > 2 (表示一定有异常)
And
case when 同比值<0 and 环比值<0 then '异常下降'
when 同比值>0 and 环比值>0 then '异常上涨'
else '异常'
end as res
return(2)其他,无异常波动
}
public bool checkOrgdata (String org_data){
//检验数组中日期是否全部连续,数量至少要14天数据
…
if(日期不连续 || 数量小于14)
return false;
return ture;
}
public String computeOrgdata (String org_data){
// 计算输入数据中,每一行的同环比环比=(今日data/昨日data-1)*100%,
同比=(今日data/上周同日data-1)*100%
return
{
"org_data": [
{ "date":"2020-02-01", "data":"10123230" ,同比:null,环比:null },
{ "date":"2020-02-02", "data":"9752755" ,同比:null,环比:0.9},
{ "date":"2020-02-03", "data":"12123230" ,同比:null,环比:0.9},
.......
]
}
}对于输入数据的几个关键点:
(1)要求是连续的日期,并且至少14天的数据,建议100天的数据
(2)api中当同环比计算为null时,统一处理为0
(3)当传入的数量大于90天,取最近90天作为样本,当数量小于90天,拿所有上传作为样本
2. API封装
(1)提供已封装好的API服务为大家使用:
API使用:
传入数据示例(json)
{
"org_data": [
{ "date":"2020-02-01", "data":"10123230" ,同比:null,环比:null },
{ "date":"2020-02-02", "data":"9752755" ,同比:null,环比:0.9},
{ "date":"2020-02-03", "data":"12123230" ,同比:null,环比:0.9},
.....
]
}返回结果解释:
{
"type": 1, --调用正常返回1,异常返回0
"message":"", --异常原因
"date": 2020-02-14,--输入数据中按日期升序排列的最后一组的日期
"data": 6346231,--输入数据中按日期升序排列的最后一组的数据值
"rate1": -0.3,--同比值
"rate2": -0.6,--环比值
"level1": 4,--同比等级,5个类型:1、2、3、4、5
"level2": 3,--环比等级,5个类型:1、2、3、4、5
"result":"异常下降",--四个类型:异常上涨、异常、异常下降、无异常
}注意问题点:
对于输入数据的几个关键点:
(1)要求是连续的日期,并且至少14天的数据,建议100天的数据
(2)api中当同环比计算为null时,统一处理为0
(3)当传入的数量大于90天,取最近90天作为样本,当数量小于90天,拿所有上传作为样本
3. JAR 包提供
大数据中心日常数据开发工作以HQL为主,我们将API服务封装成JAR包,可直接适用于数仓开发使用。
四、运用场景
目前成功运用于大数据中心多个重点业务和平台,对其日常指标进行监控,以应用商店为例。
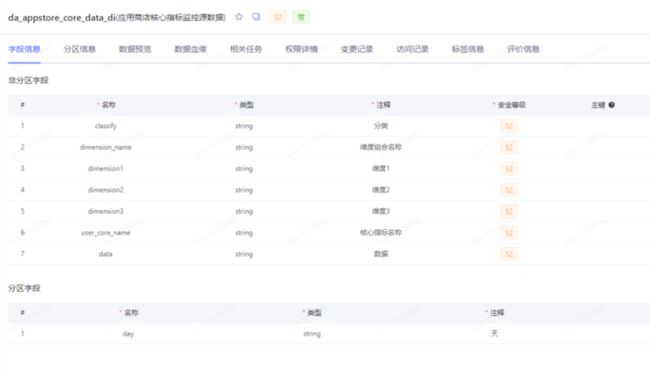
1、获取da表数据到 da\_appstore\_core\_data\_di
2、监控数据统一处理 da\_appstore\_core\_data\_result_di
3、每条记录调用上述UDF函数,输出判定结果,异常值可对业务发送提醒,帮助排除业务风险
参考文献
- 《创世纪·数理统计·正态分布的前世今生》
- 知乎朋友-小尧、jinzhao 关于正态分布阈值原理的部分阐述
作者:vivo 互联网大数据团队