基于Matpower的电力系统潮流计算设计原理
基于Matpower的电力系统潮流计算设计原理
- 第一部分 前言
- 第二部分 牛顿-拉夫逊算法潮流计算的基本原理
-
- 1.牛顿-拉夫逊计算法潮流计算原理
- 2.牛顿-拉夫逊计算法潮流直角坐标计算原理
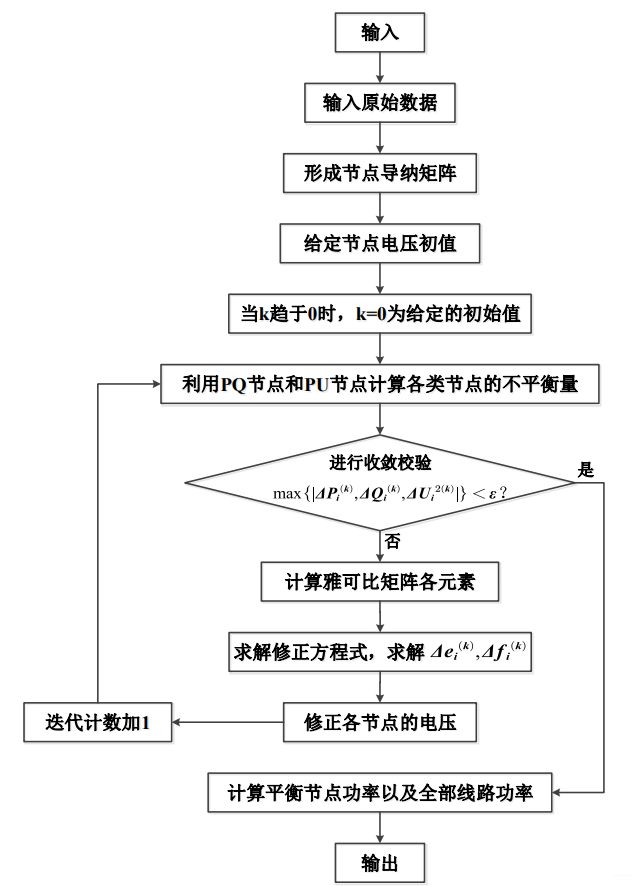
- 3.牛顿-拉夫逊计算法潮流计算流程
- 第三部分 Matpower仿真软件
-
- 1.Matpower软件简介
- 2.Matpower矩阵参数
- 第四部分 电力系统节点导纳矩阵
-
- 1.节点导纳矩阵简介
- 2.节点导纳矩阵仿真运算
第一部分 前言
电力系统分析中, 潮流计算的意义十分重大,它是在电网正常或故障情况下的稳定运行状态的计算,为了更加深入地理解潮流计算,本文基于牛顿-拉夫逊潮流计算原理,设计出一个8机28节点的电力系统网络结构,然后基于Matlab进行仿真运行分析。
各类配电网潮流算法性能通常从以下几个方面进行分析: 算法的收敛速度、稳定性、算法的复杂程度。潮流计算的稳定性对于维护电力系统稳定潮流计算。它根据给定的初始值和网络结构确定整个系统的运行状态, 确定各个母线上的电压幅值及相角、网络中的功率分布以及网络损耗等。潮流计算的基本方程是由电力系统的网络方程得到的。在电力系统中都存在一些静态装置, 例如变压器、输电线路、并联电容器和电抗器等, 它们可以由电阻、电感和电容等基础元件构成的等值电路来模拟。
第二部分 牛顿-拉夫逊算法潮流计算的基本原理
牛顿-拉夫逊法实质上就是切线法,是逐步线性化的方法。牛顿-拉夫逊计算法不仅用于求解单变量方程,还可以求解多变量非线性代数方程。
1.牛顿-拉夫逊计算法潮流计算原理
设有单变量非线性方程
![]()
在求解此方程的时候,需要先给出解的近似值 x ( 0 ) x^{(0)} x(0),它的与真解的误差将满足下列方程式
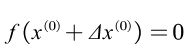
将上述式子左边的函数在 x ( 0 ) x^{(0)} x(0)附近展开成泰勒级数得到:
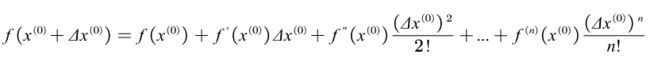
如果差值 的值很小,差值的二次及以上阶次的各项均可以省去,于是可以简化成:
![]()
这是对于变量的修正量线性方程式(修正方程式),据此可以得到修正量
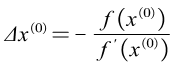
但是修正后的近似解 x ( 1 ) x^{(1)} x(1)与真解仍然存在误差,为了进一步逼近真解,可以一直迭代下去,最终可以得到迭代计算通式:
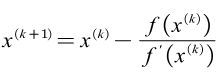
而迭代过程中的收敛判据为:
![]()
![]()
由此可见,牛顿-拉夫逊法实质上就是切线法,是逐步线性化的方法。牛顿-拉夫逊计算法不仅用于求解单变量方程,还可以求解多变量非线性代数方程。
设有n个联立的非线性代数方程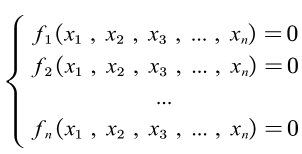
假定已经给出各变量的初值 x 1 ( 0 ) x1^{(0)} x1(0), x 2 ( 0 ) x2^{(0)} x2(0),…, x n ( 0 ) x n^{(0)} xn(0),令![]()
分别为各个变量的修正量,使其满足方程组,即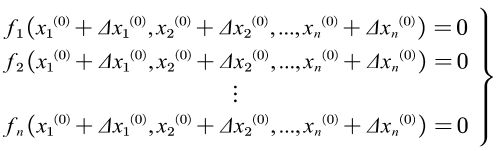
将n个多元函数在初始值附近分别展开成泰勒级数,并略去二次及以上阶次的各项,可以得到牛顿-拉夫逊法的修正方程式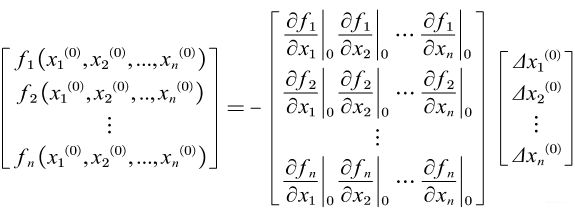
利用高斯消去法或者三角分解法可以解出修正量,然后对初始值近似解进行修正![]()
如此反复迭代,在进行第k+1次迭代时,从而求出修正方程式: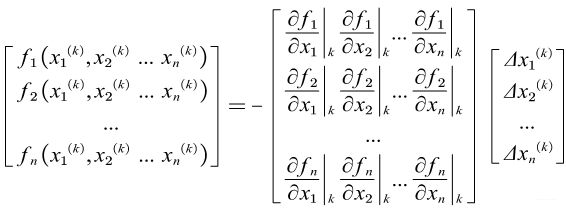
得到修正量![]()
并对各变量进行修正,最终可以表示为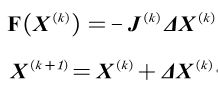
其中,** X X X**是由n个变量组成的n维矩阵列向量, F ( X ) F(X) F(X),是由n个多元函数组成的n维向量: J J J是n*n阶方阵,称为雅可比矩阵。迭代过程一直进行到满足收敛判据![]()
2.牛顿-拉夫逊计算法潮流直角坐标计算原理
由于节点电压可以采用不同的坐标系表示,牛顿-拉夫逊潮流计算也将相应地采用不同的计算公式。
采用直角坐标时,节点电压可以表示为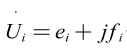
导纳矩阵元素可以表示为![]()
假定系统中的第1,2,…,m号节点为PQ节点,第i个节点的给定功率设为 P i s Pis Pis和 Q i s Qis Qis,对于该节点可以写出如下方程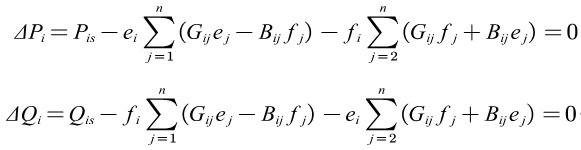
假定系统中的第m+1,m+2,…,n-1号节点为PU节点,对于其中每一个节点可以写出如下方程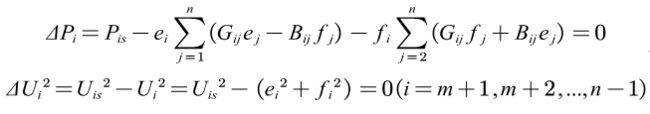
第n号节点为平衡节点,其中电压![]()
是给定的,所以不参加迭代,对于PQ节点方程式和PU节点方程式来说,总共包含2(n-1)个方程式,带求的变量也是2(n-1)个,因此,我们可以得到如下的修正方程式![]()
![]()
![]()
其中修正方程式还可以写成分块矩阵的形式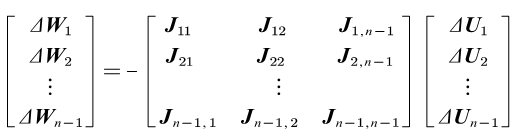
其中,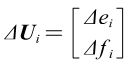
对于PQ节点
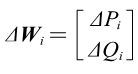
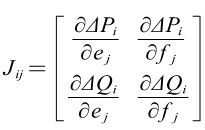
对于PU节点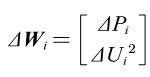
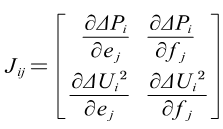
雅可比矩阵各元素都是节点电压的函数,它们的数值将在迭代的过程中不断地改变,因此在用牛顿-拉夫逊法计算潮流首先要输入网络的原始数据以及各节点的给定值并且形成节点导纳矩阵,输入节点电压初值,设置迭代计数k=0,然后开始进入牛顿-拉夫逊算法的迭代过程。
3.牛顿-拉夫逊计算法潮流计算流程
第三部分 Matpower仿真软件
1.Matpower软件简介
MATPOWER是基于 Matlab 语言的m文件组建包,作为电力系统潮流计算仿真软件。潮流计算仿真中,按照MATPOWER中潮流计算程序的格式修改或重新编写一个新的程序“caseX.m”,在MATLAB软件中的命令窗口输入runpf(‘程序名’)就可以通过MATPOWER已经编好的程序进行潮流计算,而通过调用函数runpf的参数计算潮流。2.Matpower矩阵参数
(1) baseMVA
baseMVA是一个标量,用来设置基准容量。对于计算中采用有名值,可以根据实际情况设置,在本文设计中设置为100MVA。
(2) bus data矩阵
bus矩阵是关于电网母线节点参数设计的矩阵,通过设置母线的参数来达到计算的目的,如表3.1所示,bus data有如下参数
| Bus_i | type | Pd | Qd | Gs | Bs | Area | Vm | Va | baseKV | zone | Vmax | Vmin |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 97.6 | 44.2 | 0 | 0 | 1 | 1.0393896 | -13.5366 | 311 | 1 | 1.06 | 0.94 |
其中,各项参数的含义为:
- bus_i用来设置母线编号,范围为1~29997。
- type用来设置母线类型,1为PQ节点,2为PV节点,3为平衡节点;
- Pd用来设置母线注入负荷的有功功率
- Qd用来设置母线注入负荷的无功功率
- Gs用来设置与母线并联的电导
- Bs用来设置与母线并联的电纳
- area 用来设置电网断面号,可设置范围为1~100,一般设置为1
- Vm用来设置母线电压的幅值初值
- Va用来设置母线电压的相角初值
- baseKV用来设置该母线的基准电压
- zone用来设置省耗分区号,可设置范围为1~999,一般设置为1
- Vmax用来设置工作时母线电压最高幅值
- Vmin用来设置工作时母线电压最低幅值
(3) generator data矩阵
generator data矩阵是用来设置电网中发电机的参数,各项参数名称如表3.2所示:
| Bus | Pg | Qg | Qmax | Qmin | Vg | mBase | status | Pmax | Pmin | Pc1 | Pc2 | Qc1min | Qc1max | Qc2min | Qc2max | amp_agc | Ramp_10 | Ramp_30 | Ramp_q |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 17 | 650 | 207 | 300 | 150 | 1.05256 | 100 | 1 | 725 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
其中,
-
bus用来设置接入发电机的母线编号
-
Pg用来设置接入发电机的有功功率,注意功率输入的是有名值
-
Qg用来设置接入发电机的无功功率
-
Qmax用来设置接入发电机的无功功率的最大允许值
-
Qmin用来设置接入发电机的无功功率的最小允许值
-
Vg用来设置接入发电机的工作电压,注意输入的是标幺值
-
mBase用来设置接入发电机的功率基准
-
status用来设置发电机的工作状态,1表示投入运行,2表示投出运行
-
Pmax用来设置接入发电机的无功功率的最大允许值
-
Pmin用来设置接入发电机的无功功率的最小允许值
-
其余的Pc1,Pc2,Qc1min,Qc1max,Qc2min,Qc2max,ramp_agc,ramp_10,ramp_30,ramp_q,apf均表示发电机其他特征量,在实际计算中可以设置为0
(4) branch data矩阵
brach data是一个矩阵,用来设置电网中各个支路之间的参数,矩阵参数名称如表3.3所示:
| fbus | tbus | r | x | b | rateA | rateB | rateC | ratio | angle | Status | angmin | angmax |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 0.0035 | 0.0411 | 0.6987 | 600 | 600 | 600 | 0 | 0 | 1 | -360 | 360 |
其中,
- fbus用来设置支路起始节点编号
- tbus用来设置支路终止节点编号
- r用来设置该支路电阻,注意阻抗导纳等参数输入的都是标幺值
- x用来设置该支路电抗
- b用来设置该支路电纳
- rateA用来设置该支路长期允许功率
- rateB用来设置该支路短期允许功率
- rateC用来设置该支路紧急允许功率
- ratio用来设置该支路变比,若该支路仅仅为导线则设置为0,若含有变压器,则该变比为fbus侧母线基准电压与tbus侧基准变压之比
- angle用来设置支路的相位角度,如果支路元件为变压器,则就是变压器的转角,如果支路元件不是变压器,则相位角度为0度
- status用来设置支路工作状态,1表示投入运行,0表示退出运行
(5) generator cost data矩阵
一般来说,generator cost data矩阵保持原有默认的设计,不作修改。
基于Matpower的潮流计算矩阵的设计,需要改变如上矩阵的参数,使其满足收敛条件,最终得到相应的计算结果,因此熟悉Matpower矩阵的编写对于最终的仿真结果有着极其重要的意义。
第四部分 电力系统节点导纳矩阵
1.节点导纳矩阵简介
电力网络中的运行状态可以用节点方程或者回路方程进行描述,节点方程以母线电压作为待求量,节点方程的求解结果对于潮流计算应用广泛。
一般地,对于有n个独立节点的网络,可以列写出n个节点方程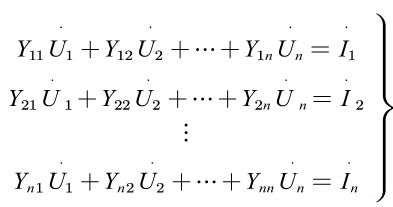
可以写成矩阵形式
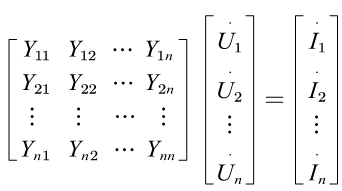
矩阵Y称为节点导纳矩阵,其对角线元素Y称为节点i的自导纳,等于接于节点i的所有支路导纳之和,非对角线元素成为节点ij之间的互导纳,等于直接连接于节点ij之间的支路导纳的负值,如果节点ij之间不存在直接支路,则导纳为0,因此,节点导纳矩阵是一个稀疏的对称矩阵。
2.节点导纳矩阵仿真运算
基于上述原理,编写出电力系统的节点导纳矩阵的计算代码
N1=input('输入节点数,N1=');
L1=input('输入支路数,L1=');
Y=zeros(N1);G=zeros(N1);B=zeros(N1);
B1=[ 1 2 0.0035 0.0411 0.6987 600 600 600 0 0 1 -360 360;
1 14 0.0023 0.0353 0.3804 900 900 900 0 0 1 -360 360;
1 27 0.0014 0.025 0.75 1000 1000 1000 0 0 1 -360 360;
2 3 0.0013 0.0213 0.2214 500 500 500 0 0 1 -360 360;
2 28 0.0067 0.0086 0.146 500 500 500 0 0 1 -360 360;
3 4 0.0013 0.0151 0.2572 500 500 500 0 0 1 -360 360;
3 12 0.0011 0.0133 0.2138 500 500 500 0 0 1 -360 360;
4 5 0.0004 0.0046 0.078 900 900 900 0 0 1 -360 360;
4 20 0.0022 0.035 0.361 600 600 600 0 0 1 -360 360;
5 6 0 0.025 0 1800 1800 1800 1.07 0 1 -360 360;
5 25 0.002 0.0353 0.3804 900 900 900 0 0 1 -360 360;
5 12 0.004 0.0232 0.531 600 600 600 0 0 1 -360 360;
6 7 0.0016 0.0435 0 500 500 500 1.06 0 1 -360 360;
6 18 0.0004 0.043 0.729 600 600 600 0 0 1 -360 360;
7 8 0.0009 0.0094 0.171 600 600 600 0 0 1 -360 360;
7 13 0.0016 0.0435 0 500 500 500 1.06 0 1 -360 360;
8 23 0.0018 0.0217 0.366 600 600 600 0 0 1 -360 360;
9 10 0.0007 0.0089 0.1342 600 600 600 0 0 1 -360 360;
9 19 0.0003 0.0059 0.068 600 600 600 0 0 1 -360 360;
10 11 0.0007 0.0082 0.1319 600 600 600 0 0 1 -360 360;
10 18 0.0013 0.0173 0.3216 600 600 600 0 0 1 -360 360;
11 12 0.0008 0.014 0.2565 900 900 900 0 0 1 -360 360;
12 16 0.0032 0.0323 0.531 600 600 600 0 0 1 -360 360;
13 17 0.0006 0.0232 0 900 900 2500 0 0 1 -360 360;
14 20 0.0057 0.0625 1.029 600 600 600 0 0 1 -360 360;
15 19 0.0043 0.0474 0.7802 600 600 600 0 0 1 -360 360;
20 17 0.0014 0.0151 0.249 600 600 600 1.032 0 1 -360 360;
21 22 0.0014 0.0147 0.2396 600 600 600 0 0 1 -360 360;
22 23 0.0008 0.0156 0 1200 1200 2500 1.25 0 1 -360 360;
23 18 0.0006 0.0096 0.1846 0 0 0 0 0 1 -360 360;
23 24 0 0.0143 0 900 900 2500 1.25 0 1 -360 360;
24 25 0.0032 0.0323 0.531 600 600 600 0 0 1 -360 360;
25 26 0.0005 0.0272 0 900 900 2500 0 0 1 -360 360;
26 27 0.0006 0.0232 0 900 900 2500 1.25 0 1 -360 360;
27 28 0.0043 0.0474 0.7802 600 600 600 0 0 1 -360 360;];
for m1=1:N1
I=B1(m1,1);
J=B1(m1,2);
R=B1(m1,3);
X=B1(m1,4);
k=B1(m1,5);
if I*J==0
if I==0
G(j,J)=G(J,J)+R;
B(J,J)=B(J,J)+X;
else
G(I,I)=G(I,I)+R;
B(I,I)=B(I,I)+X;
end
elseif I*J>0
B(I,I)=B(I,I)+k;
B(J,J)=B(J,J)+k;
k=1;
else
if I<0
t=I;
I=J;
J=t;
end
J=abs(J);
36
if k<0
k=-1/k;
end
end
G(I,J)=-(1.0/k)*R/(R^2+X^2);
B(I,J)=(1/k)*X/(R^2+X^2);
G(J,I)=G(I,J);
B(J,I)=B(I,J);
G(I,I)=G(I,I)+R/(R^2+X^2);
B(I,I)=B(I,I)-X/(R^2+X^2);
G(J,J)=G(J,J)+1/(k^2)*R/(R^2+X^2);
B(J,J)=B(J,J)-1/(k^2)*R/(R^2+X^2);
Y=G+i.*B
end
Y
得到如下所示的结果
第1—8行节点导纳矩阵
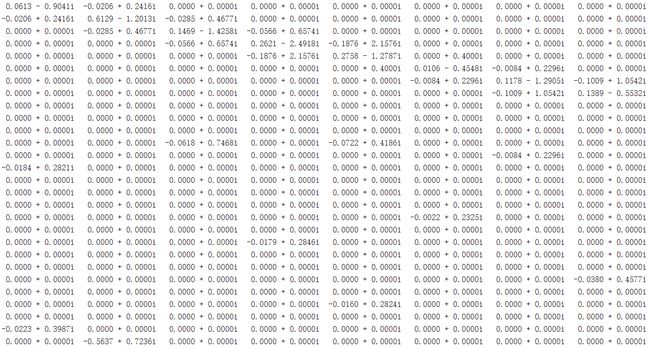
第9—16行节点导纳矩阵
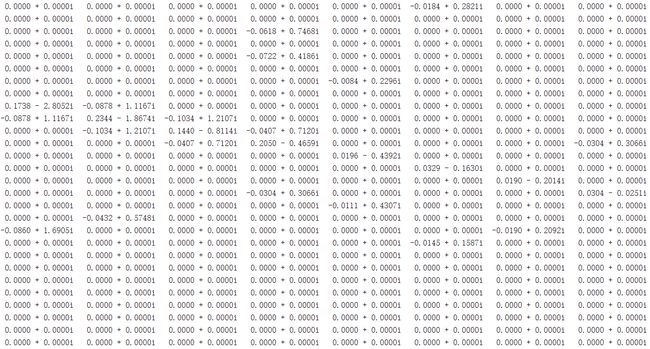
第17—24行节点导纳矩阵
第25—28行节点导纳矩阵

根据图示结果可以看出,导纳矩阵是稀疏矩阵,它的对角线元素一般不为0,但在非对角线元素中会存在0,在电力系统的接线图中,一般每个节点同平均不超过3到4个其他节点有直接连接的支路,因此在导纳矩阵中的非对角线元素中每行平均仅有3到4个非0元素,其余都是零元素,第1-28列数据大部分都为零元素,每行仅有少数是非零元素,符合节点导纳矩阵规律。
最终基于上述原理并结合Matpower,可以得到以下仿真结果
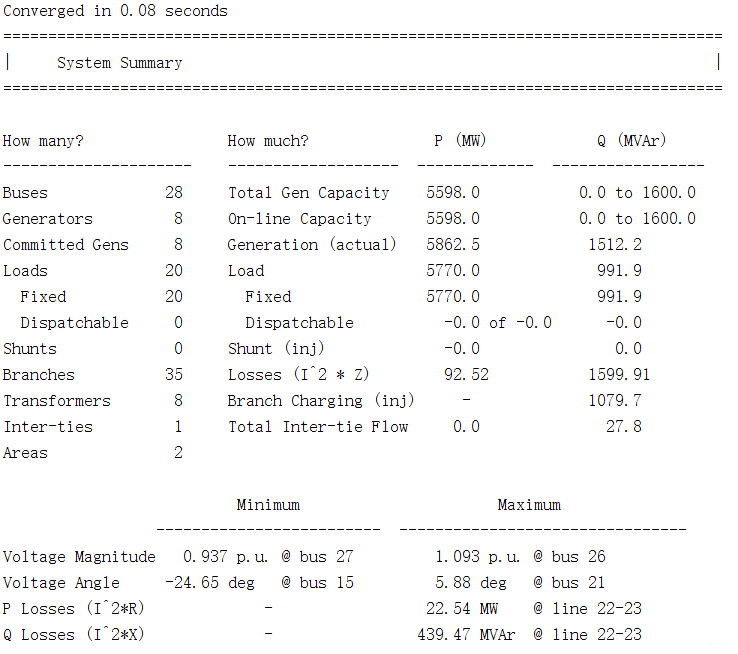
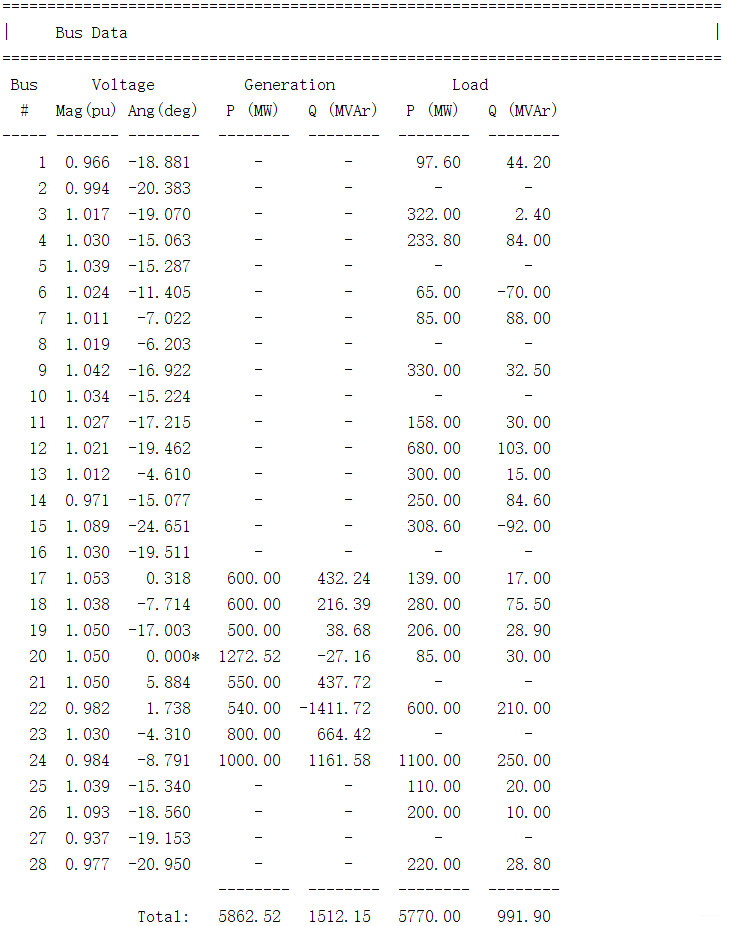
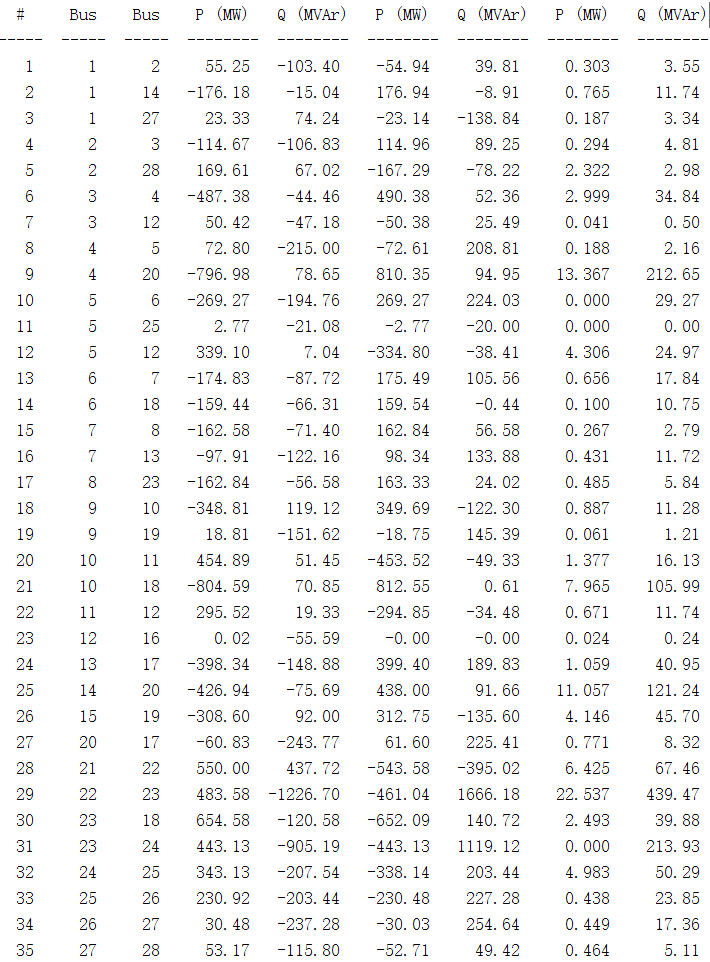
以上就是本次要讲的内容,本文仅仅简单介绍了潮流计算的相关理论知识,而利用Matpower能使我们快速便捷地处理数据,最终得到想要的结果。
具体的仿真结果可以继续参照文章——基于Matpower的电力系统潮流计算仿真
根据这篇文章可以得到基于Matpower的电力系统潮流计算仿真结果,与本文相结合可以加深对于潮流计算的理解。
同样的,可以参考网址——https://blog.csdn.net/Gentleheng/article/details/112782403