R语言之主成分分析和因子分析
一、概念
1.主成分分析
- 定义:主成分分析(principal components analysis)是从多个数值变量(指标)之间的相互关系入手,利用降维的思想,将多个变量(指标)化为少数几个互不相关的综合变量(指标)的统计方法。
- 目的:①综合变量尽可能多地反映原来资料的信息;②彼此之间相互独立。
- 重要术语:主成分的贡献率及累积贡献率、成分载荷、成分公因子方差、成分唯一性、Kaiser-Harris准则、Cattell碎石检验、平行分析、主成分得分
- 了解更多:如何通俗易懂地讲解什么是 PCA 主成分分析?以及含数学公式推导的主成分分析原理
2.因子分析
- 定义:因子分析(factor analysis)是一种从多个原始指标的相关关系入手,找出支配这种相关关系的有限个不可观测的潜在变量,并用这些潜在变量来揭示原始指标之间的相关性或协方差关系的多元统计分析方法。
- 分类:探索性因子分析(exploratory factor analysis)、验证性因子分析(confirmatory factor analysis)。多用前者,是一系列用来发现一组变量的潜在结构的方法。
- 重要术语:公共因子、特殊因子、公共度、因子贡献及因子贡献率、因子载荷、主轴迭代法、极大似然法、因子旋转
- 了解更多:因子分析定义和应用以及因子分析的概念
二、PCA和EFA的比较
| 主成分分析 | 因子分析 |
|---|---|
| 原始变量的线性组合构成成分 | 因子的线性组合组成原始变量 |
| 成分彼此独立(正交),可能难以解释 | 因子的解释很重要,有时会牺牲方差或独立性假设 |
| 重在综合原始变量的信息 | 重在解释原始变量之间的关系 |
| 将原始坐标轴在空间上进行旋转 | 将原始变量的信息分块 |
| 不需旋转 | 按需旋转 |
| 联系 |
|---|
| 对"原始变量之间存在着较强的线性相关关系"进行假设检验 ,如KMO、Bartlett’s球状检验 |
| 判断主成分和公共因子个数的方法相同,如Kaiser-Harris准则、Cattell碎石检验、平行分析 |
| 成分(系数)和因子(载荷)的解释类似 |
| 系数是主成分和变量之间相关性的定量度量, 载荷是因子对原始变量的影响 |
| 因子分析的主成分解与主成分分析的结果完全一致 |
三、R语言实例
读取数据:
setwd('E:/R/R files')
score <- read.csv('E:/R/R files/PCAscore.csv')
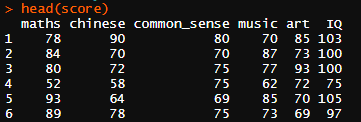
head(score)
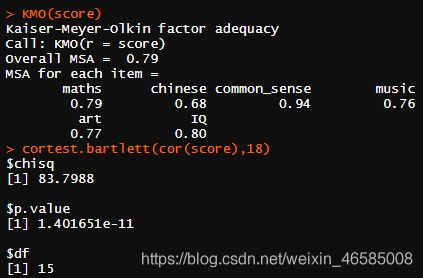
- KMO检验:
KMO>0.9强相关性,>0.8较强相关性,>0.7中等程度相关性;KMO<0.5则不可接受。此处KMO=0.79接近0.8,相关性较强,支持PCA和EFA。 - Bartlett’s球状检验:P<0.05则有统计学意义,各变量具有相关性,支持PCA和EFA。
- 主成分分析
2.1首先,判断主成分个数
library(psych)
fa.parallel(score,n.obs = 18,fa = 'pc',show.legend = FALSE,main='Scree plot with parallel analysis')
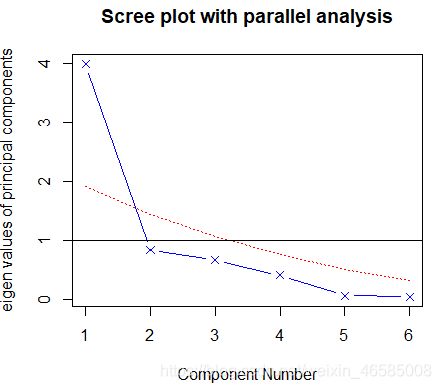
碎石图、特征值大于1准则和100次模拟的平行分析都表明保留一个主成分即可。(但是某些时候这三个方法的结果并不一致,或者最终得到的主成分解释度较低,此时需要根据实际情况提取不同数目的主成分,选择最优方案)
2.2其次,提取主成分
pc <- principal(score,nfactors = 1,rotate = 'none')
pc
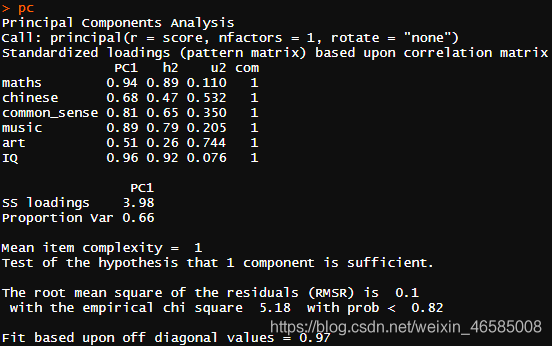
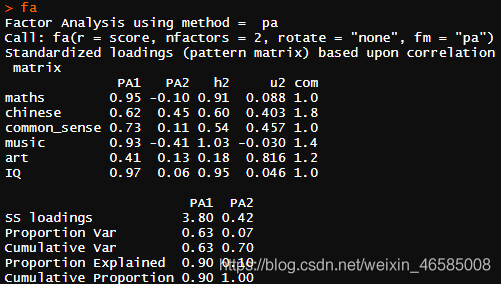
PC1为成分载荷,可了解各主成分与各原始指标之间的关系。第一主成分与数学、常识、音乐、智商高度相关,而与语文和美术中等程度相关。
h2为成分公因子方差,u2为成分唯一性。举例,智商92%的方差都可由第一主成分来解释,8%不能,因此智商是用第一主成分表示性最好的变量,美术为最差的。
SS loadings为与主成分相关的特征值。
Proportion Var表示每个主成分对整个数据集的解释程度。此处,第一主成分解释了6个变量66%的方差。
此处第一主成分对方差的贡献率仅66%,未达到一般要求的70%(注:不同教材、文献对此数据报道不同,亦见80%、85%),若增加主成分个数到2个,累积贡献率增加到80%,此时第一主成分反映了除美术外各学科的综合成绩,第二主成分反映美术的成绩。因此,主成分个数的选择没有绝对唯一的标准,统计分析和专业意见须同时考虑。
2.3最后,主成分得分
pc <- principal(score,nfactors = 2,rotate = 'none',scores = TRUE)
head(pc$scores)
round(unclass(pc$weights),2)
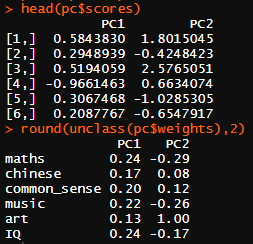
scores即为各观测对象的得分。
weights即为各指标的权数,也即每个主成分所对应的特征向量。由此可写出PC1和PC2的表达式,计算scores(需将各指标进行标化处理)。
2.4综合评价函数
求出主成分后,选择累积贡献率已达较高的前m个主成分,以每个主成分的贡献率作为权数,构造出综合评价函数。
![]()
关于此函数有无意义在不同教材存在争议。
通过构造主成分的线性组合来产生一个综合指标,本质上完全不同于由原始变量的线性组合产生的综合指标,后者只要加权得合理且有意义完全可行。这是因为,原始变量的含义是实在的、确切的,这是看懂和理解线性组合含义的基础;而主成分是人为定义的、意义含糊的(可以有无数个与主成分解释相同的线性组合),并不像原始变量那样具有实质意义。
- 探索性因子分析
3.1 首先,判断提取的公共因子数
> library(psych)
> fa.parallel(score,n.obs = 18,fa = 'both',main='Scree plot with parallel analysis')
Parallel analysis suggests that the number of factors = 1 and the number of components = 1
fa = 'both’则同时展示主成分和公共因子分析的结果。
此时发现,R建议提取公共因子数为1(主成分也为1)。
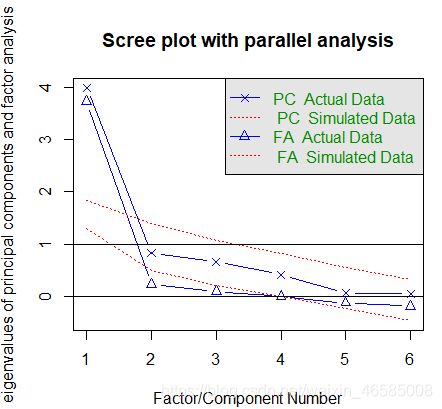
此处发现,三个准则结果不一致,结合实际选取2个公共因子,看看能不能找出2个潜在的结构来解释变量关系(至于分析结果,呵呵)。
3.2 提取公共因子
fa <- fa(score,nfactors=2,rotate='none',fm='pa')
> fa <- fa(score,nfactors=2,rotate='none',fm='pa')
Warning messages:
1: In fa.stats(r = r, f = f, phi = phi, n.obs = n.obs, np.obs = np.obs, :
The estimated weights for the factor scores are probably incorrect. Try a different factor score estimation method.
2: In fac(r = r, nfactors = nfactors, n.obs = n.obs, rotate = rotate, :
An ultra-Heywood case was detected. Examine the results carefully
尝试更换提取公共因子的方法,选用极大似然法(ml),警告消失:
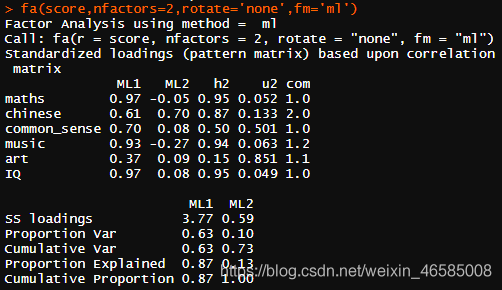
发现对方差解释的累积贡献率增加了3%。
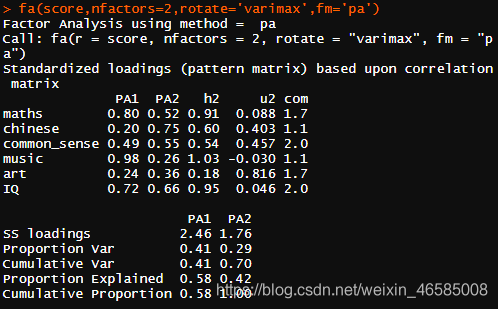
根据因子载荷矩阵,数学、常识、音乐、艺术和智商在第一因子上载荷较大,语文在第二因子上载荷较大。
寻找公共因子的主要目的在于弄清各公共因子的专业意义,以便对实际问题进行分析。
尝试解释为,存在一个理性智力因子,感性智力因子。毕竟第一因子的几个变量都需要更多的理性思维吧(记谱、创作等还是需要理性,不要告诉我音乐、艺术感性更多,我不听!!!)。好吧,如果觉得解释牵强,那么进行因子旋转吧!
3.3 因子旋转
选用最常见的方差最大法/正交旋转(varimax试试看。
Warning messages:
1: In fa.stats(r = r, f = f, phi = phi, n.obs = n.obs, np.obs = np.obs, :
The estimated weights for the factor scores are probably incorrect. Try a different factor score estimation method.
2: In fac(r = r, nfactors = nfactors, n.obs = n.obs, rotate = rotate, :
An ultra-Heywood case was detected. Examine the results carefully
很不给面子,直接警告:出现超海伍德现象(这是个什么鬼啊啊啊!!!)
运用ML方法容易受到海伍德现象的影响。在因素分析中,共同度是相关系数的平方,因此应该居于0~1之间。这是公共因素模型的数学特征,然而,共同度的估计值可能会超过1.如果共同度等于1,就称为海伍德现象,若超过1,称为超海伍德现象。海伍德现象和超海伍德现象意味着某些独特因子的方差为负,表明肯定存在问题。
可能的原因:①共同度估计的问题。②公共因素太多。③公共因素太少。④数据太少不能提供稳定的估计。⑤公共因素模型不适合这些数据。
此处怀疑,警告原因为③和/或④,毕竟前面R就提醒选取1个公共因子就行,但是这样根本找不出来潜在的结构,是我多情了(手动再见,好的,我也开始怀疑这个数据集本身就分析不出个啥)
3.4因子分析可视化
使用factor.plot()或fa.diagram()函数:
factor.plot(fa,labels = rownames(fa.quartimax$loadings))
fa.diagram(fa,simple = FALSE)
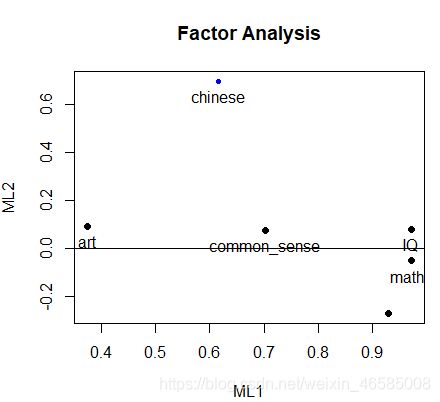
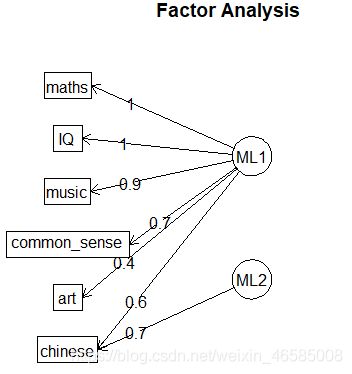
好的,就分析到这里了,主要是对R语言psych包提供的函数进行运用,以加深对PCA和EFA的理解。(选用的数据集实在不给力啊~)
3.5注意
- 处理实际问题时,提取公共因子的方法不唯一,比如极大似然法、主轴迭代法、加权最小二乘法、广义加权最小二乘法、最小残差法。
- 还可以进行因子旋转获得更为满意的解,需根据专业意义确定,比如正交旋转法、斜交转轴法、四次方最大旋转法、均方最大旋转法等。
四、后记
由于主成分分析与因子分析都是从多个原始变量之间的相关关系入手,寻找各变量之间的共性因素,因此在方法学原理上两种方法之间并没有本质上的差别,只是因子分析再主成分分析的基础上进行了推广。
参考:
1.滕达. 浅谈主成分分析与因子分析方法的联系与区别[J]. 中国新技术新产品,2011(22).
2.杨晓倩. 主成分分析和因子分析的异同讨论[J]. 经贸实践, 2015(7).
3.C.TEST语言能力的探索性因素分析[J]. 黄春霞. 中国考试. 2011(06).
4.颜虹. 医学统计学. 第3版[M]. 2015.