【数据分析】利用机器学习算法进行预测分析（三）：最近邻（K-Nearest Neighbours）（2021-01-17）

时间序列预测中的机器学习方法（三）：最近邻（K-Nearest Neighbours）

本文是“时间序列预测中的机器学习方法”系列文章的第三篇，如果您有兴趣，可以先阅读前面的文章：
【数据分析】利用机器学习算法进行预测分析（一）：移动平均（Moving Average）
【数据分析】利用机器学习算法进行预测分析（二）：线性回归（Linear Regression）

1.引言

先举一个简单的小例子。根据已知的十个人的年龄、身高和体重，推测已知年龄和身高的第十一个人的体重。


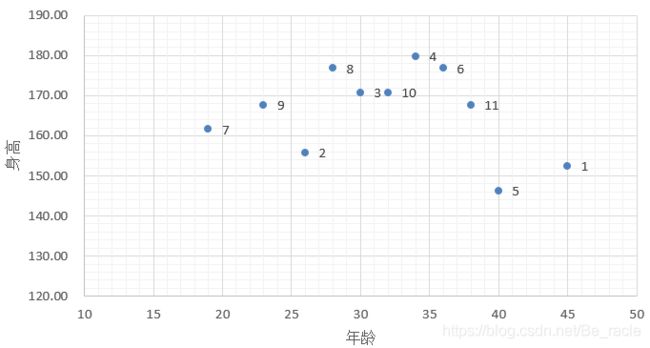
KNN的思想在此处的体现就是选取11号周围人的体重来进行平均。从上图中我们可以看到，在身高和年龄两个维度下，和11比较邻近的有4，6，5，1，如果把聚类的簇大小设置为3，那么我们可以任意选择三个邻近点来计算，比如选择1，5，6：

则由此推断11号的体重为(77+72+60)/3=69.66。

2.基于最近邻算法的股价预测

数据集和前面写的两篇文章相同，目的是为了比较不同算法对同一数据集的预测效果。数据集和代码放在了我的GitHub上，需要的朋友可以自行下载。

导入包，并读入数据。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

# reading the data
df = pd.read_csv('NSE-TATAGLOBAL11.csv')

下面的数据处理操作同上一篇文章线性回归方法类似，此处不再重复。

# setting the index as date
df['Date'] = pd.to_datetime(df.Date,format='%Y-%m-%d')
df.index = df['Date']

#creating dataframe with date and the target variable
data = df.sort_index(ascending=True, axis=0)
new_data = pd.DataFrame(index=range(0,len(df)),columns=['Date', 'Close'])

for i in range(0,len(data)):
     new_data['Date'][i] = data['Date'][i]
     new_data['Close'][i] = data['Close'][i]

#create features
from fastai.tabular import add_datepart
add_datepart(new_data, 'Date')
new_data.drop('Elapsed', axis=1, inplace=True)  #elapsed will be the time stamp

new_data['mon_fri'] = 0
for i in range(0,len(new_data)):
    if (new_data['Dayofweek'][i] == 0 or new_data['Dayofweek'][i] == 4):
        new_data['mon_fri'][i] = 1
    else:
        new_data['mon_fri'][i] = 0

#split into train and validation
train = new_data[:987]
valid = new_data[987:]

x_train = train.drop('Close', axis=1)
y_train = train['Close']
x_valid = valid.drop('Close', axis=1)
y_valid = valid['Close']

导入与最近邻模型有关的包。

#importing libraries
from sklearn import neighbors
from sklearn.model_selection import GridSearchCV
from sklearn.preprocessing import MinMaxScaler 

进行归一化处理。

#scaling data
scaler = MinMaxScaler(feature_range=(0, 1))
x_train_scaled = scaler.fit_transform(x_train) #对x_train进行归一化处理
x_train = pd.DataFrame(x_train_scaled)
x_valid_scaled = scaler.fit_transform(x_valid) #对x_valid进行归一化处理
x_valid = pd.DataFrame(x_valid_scaled)

看一下归一化过后的数据是什么样的。

x_train

利用GridSearchCV寻找最佳参数。

#using gridsearch to find the best parameter
params = {
     'n_neighbors':[2,3,4,5,6,7,8,9]}
knn = neighbors.KNeighborsRegressor()
model = GridSearchCV(knn, params, cv=5)

适应模型并作出预测。

#fit the model and make predictions
model.fit(x_train,y_train)
preds = model.predict(x_valid)

RMSE的大小一定程度上反映了误差大小。

#rmse
rmse = np.sqrt(np.mean(np.power((np.array(y_valid)-np.array(preds)),2)))
rmse 

通过绘图直观地观察预测情况。

#plot
valid['Predictions'] = 0
valid['Predictions'] = preds
plt.figure(figsize=(16,8))
plt.plot(valid[['Close', 'Predictions']])
plt.plot(train['Close'])
plt.show()

可以看到KNN在这个数据集上的预测效果并不是很好。