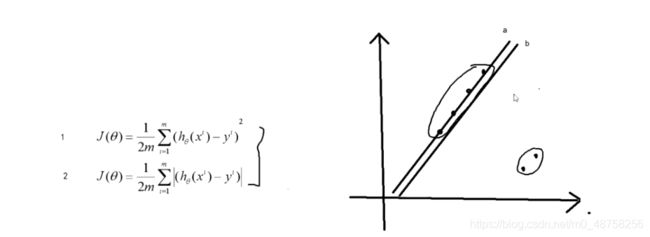2021.1.21线性回归算法的原理及参数优化方案

只需要知道用什么样的算法能够解决什么样的需求，不同的算法怎么去调参、调优

出去面试的时候可能会问一些公式的推导，经常问的都会去推导

复习：

核心：总结了机器学习的套路

1.随机产生w参数
2.把w参数与样本数据带入到误差函数中（最小二重法，损失函数，目标函数，误差函数都是这同一个公式）求解误差值
3.误差值与用户指定的误差阈值比较，
4.如果大于用户指定的误差阈值，继续调整w参数，
（2，3，4）
5.如果误差小于用户指定的误差阈值，那么此时的w参数就是最佳的w参数

问题：
怎么调整w参数？

比如现在w=10 越往大调误差越小，结果往小调就乱调，今天的重点，怎么去调整w参数。

使用一个简单的算法：
梯度下降法：

看图我们知道w1往小调，w0往大调整，但是机器怎么知道，
我们可以把一张图拆成两张图
刚才的w点拆解完之后，w0 和 w1 都是往大调

先验知识：
从凹函数最低点分开，虚线的左半部分导数为负数，导数<0
右半部分导数为正数，导数>0

可以通过导数来指导我们怎么调整w参数
如果 导数<0 ，w参数应该往大调
如果 导数>0 ，w参数应该往小调

现在通过导数可以决定w参数的调整方向，同样道理，再来看这张图，求这个点在w1方向和w0方向上的偏导数。

w0调整就是减去它的导数，当我的导数<0 w应该往大调整
因为导数能指导w参数的调整方向，如果w在虚线的左边，应该往大调整，应该加上一个正数，而此时的导数是负数，w0减去一个负数，就是往大调整
如果w在虚线的右边，w应该往小调整，此时的导数是一个正数，w减去一个正数，就是往小调整。
通过这个公式让我们的导数来决定我们w参数的调整方向。

这个α是学习率，导数是给我们决定w参数调整方向的，调整多大，每次调整的幅度是多少，由α学习率来决定的，就是这个公式。

下面的公式就是对上面公式的导函数的展开，对w0求偏导带入，结果是下面的公式。

就好像我在悬崖上要往山谷里走，走的方向就是导数，走几步路就是α学习率。

结论：
导数的正负，决定了w参数的调整方向，α决定了每次w调整的步长，这个α就是调参工程师需要去调整的，调α是很有学问的。

刚才说的是w0怎么调整，w1也是一样的，求w1的偏导

这是关于上一节课抛出来的问题，w怎么去调整，
现在机器学习的套路需要再细化一下

调整w参数的方法，称之为梯度下降法。
梯度的方向总是正向的，函数变大的方向，我们调整w参数应该沿着它梯度的负方向来调整，所以叫梯度下降法。

----------------------------------用python写一个梯度下降法-------------------------------------

这个代码就是实现了梯度下降法，机器学习的套路：

import numpy as np   # 是python中的一个模块用于做矩阵计算的
import matplotlib.pyplot as plt

# 定义一个函数h(x) 返回 w0 + w1 * x
def h(x):
    return w0 + w1 * x

# main函数
if __name__ == '__main__':
    # α步长
    rate = 10

    # 准备的样本数据 数组,上下对应了看(1,2)(2,3)(3,4)(4,5)(5,6)(6,7)...(9,10)这么9组数据
    # x_train是样本数据的x值
    x_train = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9])
    # y_train是样本数据的y值
    y_train = np.array([2, 3, 4, 5, 6, 7, 8, 9, 10])

    # 随机产生w0
    w0 = np.random.normal()
    # 随机产生w1
    w1 = np.random.normal()
    err = 1


# 能完全等于w0=1 w1=1?

# for循环了10000次  迭代10000次  python不是使用大括号来划分的，是使用缩进来划分的
 for i in range(10000):
# 依据用户指定的误差阈值来收敛
# while err > 0.000000001:
    for x, y in zip(x_train, y_train):
    	# w0 - α * 导数   调整完之后的w0值
        w0 = w0 - rate * (h(x) - y) * 1
        w1 = w1 - rate * (h(x) - y) * x
    # 计算误差值
    err = 0.0
    for x, y in zip(x_train, y_train):
    	# ** 代表平方  h(x) 是带入公式后的y值  这是一条数据的误差，使用err来累加
        err += (y - h(x)) ** 2
    m = len(x_train)
    # 误差函数还要乘 1/2m  m就是样本数据
    err = float(err / (2 * m))
    print("err:%f" % err)

print(w0, w1)

有一点出入：w参数出现之后python代码就对它调整了一把，然后带入到了误差函数中。python是一个解释性语言，按顺序执行，

迭代收敛条件可以由两个，一个用户指定的误差阈值，第二根据用户指定的迭代次数，刚才实现的根据迭代次数来收敛的，也可改成误差阈值
while err>0.00001
依据用户指定的误差阈值来收敛。

给出的数据是在一条直线上的 y=x+1
为什么最后求出来的是一个近似1的值，这是由梯度下降法决定的，因为很难能走到最低谷。不能准确的唯一。因为我们找寻w参数的方式就是这样去找的。

问题：

我可不可以不根据这个公式来调整w参数了。
如果导数>0 应该往小调整，可不可以直接减去学习率
如果导数<0 应该往大调整，可不可以直接加上学习率？

这样不行。
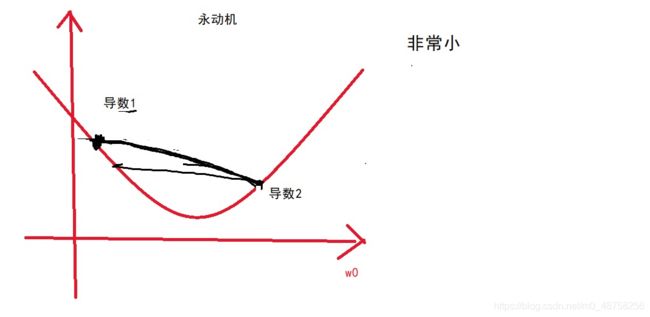
只拿w0来看，假设这个α值设为10
这么大一步可能会跨过来，它现在的导数是大于0的应该往小调整，又减去10，又回来了，来回的震荡，永动机，来回在这两个点震荡。

为什么要加上导数来调整？

导数1的绝对值大于导数2的绝对值
y=x平方 导数 y=2x
越往两边发散，导数越大，x对y的影响越大
往回调的时候一定会比导数1要小，再向前调整一定会比导数2小
来回震荡螺旋下降一直到谷底，这就是在调整w的时候把导数也参与进来。

可不可以把α调的很大，好不好，会有什么后果？
不好！如果这个α调的很大，一步有可能迈到另外一侧，并且纵坐标是要高于原先的，下一步应该往回调整，调回来的纵坐标会比原先同侧位置的点更高，因为这个点的导数是大于原先的点的导数的，α都一样，所以会越来越高，盘旋上升

测试：
在代码中，把rate调整为10，
运行后err非常非常大，比python最大值还要大，并且还报错了

如果α设置的非常巧的话，会在y轴相同的两点间震荡，如果设置的比较小，是震荡下旋，如果设置的大了，会螺旋上升。

关于α的调整是有艺术的，面试官经常问。

以上是解释w参数的调整，为什么遵循这两个公式。

关于损失函数的一个问题：

能不能不用平方，取绝对值？
上节课说平方的目的是防止负数来抵消正数，可不可以加一个绝对值，为什么不用下面的损失函数，而要加一个平方。

平方放大了误差，x越大，对y的影响越大
b越往a移动，对于整体的误差反而在拉大，4个人和2个人拔河比赛，当这个标记离4个人越近的时候，这两个人的爆发力是成二次方的增长，反而这4个人的爆发力并不高。
如果使用第二种损失函数，就很有可能拟合出来a这样一条直线，因为越靠近这4个点，对于整体误差可能是降低的。因为另外两个点的误差不是成平方的放大。

举例：
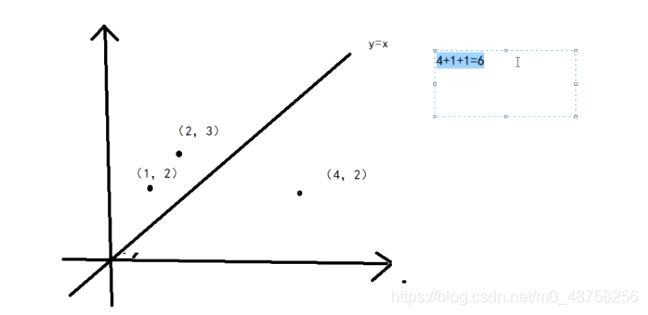
假设一个点坐标(1,2) (2,3) (4,2)
现在有一根直线 y=x
根据第一个误差函数来计算误差值是 4+1+1=6
假设另外一根直线 y=x+1 正好穿过其中的两个点
再计算整体误差，0+0+9=9 整体的误差更大，没移动误差反而小，不会移动

机器学习的目的：
希望空间中的这根直线，距离空间中的点，误差最小，移动完反而增加了，所以不会移动。

使用第一个误差函数，不会完全穿过这两个点，如果使用第二个误差函数
移动前：2+1+1=4
移动后：3+0+0=3
会移动，如果使用这个误差函数，就会从y=x 移动到 y=x+1

最终的目的就是希望，我们拟合出来的这根直线，和我们空间中的点的误差最小，这根直线最完美。找到一个最合适的直线，最能代表空间中数据的规律。

这一切都是在拟合函数。如果现在空间中有这样一些点，假设能找到一根曲线，经过所有的点，问这根曲线好不好？

从误差的角度来看，这个曲线非常厉害，误差完全为0，和空间中的点拟合的非常好。
但依然不好，因为这个曲线，根本代表不了空间中点的规律。当未来x=10, y就不准。这种现象叫做过拟合（拟合过度）。

数据集(x,y)
把所有的数据分为3块 验证集、训练集、测试集
一般在公司里会把 验证集、训练集 占70%到80%
测试集一般占20%到30%左右

分成这3块怎么来控制过拟合，这3块数据都是随机抽出来一部分，训练集和验证集是训练集占90%左右，验证集占10%左右

之前讲的都是通过训练集训练出来一个个的模型，比如这是迭代出来的第一个模型model1，用验证集计算一下在这个model上的误差做一下记录，err1

一个先验的知识：
假设y坐标代表误差，横坐标代表不断迭代出来的model模型，
对于训练集的误差越来越小，
如果它发生了过拟合，由于验证集是不参与训练这个模型的，对于验证集可能在某一个位置会直线飙升（有可能是model发生了过拟合而导致的），接下来会马上发生过拟合，飙升前的这个位置就是最好的model。

接着又迭代出一个模型 model2 再使用验证集来验证它，又计算出来一个 err2
如果 err2 小于 err1 说明还没有发生过拟合。
又迭代出来一个模型 model3 再使用验证集来验证它，又计算出来一个 err3
如果现在的 err3 远远的大于 err2 此时的model3 就可以说可能发生了过拟合。

大多少算过大要看具体的业务场景，如果 err3 比 err2 大的幅度，相比于它们降低的幅度，要多很多，就有可能是发生了过拟合，没法给出一个准确值。

--------------------再来一遍---------------------------

如果可以找到一根曲线，连接图上所有的点，这根曲线从误差的角度来看非常牛逼。但是全盘来看，不好，因为这根曲线没有任何的规律。未来来一个值，它预测的y就不准，如果训练集的误差越来越小，验证集的误差可能在某一个时刻突然飙升，那么飙升的这段，很可能就是由于过拟合而导致的。

所以在训练模型的时候，要使用验证集，不断的来验证这个模型，比如迭代出来的第一个模型，来记录一下验证集的误差，又迭代出来一个，再记录一下，如果现在的err2比err1小，我们说还没有发生过拟合，如果再迭代出来一个，使用验证集来验证记录误差err3，发现err3远远大于err2 有可能发生过拟合。

验证集和测试集的区别：

验证集：辅助训练模型，参与校验模型的
测试集：是来测试model2的，不参与训练模型的环节

问一个问题？
测试集的误差一定大于训练集的误差么？ 不一定。

如果测试集随机抽的数据，完全是训练集的一个子集，他两可以相等，如果测试集的数据和训练集有大部分的交集，可能测试集的误差就大一点点。

--------------------------再梳理一遍-------------------------

机器学习套路里的参数如何去调，应该根据它们的导数去调。
导数只是决定参数调整的方向，具体每天调多少，由α步长来决定
根据学习套路用python来实现了一下
具体去剖析了w调整的公式，如果变成只加减α行不行，一个是永动机原理，一个是螺旋下降
α越大越好还是越小越好？α过大会盘旋上升，正好相等会不断迭代，α较小会螺旋下降，如果非常的小到达谷底的速度会非常的慢。
为什么选择平方的损失函数，不选择绝对值方式的，因为绝对值方式的有可能会把离权值给忽略了，那么在找寻规律的时候，就不是站在一个全局的角度来考虑的，就可以说找出来的规律不准。
都是为了让空间中的这根直线与空间中的点拟合的好，误差要小。
如果过度的拟合反而又不好，因为这根曲线完全没有规律。如果真的能找到这样一根曲线，未来预测的一定不准。怎么控制？使用验证集来辅助选择模型，训练模型。

问题：
如果现在x不是一个是2个，
x1 x2 y
1 1 2
2 2 3
3 3 4
4 4 5
现在的自变量有2个，因变量还是 y
发现一个特点 x1 和 x2 的值一模一样，对于这样一个样本数据
我们要使用 y=w0+w1x1+w2x2 这样一个公式来拟合 需要一个面来拟合它
如果训练集是这个样子，w1 和 w2 是什么关系？
w1=w2