我的西瓜书笔记之“万物基础”——回归

Hello大家好，我是飞燕，目前还是一名在校大学生，对机器学习，深度学习，计算机视觉非常感兴趣。在基本结束了大学本科的数学课程学习之后，开始自学机器学习有关知识，选择了被广泛推荐的《机器学习》（西瓜书）作为入门书籍，在这里把自己学习过程，学习笔记，自认为较为重要的书中的知识点和自己的一些想法写成博客，与大家一起学习讨论，同时也是对自己学习历程的一个记录。这是飞燕第一次写技术性博客，有错误或者不足之处恳请各位批评指出。

《机器学习》笔记——回归

1. 线性回归 (Linear Regression)

  线性回归想必大家都不陌生，早在高中的时候就已经有接触过相关问题。飞燕还记得高中的时候一道线性回归的题值10分，结果算错了就全错了，印象特别深刻。高中的时候老师给出的线性回归表达式有两种：
$$\{\begin{array}{rl}\hat{b}& =\frac{\sum _{i=1}^n(x_i-\overline{x})(y_i-\overline{y})}{\sum _{i=1}^n(x_i-\overline{x}{)}^2}=\frac{\sum _{i=1}^n{x}_i{y}_i-n\overline{x}\overline{y}}{\sum _{i=1}^n{x}_i^2-n{\overline{x}}^2}\\ \hat{a}& =\overline{y}-\hat{b}\overline{x}\end{array}\text{\hspace{1em}(1)}$$
$$y=\hat{b}x+\hat{a}\text{\hspace{1em}(2)}$$
（高中的时候纯手算这个真的是噩梦啊）
这是一维自变量的最小二乘法表示公式，若x为向量$$\mathbf{x}=(x_1,x_2,...,x_n)$$
则(2)式可重写为
$$f(\mathbf{x})=w_1{x}_1+w_2{x}_2+......+w_n{x}_n+b$$
用向量法表示为
$$f(\mathbf{x})={\mathbf{w}}^T\mathbf{x}+b$$
这就是线性回归最终得到的拟合函数表达式。其中我参数b为误差，通常服从正态分布。将其标准化之后可得
$$\frac{b-\mu }{\sigma }\sim N(0,1)$$
运用参数估计中的极大似然估计（MLE）有
$$L(\mathbf{w})=\prod _{i=1}^{n}p(y^{(i)}|x^{(i)};w)=\prod _{i=1}^n\frac{1}{\sqrt{2\pi }}{e}^{-}{\frac{(y^{(i)}-{\mathbf{w}}^T{x}^{(i)})}{2}}^2$$
为了计算方便，我们常常将上述等式取对计算
$$l(\mathbf{w})=n\ln \frac{1}{\sqrt{2\pi }}-\frac{1}{2}\sum _{i=1}^n(y^{(i)}-{\mathbf{w}}^T{x}^{(i)}{)}^2$$
该式中减号之前的部分为常数，接下来计算中可不考虑。故当$l(\mathbf{w})$ 取最大时，只需要对目标函数求最小值即可
$$loss(\widehat{y_i},y_i)=J(\mathbf{w})=\frac{1}{2}\sum _{i=1}^n(y^{(i)}-{\mathbf{w}}^T{x}^{(i)}{)}^2$$
这个式子其实就是今后常常会用到的模型性能度量指标之一——均方误差，通常要使其最小。也可以将上式写为矩阵式：
$${\hat{\mathbf{w}}}^{\ast }=\underset{\hat{\mathbf{w}}}{\mathrm{argmin}}(\mathbf{y}-\hat{\mathbf{w}}\mathbf{X}{)}^T(\mathbf{y}-\hat{\mathbf{w}}\mathbf{X})$$
通过高中知识可知，要求一个函数的最值或极值常用方法为求导，在导函数等于0处的驻点逐一判断是否为最值获极值。
那么我们可以令$f(\hat{\mathbf{w}})=(\mathbf{y}-\hat{\mathbf{w}}\mathbf{X}{)}^T(\mathbf{y}-\hat{\mathbf{w}}\mathbf{X})$,并对$\hat{\mathbf{w}}$求偏导并令其等于0
$$\frac{\partial f}{\partial \hat{\mathbf{w}}}=2{\mathbf{X}}^T(\mathbf{X}\hat{\mathbf{w}}-\mathbf{y})=0$$
若矩阵$({\mathbf{X}\mathbf{X}}^T)$满秩，则上式可解得
$${\hat{\mathbf{w}}}^{\ast }=({\mathbf{X}}^{\mathbf{T}}\mathbf{X}{)}^{-1}{\mathbf{X}}^T\mathbf{y}$$
这也是最小二乘法的矩阵表达形式。
小结：
（1）线性回归的loss函数可以为均方误差，其表达式为
$$loss(\widehat{y_i},y_i)=J(\mathbf{w})=\frac{1}{2}\sum _{i=1}^n(y^{(i)}-{\mathbf{w}}^T{x}^{(i)}{)}^2$$
（2）将均方误差写为矩阵式并对$\hat{\mathbf{w}}$求偏导等于零可以得到最小二乘法的矩阵式
$${\hat{\mathbf{w}}}^{\ast }=({\mathbf{X}}^{\mathbf{T}}\mathbf{X}{)}^{-1}{\mathbf{X}}^T\mathbf{y}$$
将其带入最终的拟合函数表达式可得
$$f({\hat{\mathbf{x}}}_i)={\hat{\mathbf{x}}}_i({\mathbf{X}}^{\mathbf{T}}\mathbf{X}{)}^{-1}{\mathbf{X}}^T\mathbf{y}$$
这就是线性回归最终所学得的模型。
（3）线性回归是最简单的回归形式之一，但其有丰富的变化，并且在处理一些简单的回归问题上可以得到较好的效果。另外，线性回归也是其他很多回归的基础，比如接下来要介绍的Logistic回归。

2. Logistic回归 (Logistic Regression)

   Logistic回归是在线性回归的基础上，将线性回归所得到的结果映射到一个非线性空间当中。为了达成这个目的，我们需要引入一种类似激活函数的东西。在Logistic回归里，这个函数就是大名鼎鼎的Sigmoid函数。
Sigmoid函数表达式为
$$y=\frac{1}{1+e^{-z}}$$
Sigmoid函数图像如下

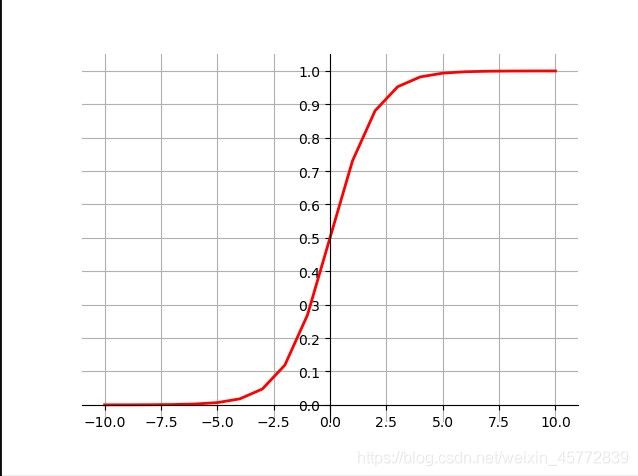
在Sigmoid函数表达式中，y就是我们最后的输出结果，若y为正例的概率，则1-y则为反例概率，二者相比再取对的结果被称为“对数几率”。
$$\ln \frac{y}{1-y}$$
上式与线性回归的结果相结合可有
$$\ln \frac{y}{1-y}={\mathbf{\theta }}^T\mathbf{x}+b$$
该式输出的结果就是”对数几率”，同时也是Logistic回归的输出结果。
那么问题来了，式中参数$\mathbf{\theta }$如何得到呢？其实我们可以照葫芦画瓢，参照线性回归的形式，使用MLE来进行参数估计。
$$L(\mathbf{\theta })=\prod _{i=1}^{n}p(y=1|\mathbf{x}{)}^{y^{(i)}}p(y=0|\mathbf{x}{)}^{(1-y^{(i)})}$$
取对化简有
$$l(\mathbf{\theta })=\sum _{i=1}^n(-y^{(i)}{\mathbf{\theta }}^T\widehat{{\mathbf{x}}_{\mathbf{i}}}+\ln (1+e^{{\mathbf{\theta }}^T\widehat{{\mathbf{x}}_{\mathbf{i}}}}))$$
这就是Logistic回归当$y\in (0,1)$时的目标函数（loss函数），同样，对其求偏导等于0后可以有最终函数的表达式。
如果y为离散型变量，即
$$y=\{\begin{array}{r}-1当x_i为反例\\ 1当x_i为正例\end{array}$$
$$\widehat{y_i}=\{\begin{array}{r}{p}_i{y}_i=1\\ -p_i{y}_i=-1\end{array}$$
令$p_i=\frac{1}{1+e^{-{\mathbf{\theta }}^T{x}_i}}$，同样通过极大似然估计有
$$loss(y_i,\widehat{y_i})=\sum _{i=1}^n\ln (1+e^{-y_i{\mathbf{\theta }}^T{x}_i})$$
小结：
（1）Logistic时以线性回归为基础，将线性回归的结果通过Sigmoid函数映射到非线性空间中的方法。
（2）Logistic回归的目标函数为
$$loss(y_i,\widehat{y_i})=\sum _{i=1}^n(-y^{(i)}{\mathbf{\theta }}^T\widehat{{\mathbf{x}}_{\mathbf{i}}}+\ln (1+e^{{\mathbf{\theta }}^T\widehat{{\mathbf{x}}_{\mathbf{i}}}})$$
（3）Logistic回归常用于分类问题，可以直接对分类可能性建模，不需要实现假设数据分析。同时Logistic回归给出的结果并不是具体的“类别”，而是该样本属于该类别的近似概率。此外，Logistic回归的目标函数具有很好的数学性质，在很多优化算法都可以直接求最优解。

3. 岭回归与LASSO回归 (Ridge Regression and LASSO Regression)

  岭回归与LASSO回归都是再线性回归的基础上加上一个正则项，其目的是为了防止回归模型过拟合。其中LASSO回归加上的是L1正则项(L2-Normalization)，岭回归加上的是L2正则项(L2-Noarmalization)。我们来看看这两个的目标函数。
岭回归：
$$J(\mathbf{\theta })=\frac{1}{2}\sum _{i=1}^n(y^{(i)}-{\mathbf{\theta }}^T{x}^{(i)}{)}^2+\lambda \sum _{j=1}^n{{\mathbf{\theta }}_{\mathbf{j}}}^2$$
LASSO回归：
$$J(\mathbf{\theta })=\frac{1}{2}\sum _{i=1}^n(y^{(i)}-{\mathbf{\theta }}^T{x}^{(i)}{)}^2+\lambda \sum _{j=1}^n|{\mathbf{\theta }}_{\mathbf{j}}|$$
其中$\lambda$表示正则项参与度，是一个超参数，需要用梯度下降等方法调参。关于梯度下降，飞燕将在之后的番外篇里详细讲一下这个东西，因为这个东西真的非常非常重要！
正则化防止过拟合的原因
这里以岭回归为例，为了描述方便，我们将岭回归的目标函数简写为
$$C=C_0+\lambda \sum {\mathbf{\theta }}^2$$
对其求偏导
$$\frac{\partial C}{\partial \theta }=\frac{\partial C_0}{\partial \theta }+2\lambda \sum \mathbf{\theta }$$
我们在使用梯度下降(这里以SGD为例)确定超参数$\lambda$的时候就有
$${\mathbf{\theta }}_{\mathbf{i}}={\mathbf{\theta }}_{\mathbf{i}}-\alpha \frac{\partial C_0}{\partial \theta }-2\alpha \lambda {\mathbf{\theta }}_{\mathbf{i}}=(1-2\lambda ){\mathbf{\theta }}_{\mathbf{i}}-\alpha \frac{\partial C_0}{\partial \theta }$$
其中$\alpha$为学习率。因为$\lambda >0$，所以称上述方法为权重衰减，可以有效减小系数。系数减小了，单个特征影响总体的因素就变小了，最后结果就基本不会出现因为一个特征改变而大幅改变的情况，因此可以有效防止过拟合。

下期预告： 决策树与随机森林

参考文献

• [1] 周志华 《机器学习》
• [2] [中英字幕]吴恩达机器学习系列课程

下期预告： 决策树与随机森林

  好啦以上内容就是本节的主要内容，第一次写技术博客，希望大家多多指教。我是飞燕，我们下期再见~

转载请注明出处