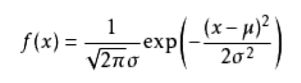R语言绘图及检验——正态分布曲线
正态分布曲线
目录
正态分布曲线
图一
图二
图三
分布检验
如果连续型随机变量X的概率密度函数
具有如下形式：
则称X服从均值为μ，方差为σ^2的正态分布。
图一
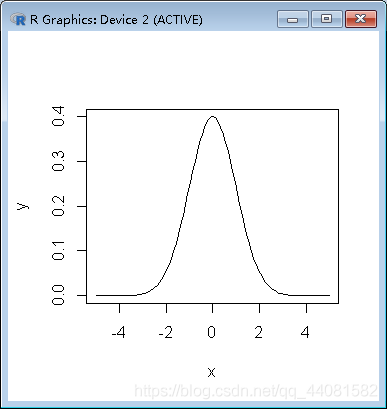
画出在-5-5区间，随机变量X服从N(0,1)的概率密 度函数曲线
知识点说明： dnorm()是正态分布的概率密度函数 rnorm是生成正态分布的随机数 pnorm是分布函数
> x<-seq(-5,5,length.out=100)
> y<-dnorm(x,0,1)
> plot(x,y,type="l")注释：：生成-5到5区间，等间隔距离共100个点，dnorm()是R生成正态分布的概率密度函数，type="l"表示的是划线，最后得到的图形如下：
图二
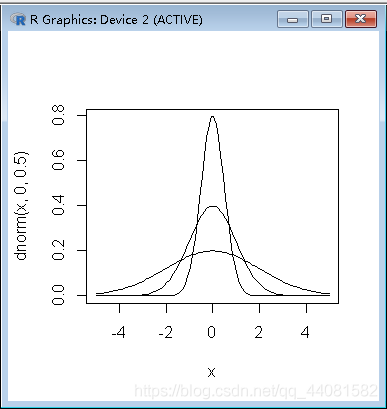
在一幅图中，分别画出在-5,5区间，随机变量服从N（0,0.5）， N（0,1），N（0,2）的概率密度曲线。
> x<-seq(-5,5,length.out=100)
> plot(x,dnorm(x,0,0.5),type="l")
> lines(x,dnorm(x,0,1))
> lines(x,dnorm(x,0,2))
注释：lines是在原图的基础上添加，生成的结果图如下所示：
图三
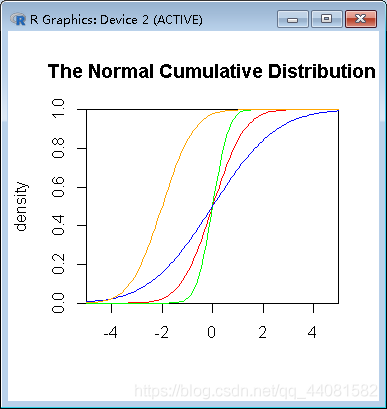
画出随机变量X服从 N（0,0.5），N（0,1）， N（0,2）累计分布曲线。
正态分布的累计分布函数是
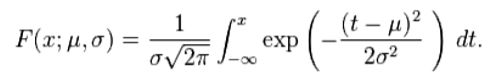
累积分布函数的定义（cumulative distribution function）：对连续函数，所有小于等于a的值，其 出现概率的和。F(a)=P(x<=a)
> x<-seq(-5,5,length.out=100)
> y<-pnorm(x,0,1)
> plot(x,y,col="red",xlim=c(-5,5),ylim=c(0,1),type='l',xaxs="i", yaxs="i",ylab='density',xlab=''
+ , main="The Normal Cumulative Distribution")
> lines(x,pnorm(x,0,0.5),col="green")
> lines(x,pnorm(x,0,2),col="blue")
> lines(x,pnorm(x,-2,1),col="orange")
分布检验
检验随机变量X是否服从正态分布。
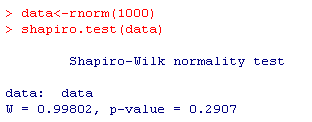
R提供 shapiro.test( )来做检验。用的是ShapiroWilk正态分布检验法，检验样本在3到5000之间。 此方法检验的统计量W：
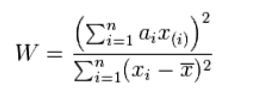
统计量W 最大值是1，越接近1，表示样本与正态分布匹配 p值，如果p-value小于显著性水平α(0.05)，则不满足正态分布。
满足的情况：
不满足的情况：
还可以通过rnorm( )函数模拟一组由1000个数字组成的样本数据，并做分布检验。
通过rnorm()生成的数据样本，肯定是服从正态分布的