深度之眼Paper带读笔记GNN.01.Node2Vec
文章目录
- 前言
-
- 论文结构
- 学习目标
- 论文研究背景、成果、意义
-
- 研究背景
- 研究成果
- 研究意义
- 泛读
-
- 摘要核心观点
- 论文标题
- 传统的图的特征工程
- 图的构建
- 图的应用
- 精读
-
- 论文算法模型总览
- 论文算法模型的细节
-
- 细节一
- 细节二 BFS和DFS
- 细节三 有偏Random Walk算法
- 细节四 算法
- 细节五 alias sampling
- 实验设置和结果分析
- Case Study: Les Misérables network
- Experimental setup
- Multi-label classification
- Parameter sensitivity
- scalibility
- Link prediction
- 论文总结
- 复现
-
- main.py
- node2vec.py
- 问答
前言
本课程来自深度之眼,部分截图来自课程视频。
文章标题:Node2Vec: Scalable Feature Learning for Networks
node2vec:大规模网络节点的表征学习
作者:Adiya Grover,Jure Leskovec(这个是斯坦福讲GML的大佬,战斗民族口音)
单位:Stanford
发表会议及时间:KDD 2016(KDD比较偏实验)
公式输入请参考:在线Latex公式
论文结构
- Abstract:介绍背景及提出node2vec模型,灵活可调的搜索策略。
- Introduction介绍图的重要性、与以前的方法如PCA、ISOMAP、DeepWalk做对比。
- Related Work:传统基于图的人工特征的算法、降维算法等。
- Feature Learning:图的基本概念、skip-gram算法、优化目标函数。
- Search strategies:BFS、DFS、搜索策略。
- Node2vec:Biased random-walk算法、参数p、q的选取方法、时间复杂度分析、
alias sampling。 - Effectiveness:实验探究模型有效性:Case study、baselines参数设定、分类任务和边预测任务。
- Experiments:实验探究鲁棒性、规模化。
- Discussion:总结提出了一种搜索可调的网络表征学习方法并提出进一步研究方向。
学习目标
论文研究背景、成果、意义
研究背景
无处不在的网络(Ubiquitous):计算机、社会科学、生物学、经济学、统计学
图是一种描述复杂数据的模型(任意的节点数量、复杂的关系)vs 图片(CNN)、文本结构(word2vec)

SNAP:Stanford Large Network Dataset Collection
snap数据集是Jure等人不间断收集的网络数据集,极大地推动社交网络领域的发展研究涵盖:节点分类(node classification)、边预测(link prediction)、社群检测(community detection)、网络营销(viral marketing)、网络相似度(network similarity)
Network embedding学习目标:就是将高维的图中节点或者是边降维表示成d维的向量。

研究成果
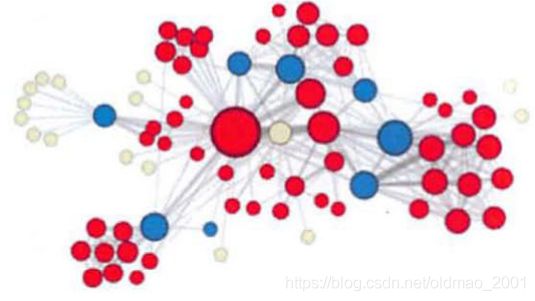
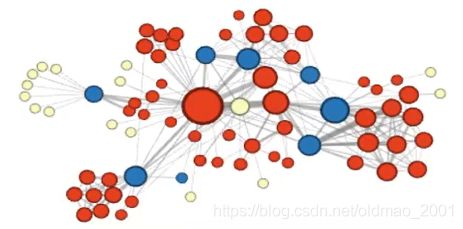
基于Les Miserables数据集的案例分析
数据集规模:n=77,m=254
同质性(社群属性,同一个属性)可视化结果:

结构性(蓝色点在结构上是连接黄色和红色点)可视化结果:
节点分类任务
Macro-F1 vs Micro-F1
Macro-F1:分布计算每个类别的F1,然后做平均
Micro-F1:通过先计算总体的TP,FN和FP的数量,再计算F1
数据集有三个,顶点,边和分类数量如下表:

和基线的对比结果:
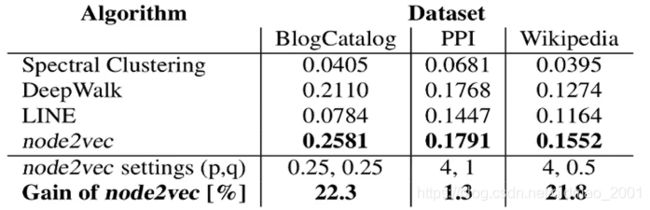
上图中最后一行是性能提升百分比,倒数第二行是Node2Vec取得最佳效果的两个超参数设置。
研究意义
·是Jure目前引用量最高的文章2800+(截止2020.04)
·与DeepWalk[2014]文章一样,属于早期网络表征学习的代表性工作,后期作为经典baseline
·启发了大量基于random walk来做网络表征学习的工作

泛读
摘要核心观点
1.强调之前的基于特征工程的工作的缺点,从而引出node2vec并能探索邻域的多样性
2.通过biased random walk算法提出可调的搜索策略,生成不同语义的节点序列信息
3.讨论算法的高效性、鲁棒性,从案例分析和大量实验论文模型的特点
4.基于以上算法,node2vec算法在多个领域的网络数据集上达到当时的SOTA
论文标题
- Introduction
- Related Work
- Feature Learning Framework
3.1 Classic search strategies
3.2 node2vec
3.3 learning edge features - Experiments
4.1case study
4.2 Experiments setup
4.3 multi-label classification
4.4parameter sensitivity
4.5 Perturbation analysis
4.6Scalability
4.7 link prediction - Discussion and conclusion
传统的图的特征工程
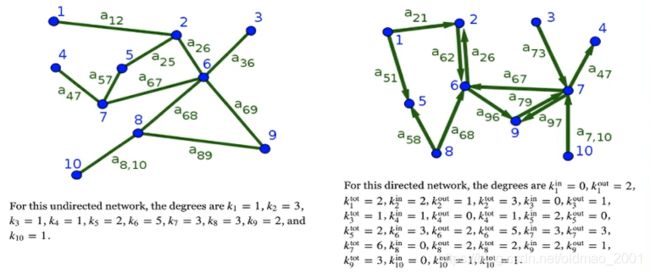
Node centralities
·Degree(in/out):度
·Betweeness:桥
·Closeness:路径长度
·Pagerank:节点重要性
图的构建
1.The fully connected graph
2.The ϵ \epsilon ϵ-neighborhood graph
3.k-nearest neighbor graphs
4.根据实际应用问题建图
5.根据研究问题人工合成图
图的应用
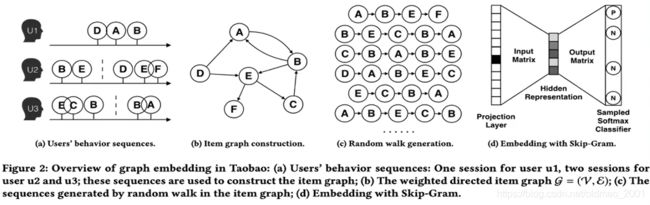
Billion-scale Commodity Embedding for E-commerce Recommendation in Alibaba,
alibaba kdd 2018.
推荐系统:左边的图中虚线代表某个时间段的分割线,横着看是时间序列,用户1先后购买了DAB三个物品,因此在第二个图中DAB三个节点有指向关系,第二个用户购买了BEDEF,由于E和D之间有较长的时间间隔,因此,ED节点之间没有有向边。构造好图结构后,利用DeepWalk或者随机游走产生很多sequence(图c),最后接word2Vec算法,用来做预测。
iFashion:
POG:Personalized Outfit Generation for Fashion Recommendation at Alibaba iFashion, alibaba kdd 2019
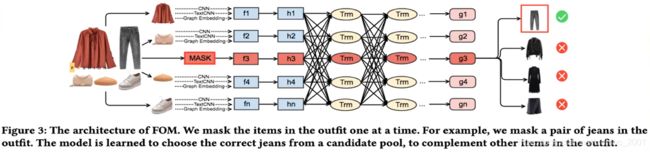
精读
论文算法模型总览
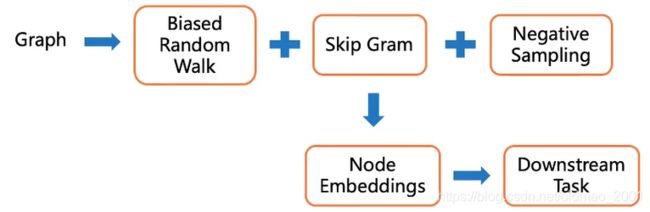
(上图来自百度飞桨课程)
借鉴了Word2Vec算法,引入一个类似的损失函数
分别用DFS和BFS变量图得到的表达所含意义不一样
有偏随机游走算法biased random walk:p和q
图的表示:
Given G = ( V , E ) G=(V,E) G=(V,E), our goal is to learn a mapping
f : u → R d f:u→R^d f:u→Rd
Log-likelihood objective:
max f ∑ u ∈ V logPr ( N S ( u ) ∣ f ( u ) ) (1) \underset{f}{\text{max}}\sum_{u\in V}\text{logPr}(N_S(u)|f(u))\tag1 fmaxu∈V∑logPr(NS(u)∣f(u))(1)
where N S ( u ) N_S(u) NS(u) is neighborhood of node u u u.
Given node u u u, we want to learn feature representations predictive of nodes in its neighborhood N S ( u ) N_S(u) NS(u) .
BFS: Micro-view of neighbourhood
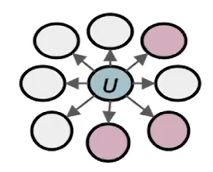
DFS: Macro-view of neighbourhood
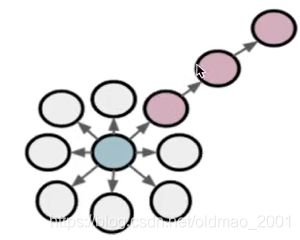
看下半法师和大法师在文中的例子
Two classic strategies to define a neighborhood N S ( u ) N_S(u) NS(u) of a given node u u u (1-hop):

上图中:
N B F S ( u ) = { s 1 , s 2 , s 3 } , Local microscopic view N D F S ( u ) = { s 4 , s 5 , s 6 } , Global macroscopic view N_{BFS(u)}=\{s_1,s_2,s_3\},\text{Local microscopic view}\\ N_{DFS(u)}=\{s_4,s_5,s_6\},\text{Global macroscopic view} NBFS(u)={ s1,s2,s3},Local microscopic viewNDFS(u)={ s4,s5,s6},Global macroscopic view
论文算法模型的细节
细节一
优化目标:类似skip-gram
独立性假设:(Assumption)
邻居节点之间互不影响Conditional likelihood factorizes over the set of neighbors.
负采样
SGD优化方法
论文核心:通过随机游走策略生成 N S ( u ) N_S(u) NS(u)
由于邻居节点之间互不影响的假设,公式(1)可以写成(连乘变连加):
logPr ( N S ( u ) ∣ f ( u ) ) = ∑ n i ∈ N S ( u ) logPr ( f ( n i ) ∣ f ( u ) ) \text{logPr}(N_S(u)|f(u))=\sum_{n_i\in N_S(u)}\text{logPr}(f(n_i)|f(u)) logPr(NS(u)∣f(u))=ni∈NS(u)∑logPr(f(ni)∣f(u))
其中右边就是softmax:
Pr ( f ( n i ) ∣ f ( u ) ) = exp ( f ( n i ) ⋅ f ( u ) ) ∑ v ∈ V exp ( f ( v ) ⋅ f ( u ) ) \text{Pr}(f(n_i)|f(u))=\cfrac{\text{exp}(f(n_i)\cdot f(u))}{\sum_{v\in V}\text{exp}(f(v)\cdot f(u))} Pr(f(ni)∣f(u))=∑v∈Vexp(f(v)⋅f(u))exp(f(ni)⋅f(u))
然后再加上外面的log,公式(1)实际上可以写为(左边是分母,右边是分子,左边忽略一个常数系数):
max f ∑ u ∈ V [ − log Z u + ∑ n i ∈ N S ( u ) f ( n i ) ⋅ f ( u ) ] \underset{f}{\text{max}}\sum_{u\in V}\left [-\text{log}Z_u+\sum_{n_i\in N_{S}(u)}f(n_i)\cdot f(u)\right ] fmaxu∈V∑⎣⎡−logZu+ni∈NS(u)∑f(ni)⋅f(u)⎦⎤
其中
Z u = ∑ v ∈ V exp ( f ( v ) ⋅ f ( u ) ) Z_u=\sum_{v\in V}\text{exp}(f(v)\cdot f(u)) Zu=v∈V∑exp(f(v)⋅f(u))
上式中要对每个顶点来进行计算,实际上计算复杂度还蛮高,论文借鉴了Word2Vec中的负采样和层次softmax来对这项作了优化。
Word2Vec中的负采样是用词频高的作为负样本,这里是用顶点的度当做词频进行负采样。度越高采样概率越大。
细节二 BFS和DFS
BFS算法,用到了数据结构:queue(队列),FIFO(first in first out)先进先出
本文认为BFS:structural equivalence(结构相似性,有相似邻居)
from collections import deque
def iter-bfs(G,s,S=None):
S,Q=set() deque()# Visited-set and queue
Q. append(s)# We plan on visiting s 顶点s是遍历的起始点
while Q:# Planned nodes left?Q队列中放置待访问邻居节点
u=Q.popleft()# Get one
if u in S: continue# Already visited? Skip it #顶点u已访问过跳过
S.add(u)# We' ve visited it now将顶点添加到已访问集合S中
Q.extend(G[u])# Schedule all neighbors G[u]代表顶点u的所有邻居,放到队列中
yield u# Report u as visited,打印顶点
DFS算法,用到了数据结构:stack(栈),先进后出
本文认为DFS:homophily(同质/社群相似性,无论怎么走都在某一个社群中)
def iter_dfs(G,s):
S,Q=set(),[]# Visited-set and queue
Q. append(s)# We plan on visitings
while Q:# Planned nodes left?
u=Q.pop()# Get one 注意这里不是popleft
if u in S: continue #Already visited? Skip it
S.add(u)# We' ve visited it now
Q.extend(G[u])# Schedule all neighbors
yield u # Report u as visited
细节三 有偏Random Walk算法
论文核心:
传统的random walk不具备探索节点不同类型领域的能力,本文认为网络同时具备结构&同质相似性,传统RW的公式为(从节点x跳到v的概率):
P ( c i = x ∣ c i − 1 = v ) = { π v x Z if ( v , x ) ∈ E 0 otherwise P(c_i=x|c_{i-1}=v)=\begin{cases} \cfrac{\pi_{vx}}{Z} & \text{ if } (v,x)\in E \\ 0 & \text{ otherwise } \end{cases} P(ci=x∣ci−1=v)=⎩⎨⎧Zπvx0 if (v,x)∈E otherwise
Z Z Z其实不重要,是所有权重的归一化项。
本文的3.2节是重点,提出了有偏随机游走算法(2nd order):
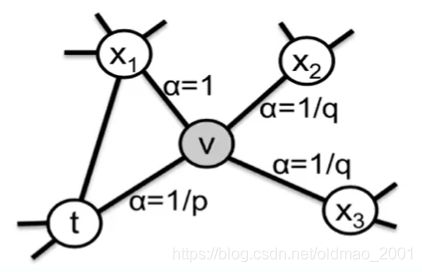
α p q ( t , x ) = { 1 p if d t x = 0 1 if d t x = 1 1 q if d t x = 2 \alpha_{pq}(t,x)=\begin{cases} \cfrac{1}{p} & \text{ if } d_{tx}=0 \\ 1 & \text{ if } d_{tx}=1 \\ \cfrac{1}{q} & \text{ if } d_{tx}=2 \end{cases} αpq(t,x)=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧p11q1 if dtx=0 if dtx=1 if dtx=2
例如:上图中t到t的最短路径是0,因此 α = 1 p \alpha=\cfrac{1}{p} α=p1;
t到x1的最短路径是1,因此 α = 1 \alpha=1 α=1;
t到x2的最短路径是2,因此 α = 1 q \alpha=\cfrac{1}{q} α=q1;
t到x3的最短路径是2,因此 α = 1 q \alpha=\cfrac{1}{q} α=q1;
π v x = α p q ( t , x ) ⋅ w v x \pi_{vx}=\alpha_{pq}(t,x)\cdot w_{vx} πvx=αpq(t,x)⋅wvx
w v x = 1 w_{vx}=1 wvx=1表示无权图
d t x d_{tx} dtx是t,x之间的最短路径(就是当前节点v的一阶邻居节点到节点t的距离),取值范围是0,1,2
当前时间步i在节点v,i-1时间步是在t点,在当前时间步是往哪个节点走是看i-1时间步的,因此叫基于2nd order的有偏随机游走
p和q控制了从源点v离开其他邻居的快慢,是超参数,例如p=1,q=10,权重都为1的情况下,倾向于王x2和x3走,即深度优先。
p:Return parameter
p值大:倾向不回溯,降低了2-hop的冗余度
p值小:倾向回溯,采样序列集中在起始点的周围
q:In-out parameter
q>1:BFS-behavior,local view
q<1:DFS-behavior
细节四 算法
#G = (V, E, W)中W是边的权重
#采样的序列数量为r,序列长度为l
#上下文长度为k
LearnFeatures (Graph G = (V, E, W). Dimensions d, Walks per node r, Walk length l, Context size k, Return p, In-out
q)
π = PreprocessModifiedWeights(G, p, q)
G′ = (V, E, π)
Initialize walks to Empty
for iter = 1 to r do#每个点走r次得到r个序列,把序列添加到walks中
for all nodes u ∈ V do
walk = node2vec Walk(G′, u, l)
Append walk to walks
f = StochasticGradientDescent(k, d walks)
return f#最后学到的函数(network)
node2vecWalk (Graph G′ = (V, E, π), Start node u, Length l)
Inititalize walk to [u]
for walk_iter = 1 to l do
curr = walk[−1]
Vcurr = GetNeighbors(curr, G′)#获得当前节点的所有邻居
s = AliasSample(Vcurr, π)#有偏随机游走中的采样,具体看下面采样技巧
Append s to walk
return walk
细节五 alias sampling
假如有一个事件p有四个状态,发生的概率为:
p = [ 0.3 , 0.2 , 0.1 , 0.4 ] p=[0.3,0.2,0.1,0.4] p=[0.3,0.2,0.1,0.4]
然后逐个累加:
s u m p = [ 0.3 , 0.5 , 0.6 , 1 ] sump=[0.3,0.5,0.6,1] sump=[0.3,0.5,0.6,1]
要检查某个概率对应哪个状态可以用:
逐个查询linear search: O ( n ) O(n) O(n)
由于累加后是递增序列,可以用折半查找binary search: O ( log n ) O(\log n) O(logn)
还有一种更加NB的方法:alias sampling,时间复杂度是 O ( 1 ) O(1) O(1)
大概步骤如下:
有如下四个概率
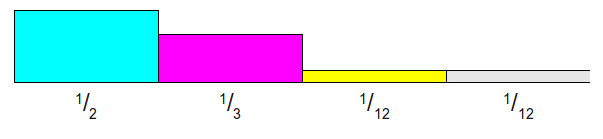
有4个事件的概率,因此把总面积从1变成4,是用他们分别除以1/4(n个事件就除以1/n)
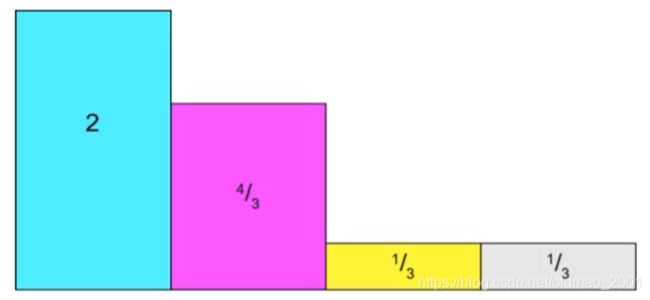
按高度为1进行横切
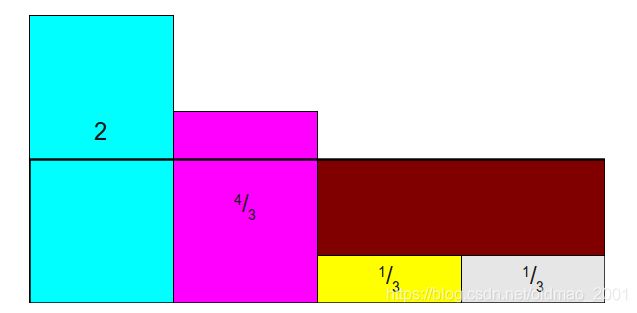
发现右边褐色部分是空缺,需要找多出来的最大的土豪进行重新划分2/3(注意看颜色):
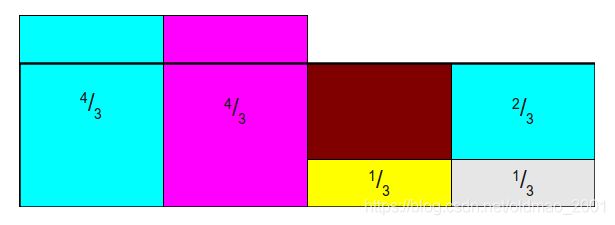
再找一个土豪分2/3,分了以后蓝色又缺了一块:
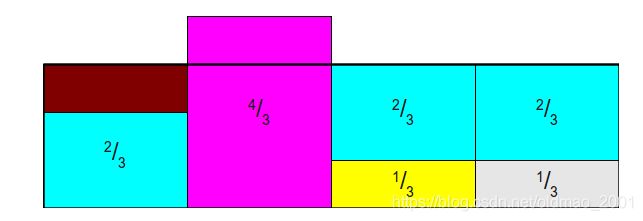
找粉色划分1/3:
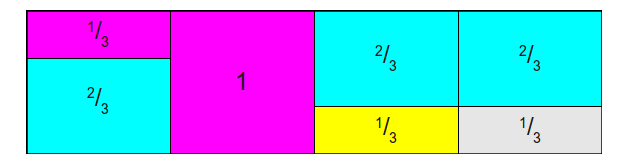
可以看到每一列最多有两个事件,得到下面这个表:

Prob代表是该事件的概率,Alias表示是其他事件的概率,先定位到某一列,然后根据概率值判断是自己还是Alias。
实验设置和结果分析
Case Study: Les Misérables network
数据集:小说数据集,77个节点和254条边,设置的embedding维度d=16,然后用k均值算法进行可视化。
set p = 1, q = 0.5

Experimental setup
然后准备开始做比较试验
下表显示本文有4个baseline:谱聚类(图的拉普拉斯分解),基于DL的有两个
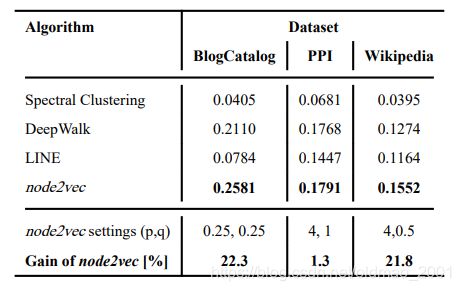
这里要说一下,当p=q=1的时候,就是没有控制随机游走的趋势,是和deepwalk是一样的。
为了公平,与另外两种DL方法使用的训练数据量是一样大小,都是
K = r ⋅ l ⋅ ∣ V ∣ K=r\cdot l\cdot |V| K=r⋅l⋅∣V∣
就是产生的sequence数量(10)乘以sequence长度(80)乘以节点多少是一样的。
都使用SGD作为优化器。
都用负采样。
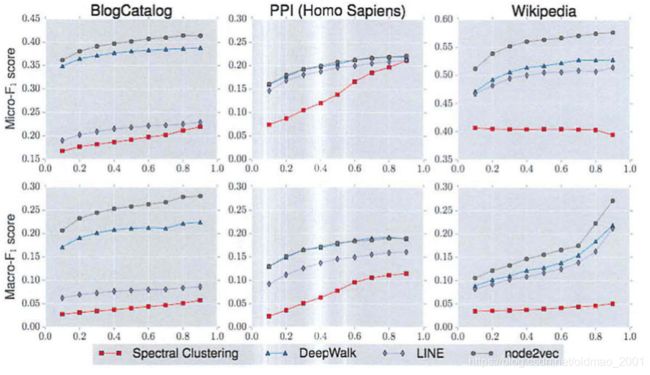
Multi-label classification
有三类数据集:
微博BlogCatalog [38]: This is a network of social relationships of the bloggers listed on the BlogCatalog website. The labels represent blogger interests inferred through the metadata provided by the bloggers. The network has 10,312 nodes, 333,983 edges, and 39 different labels.
蛋白质Protein-Protein Interactions (PPI) [5]: We use a subgraph of the PPI network for Homo Sapiens. The subgraph corresponds to the graph induced by nodes for which we could obtain labels from the hallmark gene sets [19] and represent biological states. The network has 3,890 nodes, 76,584 edges, and 50 different labels.
维基百科Wikipedia [20]: This is a cooccurrence network of words appearing in the first million bytes of the Wikipedia dump. The labels represent the Part-ofSpeech (POS) tags inferred using the Stanford POS-Tagger [32]. The network has 4,777 nodes, 184,812 edges, and 40 different labels.
以上三个数据集都有一个特点,就是既有结构特征,又有社群特征
All these networks exhibit a fair mix of homophilic and structural equivalences.
结果在上面的图中。
Parameter sensitivity
使用不同的数据进行训练在宏观f1和微观f1上得到的结果如下图:
关于参数的敏感度:
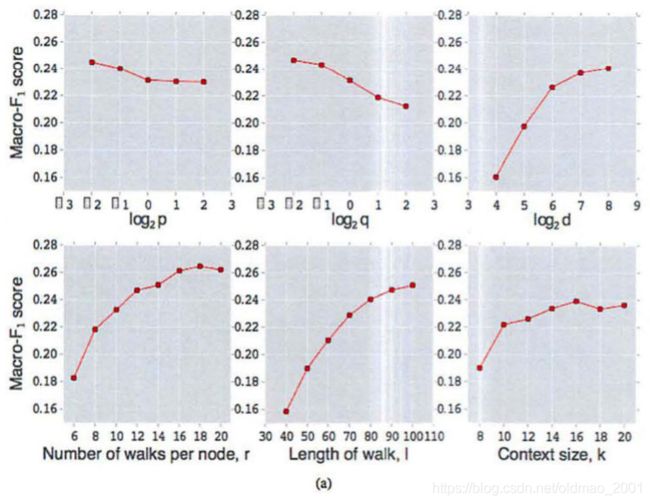
p和q越小,那么回溯和深入游走越细致,效果越好,维度越大也是越好,下面三个图是取的sequence数量,游走的长度,以及上下文的窗口大小,都是越大越好。
scalibility
Link prediction
换了数据集:
Facebook [14]: In the Facebook network, nodes represent users, and edges represent a friendship relation between any two users. The network has 4,039 nodes and 88,234 edges.
Protein-Protein Interactions (PPI) [5]: In the PPI network for Homo Sapiens, nodes represent proteins, and an edge indicates a biological interaction between a pair of proteins. The network has 19,706 nodes and 390,633 edges.
arXiv ASTRO-PH [14]: This is a collaboration network generated from papers submitted to the e-print arXiv where nodes represent scientists, and an edge is present between two scientists if they have collaborated in a paper. The network has 18,722 nodes and 198,110 edges.
结果:

最上面是四个传统算法

Common Neighbors:根据是否有共同的邻居节点来预测是否有边。
Jaccard’s Coefficient:这个在上面的方法上相当做了一个归一化,例如,两个大V,共同好友有1000个,但是各自的好友各有1000万个,两个普通人,共同好友有50个,各自好友约有100个,那么这两个普通人比大V之间可能会认识。
Adamic-Adar Score:在上一个算法基础上考虑朋友的权重。
Preferential Attachment:如果两个用户拥有的好友数量越多,那么就越有可能更愿意去建立联系。也就是“富人越富”原则,基于这思想,用他们两个用户的好友数量的乘积作为评分。
还有一些可以参考:https://blog.csdn.net/a358463121/article/details/79350292
下面的abcd代表四种不同对点和边的处理:
(a) Average, (b) Hadamard, © Weighted-L1, and (d) WeightedL2

其中b的效果最好。
论文总结
关键点
word2vec训练框架
基于random walk产生训练序列
性能–alias sampling
实验设置
创新点
讨论bfs、dfs的语意
设计biased random network
丰富的实验论证效果
启发点
图的理解对网络表征学习的作用(必看)
本文的作者是图/社交网络方向的研究者,其切入的视角是对图的理解
基于random walk方法启发了大量的工作
从2014年的random-walk,2016年的node2vec(本文),直至2020年都还有大量工作metapath2vec:Scalable Representation Learning for Heterogeneous Networks[kdd17]
复杂度分析
算法部分细致的讨论,展示了算法的高效性
复现
karate数据集,可以在 https://github.com/aditya-grover/node2vec/ 上下载
34个点
主要是alias table的代码实现,注意对应上面的伪代码
main.py
'''
Reference implementation of node2vec.
Author: Aditya Grover
For more details, refer to the paper:
node2vec: Scalable Feature Learning for Networks
Aditya Grover and Jure Leskovec
Knowledge Discovery and Data Mining (KDD), 2016
'''
import argparse
import numpy as np
import networkx as nx
import node2vec
from gensim.models import Word2Vec
# 读图,设置模型参数
# 计算点和边的alias table
# 有偏的随机游走生成节点序列
# 利用word2vec训练模型
# 结果展示和可视化
# 1.读图,设置模型参数
# 1)设置模型参数:设置图相关参数,如有向无向图、权重图等,还有模型系数,如p、q、embedding长度等
# 2)读图读图的方式很简单,使用networx包直接加载edgelist
# 3)输入输出
# 输入文件../graph/karate.edgelist'
# 输出文件../emb/karate.emtb'
def parse_args():
'''
Parses the node2vec arguments.
'''
parser = argparse.ArgumentParser(description="Run node2vec.")
# 输入文件
parser.add_argument('--input', nargs='?', default='graph/karate.edgelist', help='Input graph path')
# 输出文件
parser.add_argument('--output', nargs='?', default='emb/karate.emb', help='Embeddings path')
# 表征维度
parser.add_argument('--dimensions', type=int, default=128, help='Number of dimensions. Default is 128.')
# sequence长度
parser.add_argument('--walk-length', type=int, default=80, help='Length of walk per source. Default is 80.')
# 每个节点生成sequence的次数
parser.add_argument('--num-walks', type=int, default=10, help='Number of walks per source. Default is 10.')
# skip-gram上下文窗口大小
parser.add_argument('--window-size', type=int, default=10, help='Context size for optimization. Default is 10.')
parser.add_argument('--iter', default=1, type=int, help='Number of epochs in SGD')
parser.add_argument('--workers', type=int, default=8, help='Number of parallel workers. Default is 8.')
parser.add_argument('--p', type=float, default=1, help='Return hyperparameter. Default is 1.')
parser.add_argument('--q', type=float, default=1, help='Inout hyperparameter. Default is 1.')
parser.add_argument('--weighted', dest='weighted', action='store_true',
help='Boolean specifying (un)weighted. Default is unweighted.')
parser.add_argument('--unweighted', dest='unweighted', action='store_false')
parser.set_defaults(weighted=False)
parser.add_argument('--directed', dest='directed', action='store_true',
help='Graph is (un)directed. Default is undirected.')
parser.add_argument('--undirected', dest='undirected', action='store_false')
parser.set_defaults(directed=False)
return parser.parse_args()
def read_graph():
'''
Reads the input network in networkx.
'''
if args.weighted:#有向有权图设置不同权重
G = nx.read_edgelist(args.input, nodetype=int, data=(('weight', float),), create_using=nx.DiGraph())
else:#有向无权图设置权重都为1
G = nx.read_edgelist(args.input, nodetype=int, create_using=nx.DiGraph())
for edge in G.edges():
G[edge[0]][edge[1]]['weight'] = 1
if not args.directed:#无向图
G = G.to_undirected()
return G
def learn_embeddings(walks):
'''
Learn embeddings by optimizing the Skipgram objective using SGD.
'''
#这句是把int转换为string,但是python2的
#walks = [map(str, walk) for walk in walks]
#改写为python3的
walk_new = []
for walk in walks:
tmp = []
for node in walk:
tmp.append(str(node))
walk_new.append(tmp)
model = Word2Vec(walk_new, size=args.dimensions, window=args.window_size, min_count=0, sg=1, workers=args.workers,
iter=args.iter)
model.save_word2vec_format(args.output)
return
def main(args):
'''
Pipeline for representational learning for all nodes in a graph.
'''
nx_G = read_graph()
G = node2vec.Graph(nx_G, args.directed, args.p, args.q)
G.preprocess_transition_probs()#生成aliastable
walks = G.simulate_walks(args.num_walks, args.walk_length)# 有偏的随机游走生成节点序列
learn_embeddings(walks)
if __name__ == "__main__":
args = parse_args()
main(args)
node2vec.py
import numpy as np
import networkx as nx
import random
class Graph():
def __init__(self, nx_G, is_directed, p, q):
self.G = nx_G
self.is_directed = is_directed
self.p = p
self.q = q
def node2vec_walk(self, walk_length, start_node):#核心算法,如何产生单点有偏的随机游走序列
'''
Simulate a random walk starting from start node.
'''
G = self.G
alias_nodes = self.alias_nodes
alias_edges = self.alias_edges
walk = [start_node]
while len(walk) < walk_length:# 循环到sequence的长度为止
cur = walk[-1]
cur_nbrs = sorted(G.neighbors(cur))#这里排序目的是要和aliastable计算顺序对应
if len(cur_nbrs) > 0:
if len(walk) == 1:#sequence只有一个节点的情况就不跳转别的节点
walk.append(cur_nbrs[alias_draw(alias_nodes[cur][0], alias_nodes[cur][1])])
else:
prev = walk[-2]#前一个节点
#下一个节点
next = cur_nbrs[alias_draw(alias_edges[(prev, cur)][0],
alias_edges[(prev, cur)][1])]
walk.append(next)
else:
break
return walk
def simulate_walks(self, num_walks, walk_length):#循环迭代单点游走函数
'''
Repeatedly simulate random walks from each node.
'''
G = self.G
walks = []#列表
nodes = list(G.nodes())
print 'Walk iteration:'
for walk_iter in range(num_walks):#每个节点走num_walks次
print str(walk_iter+1), '/', str(num_walks)
random.shuffle(nodes)# 打乱节点的顺序
for node in nodes:
walks.append(self.node2vec_walk(walk_length=walk_length, start_node=node))
return walks
def get_alias_edge(self, src, dst):
'''
Get the alias edge setup lists for a given edge.
'''
G = self.G
p = self.p
q = self.q
unnormalized_probs = []
for dst_nbr in sorted(G.neighbors(dst)):#跳转核心算法,和p,q有关,p是回溯,q是下一个邻居
# 通过pq计算下一条的权重
if dst_nbr == src:
unnormalized_probs.append(G[dst][dst_nbr]['weight']/p)
elif G.has_edge(dst_nbr, src):
unnormalized_probs.append(G[dst][dst_nbr]['weight'])
else:
unnormalized_probs.append(G[dst][dst_nbr]['weight']/q)
# 归一化
norm_const = sum(unnormalized_probs)
normalized_probs = [float(u_prob)/norm_const for u_prob in unnormalized_probs]
return alias_setup(normalized_probs)
def preprocess_transition_probs(self):
'''
Preprocessing of transition probabilities for guiding the random walks.
'''
G = self.G
is_directed = self.is_directed#是否有向图
alias_nodes = {
}#创建词典
for node in G.nodes():#对图上每个节点做循环
unnormalized_probs = [G[node][nbr]['weight'] for nbr in sorted(G.neighbors(node))]#找到每个节点的邻居,例如找到4个
norm_const = sum(unnormalized_probs)#求和1+1+1+1=4(这里是无权图)
normalized_probs = [float(u_prob)/norm_const for u_prob in unnormalized_probs]#然后得到跳转到邻居的概率是1/4,注意如果是这样等概率情况,在aliastable中永远是取自己,不取替身。
alias_nodes[node] = alias_setup(normalized_probs)#将跳转概率使用aliastable算法采样,得到O(1)的复杂度
alias_edges = {
}
triads = {
}
if is_directed:
for edge in G.edges():#对边也做在aliastable操作
alias_edges[edge] = self.get_alias_edge(edge[0], edge[1])
else:
for edge in G.edges():
alias_edges[edge] = self.get_alias_edge(edge[0], edge[1])
alias_edges[(edge[1], edge[0])] = self.get_alias_edge(edge[1], edge[0])
self.alias_nodes = alias_nodes
self.alias_edges = alias_edges
return
def alias_setup(probs):
'''
Compute utility lists for non-uniform sampling from discrete distributions.
Refer to https://hips.seas.harvard.edu/blog/2013/03/03/the-alias-method-efficient-sampling-with-many-discrete-outcomes/
for details
'''
K = len(probs)
q = np.zeros(K)#概率
J = np.zeros(K, dtype=np.int)#替身
smaller = []
larger = []
for kk, prob in enumerate(probs):#将概率分为两种,大于1和小于1的
q[kk] = K*prob
if q[kk] < 1.0:
smaller.append(kk)
else:
larger.append(kk)
# 使用贪心算法,将概率小于1的不断填满。对应算法第三步
while len(smaller) > 0 and len(larger) > 0:
small = smaller.pop()
large = larger.pop()
J[small] = large
q[large] = q[large] + q[small] - 1.0
if q[large] < 1.0:
smaller.append(large)
else:
larger.append(large)
return J, q
def alias_draw(J, q):#具体采样算法,O(1)
'''
Draw sample from a non-uniform discrete distribution using alias sampling.
'''
K = len(J)
kk = int(np.floor(np.random.rand()*K))
if np.random.rand() < q[kk]:
return kk
else:
return J[kk]
问答
这里记录一些同学的问题和回答。
为什么每次聚类后的结果差异特别大?
单就聚类算法来说,聚类本来就是一种无监督学习,同样的数据和类别数,每一次聚类执行,因为没有固定的监督label,每一次算法对于聚类中心的选择就带有随机性,不是固定的,所以聚类结果也都是有差异的,这是正常的,跟分多少类没有直接关系。然后整个训练或推理结果,要结合网络其他计算方式一起分析。By Ariel