深度学习-初识Tensorflow框架、Keras框架(中篇笔记)
欢迎大家访问我的个人主页:https://yunfanzhilu.github.io/
以下为读书笔记
摘要
这篇文章是深度学习-初识TensorFlow框架、Keras框架中篇内容,这文章中我将继续以MNIST为例,建立多层卷积网络(大体就是三层:卷积层、池化层、全连接层)来进行识别,此方法可以将识别率提升至98%左右。
卷积(Convolution)
概念
卷积是深度学习一个重要的概念,个人觉得用一句话描述最恰当:“卷积就是两个事物关系的大小”
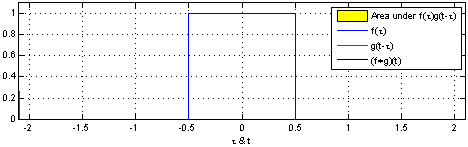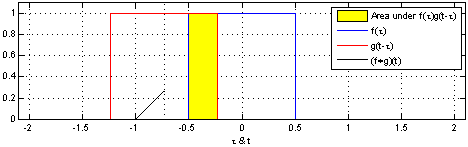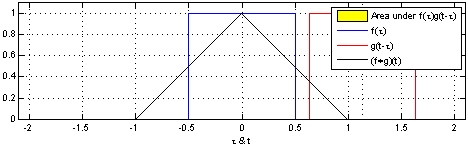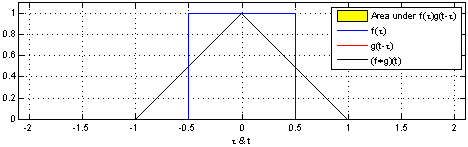
我们先来看一张动图
可以看到三角形的值就是两个矩形“擦肩而过”的值的大小,当两个矩形完全重合(两个关系最大)时卷积的值也最大。
再来看一张动图
左边可以看成一张图像,其中每个值代表有无像素(灰色图像),黄色运动的方框我们称之为卷积核(Convolution Kernel),它不断移动计算卷积的大小,右边是算出的卷积特征值(Convolved Feature)。
卷积的好处
这样做有两个好处:
- image图片的特征值集中被表现出来。
- 右边的矩阵明显更小了,有利于CPU、GPU的运算。
之前在人工智能、机器学习、深度学习概述这篇文章,讲明了深度学习就是把底层特征抽象成高级特征再抽象成为物体并识别出来的原则(有点类似“点、线、面、体”的概念,就是层层抽象,维度增加),这么卷积在其中就扮演了“搬运工”的重要角色。
试想世间万物都是可以从最简单的点抽象成简单的直线段、弯线段再抽象成长方体、正方体,再抽象成汽车、大象等等,如果我们设置合理数量的卷积神经网络层数(层数就等于我们做一次整体卷积运算的次数),就能识别出这个具体的物体,事实证明,用这种方法得出的模型有着更好的效果,识别准确率比普通的线性层回归准确率要高。
卷积神经网络(CNN)比上篇的线性层回归要好?
从识别结果准确率来看:是的!
个人觉得卷积神经网络层之所以准确率高,是因为它让图像中每一个点去指导后面的点,让每个图像的每个点都产生关系,一些不平整的点更像是一条曲线,而不像一条直线,之后一条曲线,更像是一个女生的身材,而不像一个男生的身材。
对比上篇中的线性层回归单纯是每个点,这个点的像素意味着什么,跟这个点后面像素是什么值没啥关系,就像这个像素点是红色,我们认为红色汽车图片在这个点更有可能是红色,因此会给这个点一个正权值,下一个像素点是蓝色,我们认为红色汽车图片在这个点不太可能出现蓝色,因此会给这个点一个负权值,之后就把所有点的权值乘积相加判断,这样就明显没有卷积的方法好。
池化(Pooling)
概念
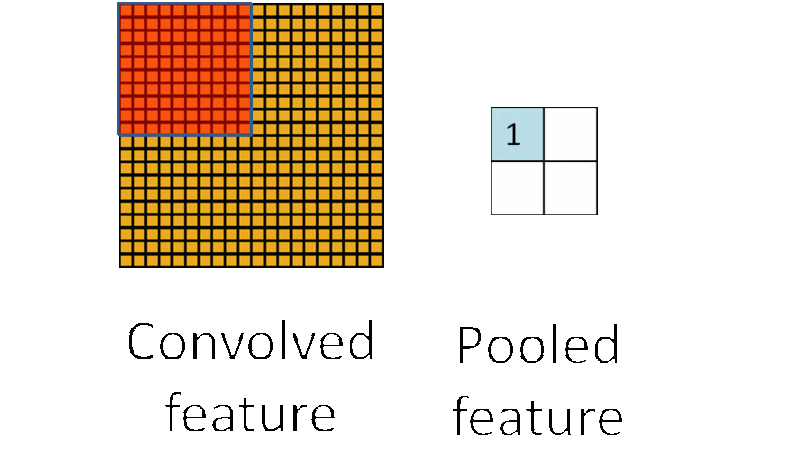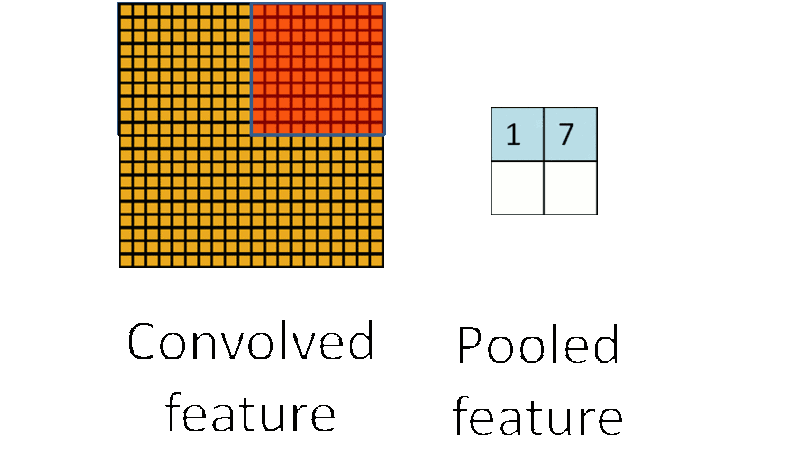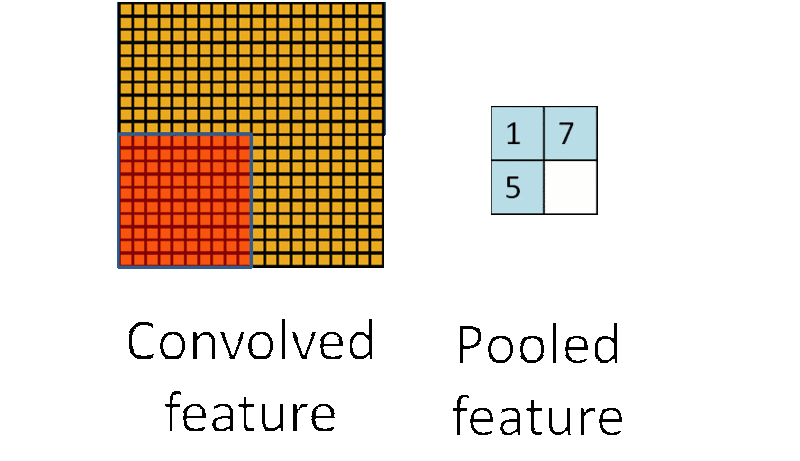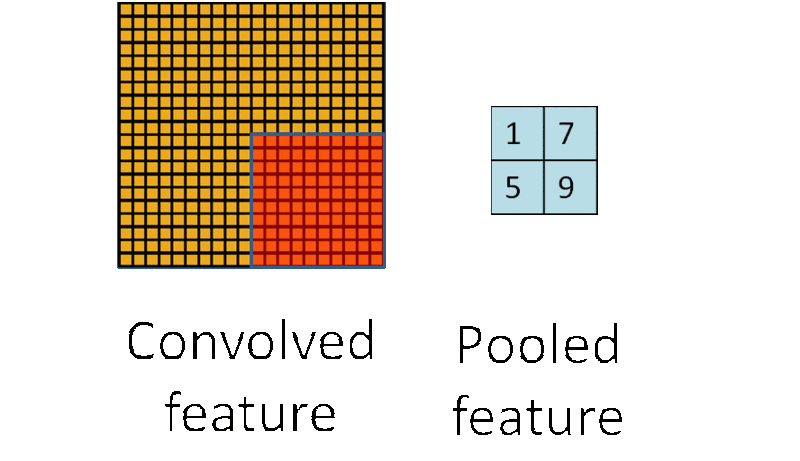
我们还是来看一张动图
看出来了吗?池化就是采样(sample),把算出来的卷积结果再一次采样,进一步缩小图片的大小(因为好算嘛)。
分类
在实际应用中,池化根据下采样的方法,分为
- 最大值下采样(Max-Pooling):一般是在池化核对应区域内选取最大值来表征该区域。
- 平均值下采样(Mean-Pooling): 一般是取池化核对应区域内所有元素的均值来表征该区域。
代码(来自TensorFlow中文社区)
# -*- coding: utf-8 -*-
"""
Created on Wed May 22 17:01:29 2019
@author: Tony
"""
import tensorflow as tf
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)
sess=tf.InteractiveSession()
#权重初始化
def weight_variable(shape):
initial=tf.truncated_normal(shape,stddev=0.1)
return tf.Variable(initial)
def bias_variable(shape):
initial=tf.constant(0.1,shape=shape)
return tf.Variable(initial)
#卷积与池化
def conv2d(x, W):
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],
strides=[1, 2, 2, 1], padding='SAME')
#第一层卷积
W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])
x_image = tf.reshape(x, [-1,28,28,1])
h_conv1=tf.nn.relu(conv2d(x_image,W_conv1)+b_conv1)
h_pool1 = max_pool_2x2(h_conv1)
#第二层卷积层
W_conv2=weight_variable([5,5,32,64])
b_conv2=bias_variable([64])
h_conv2=tf.nn.relu(conv2d(h_pool1,W_conv2)+b_conv2)
h_pool2 = max_pool_2x2(h_conv2)
#密集连接层
W_fc1=weight_variable([7*7*64,1024])
b_fc1=bias_variable([1024])
h_pool2_flat=tf.reshape(h_pool2,[-1,7*7*64])
h_fc1= tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
#Dropout
keep_prob = tf.placeholder("float")
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)
#输出层
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
y_conv=tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)
cross_entropy = -tf.reduce_sum(y_*tf.log(y_conv))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(y_conv,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
sess.run(tf.initialize_all_variables())
for i in range(700):
batch = mnist.train.next_batch(50)
if i%100 == 0:
train_accuracy = accuracy.eval(feed_dict={
x:batch[0], y_: batch[1], keep_prob: 1.0})
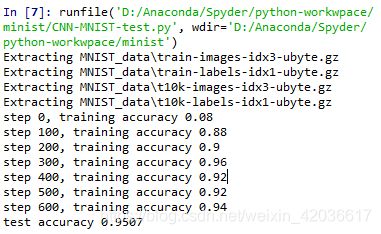
print ("step %d, training accuracy %g"%(i, train_accuracy))
train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})
print("test accuracy %g"%accuracy.eval(feed_dict={
x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1.0}))
代码运行注意其中有很多参数都基于线性层回归上篇的内容,因此你要先运行上篇中的代码把y_、x之类的参数保存下来再运行这个代码才能出结果。
我们可以看到这样准确率比较高,这个就是卷积网络的优势,接下来我们来具体分析一下代码。
各种层分析
卷积层与池化层
第一层卷积
为了用这一层,我们要先处理一下图片
x_image = tf.reshape(x, [-1,28,28,1])
第2、第3维对应图片的宽、高,1代表通道数,灰度图通道数就是1,彩色图(RGB)通道数就是3,第一维-1这个第一维的-1是指我们可以先不指定。
输入层这个tensor的大小为28×28×1
W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])
第一句意思是设置32个5*5的卷积核,这样可以学习32个特征(这里32你可以随意设置,就是指卷积核的数量,设置越多,学习目标特征就越多,理论上识别率就越高),第三维是输入的通道数目,第四维是输出的通道数目。
第二句意思是在每一个输出通道加一个偏置量(Offset)b,还记得那个公式吗?
y = s o f t m a x ( W x + b ) y=softmax(Wx+b) y=softmax(Wx+b)
其中括号部分又可以写成:
e v i d e n c e i = ∑ j W i , j x j + b i evidence_i=\sum_j{W_{i,j}x_j+b_i} evidencei=j∑Wi,jxj+bi
第一层卷积这个tensor的shape大小为28×28×32
因此下一步就要进行x_image和权值向量的卷积啦
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
第一句x_image和权值向量进行卷积,对应于上方evidence公式。
注意这里是卷积,公式上是乘法,这就是CNN对比线性层回归的优势所在,卷积更能体现目标特征值,优化训练数据。
解释一波ReLU激活函数:全称修正线性单元(Rectified linear unit,ReLu),个人理解简单来说就是:**保留evidence中有用的目标特征值,更好的挖掘相关特征,拟合训练数据。**详情参考:ReLU激活函数:简单之美
第一层池化
h_pool1 = max_pool_2x2(h_conv1)
意思是最大值下采样(池化),现在shape大小为14×14×32。
第二层卷积
通常为了更好地识别效果,我们会设置多层卷积神经网络,根据Hebb学习规则,某种特征训练的次数越多,在以后的识别过程中就越容易被检测。
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
第二层中,设置64个5x5的卷积核,学习64个特征,之后进行卷积,与第一层操作一样。
第二层卷积这个tensor的shape:14×14×64
第二层池化
h_pool2 = max_pool_2x2(h_conv2)
意思是最大值下采样(池化),现在这个tensor的shape大小为7×7×64
密集连接层(全连接层)
先上代码:
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
现在我们要把7×7×64这个tensor连接到一块,我们把池化层输出的张量reshape成一些向量,乘上权重矩阵,加上偏置,然后对其使用ReLU。现在这个tensor的shape大小为1×1024
Dropout
keep_prob = tf.placeholder("float")
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)
为了减少过拟合用的,我们用一个placeholder来代表一个神经元的输出在dropout中保持不变的概率。这样我们可以在训练过程中启用dropout,在测试过程中关闭dropout。 TensorFlow的tf.nn.dropout操作除了可以屏蔽神经元的输出外,还会自动处理神经元输出值的scale。所以用dropout的时候可以不用考虑scale。
关于过拟合,请参考Andrew Ng公开课:欠拟合与过拟合的概念
softmax层
之前我们说过,softmax模型可以用来给不同的对象分配概率,不仅在上篇中线性层回归中我们用softmax回归判断概率,而且在之后更加精细的模型中,最后一步也需要用softmax来分配概率。
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
y_conv=tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)
我们设置一个softmax层,把向量化后的图片x和权重矩阵W相乘,加上偏置b,然后计算每个分类的softmax概率值。这样得到这个tensor的shape大小为10,分别代表数字0~9,选择其中概率最大的一个数字就是结果。
训练和评估模型
我们使用与之前简单的单层SoftMax神经网络模型几乎相同的一套代码,只是我们会用更加复杂的ADAM优化器来做梯度最速下降,在feed_dict中加入额外的参数keep_prob来控制dropout比例。然后每100次迭代输出一次日志。
cross_entropy = -tf.reduce_sum(y_*tf.log(y_conv))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(y_conv,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
sess.run(tf.initialize_all_variables())
for i in range(20000):
batch = mnist.train.next_batch(50)
if i%100 == 0:
train_accuracy = accuracy.eval(feed_dict={
x:batch[0], y_: batch[1], keep_prob: 1.0})
print "step %d, training accuracy %g"%(i, train_accuracy)
train_step.run(feed_dict={
x: batch[0], y_: batch[1], keep_prob: 0.5})
print "test accuracy %g"%accuracy.eval(feed_dict={
x: mnist.test.images, y_: mnist.test.labels, keep_prob: 1.0})
参考链接:
卷积神经网络(https://xudonghecs.github.io/2018/12/23/卷积神经网络/#more)
深度学习简介(一)——卷积神经网络(https://www.cnblogs.com/alexcai/p/5506806.html)
TensorFlow中文社区(http://www.tensorfly.cn/tfdoc/tutorials/mnist_pros.html)
ReLU激活函数:简单之美(https://blog.csdn.net/cherrylvlei/article/details/53149381)
深入学习卷积神经网络中卷积层和池化层的意义(https://www.cnblogs.com/wj-1314/p/9593364.html)
Tensorflow- 卷积网络的MNIST源码详尽解析(https://www.jianshu.com/p/fabf52b35a08)