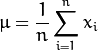OpenCV 人脸识别 EigenFace —— PCA的应用

尊重原创者，转载自：http://www.cnblogs.com/mikewolf2002/p/3432243.html

                            http://www.cnblogs.com/mikewolf2002/p/3432270.html

• 一、   OpenCV中应用PCA生成特征脸

    对一副宽p、高q的二维灰度图，要完整表示该图像，需要m = p*q维的向量空间，比如100*100的灰度图像，它的向量空间为100*100=10000。下图是一个3*3的灰度图和表示它的向量表示：

该向量为行向量，共9维，用变量表示就是[v0, v1, v2, v3, v4, v5, v6, v7, v8]，其中v0...v8，的范围都是0-255。

      现在的问题是假如我们用1*10000向量，表示100*100的灰度图，是否向量中的10000维对我们同样重要？肯定不是这样的，有些维的值可能对图像更有用，有些维相对来说作用小些。为了节省存储空间，我们需要对10000维的数据进行降维操作，这时就用到了PCA算法，该算法主要就是用来处理降维的，降维后会尽量保留更有意义的维数，它的思想就是对于高维的数据集来说，一部分维数表示大部分有意义的数据。

算法的基本原理：

假设   表示一个特征向量，其中 【注：xi可能也是一个列向量】

1.计算均值向量 

2.计算协方差矩阵 S

3.计算S的特征值   和对应的特征向量，根据线性代数知识我们知道有公式：

4. 对特征值按照大小进行递减排序，特征向量的顺序和特征值是一致的。假设我们只需要保留K个维数(K

对于被观测的向量，它的K个主成分量可以通过下面公式计算得到：

，其中

因为W是正交矩阵，所有有。

下面我们在OpenCV中看一个计算PCA的例子：

1.首先读入10副人脸图像，这些图像大小相等，是一个人的各种表情图片。

2.把图片转为1*pq的一维形式，p是图像宽，q是图像高。这时我们的S矩阵就是10行，每行是pq维的向量。

3.然后我们在S上执行PCA算法，设置K=5，求得5个特征向量，这5个特征向量就是我们求得的特征脸，用这5个特征脸图像，可以近似表示之前的十副图像。

图像库下载链接：http://www.cl.cam.ac.uk/Research/DTG/attarchive:pub/data/att_faces.zip

#include "opencv2/core/core.hpp"
#include "opencv2/highgui/highgui.hpp"
#include "opencv2/contrib/contrib.hpp"

#include 
#include 
#include 

using namespace cv;
using namespace std;




//把图像归一化为0-255，便于显示
Mat norm_0_255(const Mat& src)
    {
    Mat dst;
    switch(src.channels())
        {
    case 1:
        cv::normalize(src, dst, 0, 255, NORM_MINMAX, CV_8UC1);
        break;
    case 3:
        cv::normalize(src, dst, 0, 255, NORM_MINMAX, CV_8UC3);
        break;
    default:
        src.copyTo(dst);
        break;
        }
    return dst;
    }

//转化给定的图像为行矩阵
Mat asRowMatrix(const vector& src, int rtype, double alpha = 1, double beta = 0)
    {
    //样本数量
    size_t n = src.size();
    //如果没有样本，返回空矩阵
    if(n == 0)
        return Mat();
    //样本的维数
    size_t d = src[0].total();

    Mat data(n, d, rtype);
    //拷贝数据
    for(int i = 0; i < n; i++)
        {

        if(src[i].empty()) 
            {
            string error_message = format("Image number %d was empty, please check your input data.", i);
            CV_Error(CV_StsBadArg, error_message);
            }
        // 确保数据能被reshape
        if(src[i].total() != d) 
            {
            string error_message = format("Wrong number of elements in matrix #%d! Expected %d was %d.", i, d, src[i].total());
            CV_Error(CV_StsBadArg, error_message);
            }
        Mat xi = data.row(i);
        //转化为1行，n列的格式
        if(src[i].isContinuous())
            {
            src[i].reshape(1, 1).convertTo(xi, rtype, alpha, beta);
            } else {
                src[i].clone().reshape(1, 1).convertTo(xi, rtype, alpha, beta);
            }
        }
    return data;
    }

int main(int argc, const char *argv[])
    {

    vector db;

    string prefix = "../att_faces/";

    db.push_back(imread(prefix + "s1/1.pgm", IMREAD_GRAYSCALE));
    db.push_back(imread(prefix + "s1/2.pgm", IMREAD_GRAYSCALE));
    db.push_back(imread(prefix + "s1/3.pgm", IMREAD_GRAYSCALE));
    db.push_back(imread(prefix + "s1/4.pgm", IMREAD_GRAYSCALE));
    db.push_back(imread(prefix + "s1/5.pgm", IMREAD_GRAYSCALE));
    db.push_back(imread(prefix + "s1/6.pgm", IMREAD_GRAYSCALE));
    db.push_back(imread(prefix + "s1/7.pgm", IMREAD_GRAYSCALE));
    db.push_back(imread(prefix + "s1/8.pgm", IMREAD_GRAYSCALE));
    db.push_back(imread(prefix + "s1/9.pgm", IMREAD_GRAYSCALE));
    db.push_back(imread(prefix + "s1/10.pgm", IMREAD_GRAYSCALE));

    // Build a matrix with the observations in row:
    Mat data = asRowMatrix(db, CV_32FC1);

    // PCA算法保持5主成分分量
    int num_components = 5;

    //执行pca算法
    PCA pca(data, Mat(), CV_PCA_DATA_AS_ROW, num_components);

    //copy  pca算法结果
    Mat mean = pca.mean.clone();
    Mat eigenvalues = pca.eigenvalues.clone();
    Mat eigenvectors = pca.eigenvectors.clone();

    //均值脸
    imshow("avg", norm_0_255(mean.reshape(1, db[0].rows)));

    //五个特征脸
    imshow("pc1", norm_0_255(pca.eigenvectors.row(0)).reshape(1, db[0].rows));
    imshow("pc2", norm_0_255(pca.eigenvectors.row(1)).reshape(1, db[0].rows));
    imshow("pc3", norm_0_255(pca.eigenvectors.row(2)).reshape(1, db[0].rows));
    imshow("pc4", norm_0_255(pca.eigenvectors.row(3)).reshape(1, db[0].rows));
    imshow("pc5", norm_0_255(pca.eigenvectors.row(4)).reshape(1, db[0].rows));

    while(1)
        waitKey(0);

    // Success!
    return 0;
    }

我们输入的10副图像为：

     

    

得到的5副特征脸为：

均值脸为：

 

• 二、OpenCV中应用PCA进行人脸识别

1、OpenCV 从2.4开始支持3个新的人脸识别算法（点击，OpenCV2.4官方讲解，可下载图片库及测试程序）。

1. 1. Eigenfaces 极值特征脸 createEigenFaceRecognizer()
   2. Fisherfaces createFisherFaceRecognizer()
   3. Local Binary Patterns Histograms局部二值直方图 createLBPHFaceRecognizer()

2、为了使用这三种算法，我们首先需要准备人脸训练样本，本文采用AT&T Facedatabase(点击下载)提供的人脸训练样本，该样本包括40个人，每人10张照片。照片在不同时间、不同光照、不同表情(睁眼闭眼、笑或者不笑)、不同人脸细节(戴眼镜或者不戴眼镜)下采集。所有的图像都在一个黑暗均匀的背景下，正面竖直人脸(有些有轻微旋转)。图像格式为pgm，图像大小为92*112，我们可以用gimp打开该格式的图像。

     解压AT&T人脸数据库后，我们把目录att_faces拷贝到solution文件目录。在att_faces目录中，有s1,s2,...s40,共40个子目录，每个子目录中有1.pgm...10.pgm，10个文件，每个子目录对应一个人，子目录中的每副照片，对应一个人的各种人脸表情。比如s1中存放的10张人脸样本如下所示：

      下面我们我们创建一个txt文件facerec_at.txt，格式如下，每一行包括两个字段，中间用“;”分开，第一个字段表示样本图片的路径文件名，第二个参数是一个整数索引，表示第几个人，例如第二个参数都为0，则表示第一个人，后面依次类推：

../att_faces/s13/2.pgm;12 
../att_faces/s13/7.pgm;12 
../att_faces/s13/6.pgm;12 
../att_faces/s13/9.pgm;12 
../att_faces/s13/5.pgm;12 
../att_faces/s13/3.pgm;12 
../att_faces/s13/4.pgm;12 
../att_faces/s13/10.pgm;12 
../att_faces/s13/8.pgm;12 
../att_faces/s13/1.pgm;12 
../att_faces/s17/2.pgm;16 
../att_faces/s17/7.pgm;16

...

../att_faces/s38/10.pgm;37 
../att_faces/s38/8.pgm;37 
../att_faces/s38/1.pgm;37

3. Eigenfaces算法描述：

      二维灰度图像p*q大小，是一个m=pq维的向量空间，一个100*100像素大小的图像就是10000维的图像空间。我们可以通过主成分分析算法(PCA)来对m维的图像向量进行降维操作。OpenCV中PCA算法细节，可以参考：http://www.cnblogs.com/mikewolf2002/p/3432243.html，通过PCA算法，我们可以得到k个特征脸，k就是我们选择降到的维数。

算法描述Algorithmic Description

令   表示一个随机特征，其中  .

1. 计算均值向量 

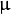
1. 计算协方差矩阵 S

1. 计算 的特征值    和对应的特征向量    

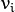
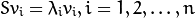
1. 对特征值进行递减排序，特征向量和它顺序一致. k个主成分也就是k个最大的特征值对应的特征向量。

x的K个主成份:

其中  .

PCA基的重构:

其中  .

然后特征脸通过下面的方式进行人脸识别：

1. 把所有的训练数据投影到PCA子空间
2. 把待识别图像投影到PCA子空间
3. 找到训练数据投影后的向量和待识别图像投影后的向量最近的那个。

4. 程序开始后，我们把样本图像和索引标签读到两个vector变量中。

    // 得到txt文件的名字 
    string fn_csv = string("facerec_at_t.txt"); 
    // 定义一个Mat格式的vector用来保存图像，int格式的vector表示图像索引标签 
    vector images; 
    vector labels; 
    //读入图像文件和索引标签 
    try { 
        read_csv(fn_csv, images, labels); 
        } catch (cv::Exception& e) 
        { 
            cerr << "Error opening file \"" << fn_csv << "\". Reason: " << e.msg << endl; 
            exit(1); 
        } 
    我们选择images中的最后一副图片，作为检测的图像，并把它从images中移除。

Mat testSample = images[images.size() - 1]; 
int testLabel = labels[labels.size() - 1]; 
images.pop_back(); 
labels.pop_back();

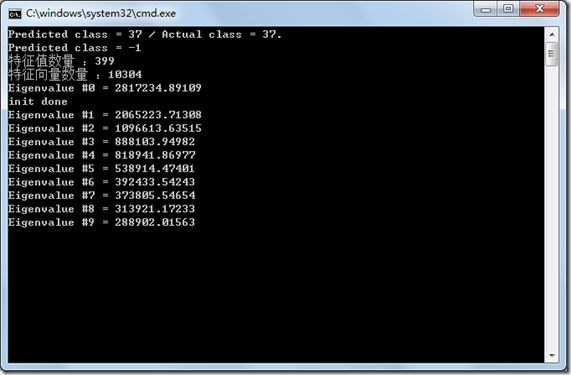
通过下面的代码，我们输入待检测的图像，返回结果是对应人的索引标签，我们输入图像是第37个人，从结果看是对的。

    //创建特征脸算法模型，并通过样本训练数据 
    Ptr model = createEigenFaceRecognizer(); 
    model->train(images, labels);

    //通过predict输入待检测的图像，返回结果是索引标签 
    int predictedLabel = model->predict(testSample); 
    string result_message = format("Predicted class = %d / Actual class = %d.", predictedLabel, testLabel); 
    cout << result_message << endl;

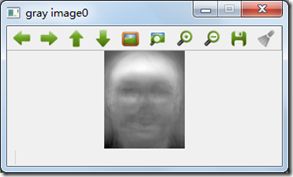
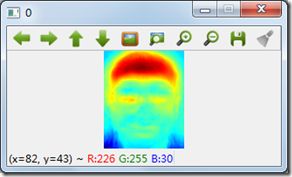
5. 通过下面的代码，我们可以求得特征值和特征向量值，并把特征向量显示为特征脸。

// 特征值和特征向量 
Mat eigenvalues = model->getMat("eigenvalues"); 
// And we can do the same to display the Eigenvectors (read Eigenfaces): 
Mat W = model->getMat("eigenvectors"); 
//特征值列数是1，行数是特征值的数量399 
//特征向量10304*399,每一列都是一个特征向量 
//每一个特征值对应一个特征向量 
printf("特征值数量 ：%d\n", eigenvalues.rows); 
printf("特征向量维数 ：%d\n",W.rows); 
//显示10个特征向量 
for (int i = 0; i < min(10, W.cols); i++) 
    { 
    string msg = format("Eigenvalue #%d = %.5f", i, eigenvalues.at(i)); 
    cout << msg << endl; 
   // 得到第i个特征向量 
    Mat ev = W.col(i).clone(); 
    // 把特征向量归一化到0-255，便于显示 
    Mat grayscale = toGrayscale(ev.reshape(1, height)); 
    // 用Jet colormap显示灰度图. 
    imshow(format("gray image%d", i), grayscale); 
    Mat cgrayscale; 
    applyColorMap(grayscale, cgrayscale, COLORMAP_JET); 
    imshow(format("%d", i), cgrayscale); 
    } 

我们总共显示了10个特征向量(特征脸)，第一个特征脸的灰度图和color map图如下：