【数据分析-学术前沿趋势分析】 Task5 作者信息关联

Datawhale一月份的组队学习~
关键词：数据分析、爬虫、文本分析
开源地址： https://github.com/datawhalechina/team-learning-data-mining/tree/master/AcademicTrends

---

1. 任务说明

• 学习主题：作者关联（数据建模任务），对论文作者关系进行建模，统计最长出现的作者关系
• 学习内容：构建作者关系图，挖掘作者关系
• 学习成果：论文作者知识图谱、图关系挖掘

---

2. 数据处理步骤

将作者列表进行处理，并完成统计，具体步骤如下：

• 将论文第一个作者和其他作何（非第一作者）构建图
• 使用图算法统计图中作者与其他作者的联系

---

3. 社交网络分析

图是复杂网络研究中的一个重要概念。
Graph是用点和线来刻画离散事物集合中的每对事物间以某种方式相联系的数学模型。
Graph在现实世界中随处可见，如交通运输图、旅游图、流程图等。
利用图可以描述现实生活中的许多事物，如用点可以表示交叉口，点之间的连线表示路径，这样就可以轻而易举的描绘出一个交通运输网络。

3.1图类型

• 无向图：忽略了两节点间边的方向性
• 有向图：考虑了边的有向性
• 多重无向图，即两个节点之间的边数多于一条，又允许定点通过同一条边和自己关联

3.1 图统计指标

• 度：是指和该节点相关联的边的条数，又称关联度。对于有向图，节点的入度 是指进入该节点的边的条数；节点的出度是指从该节点出发的边的条数；

• 迪杰斯特拉路径：.从一个源点到其它各点的最短路径，可使用迪杰斯特拉算法来求最短路径；

• 连通图：在一个无向图 G 中，若从顶点i到顶点j有路径相连，则称i和j是连通的。如果 G 是有向图，那么连接i和j的路径中所有的边都必须同向。如果图中任意两点都是连通的，那么图被称作连通图。如果此图是有向图，则称为强连通图。

对于其他图算法，可以在networkx和igraph两个库中找到。

---

4. networkx库

详见这几篇文章，此处只记录下第五节中将用到的一些知识点

• 使用手册
• Python Network（一）基础入门（节点和边基本概念，网络统计量）
• Python Network（二）绘图draw系列draw()，draw_networkx()，draw_networkx_nodes()，draw_networkx_edges()

• 各种图像创建

G=nx.Graph() # 无向图 
G=nx.DiGraph() # 有向图  
G=nx.MultiGraph() # 多图 
G=nx.MultiDiGraph()# 多图有向

• 使用nx.draw绘图
  默认情况下，将图形绘制为没有节点标签或边缘标签且使用完整Matplotlib图形区域且无轴标签的简单表示形式。要想绘制允许标题，轴标签等的更多功能齐全的图形，使用draw_networkx()

语法格式：

draw(G,pos = None,ax = None,hold = None,** kwds ）

参数含义

参数	类型	意义
G	必选	网络图
pos	字典，可选	以节点为键，位置为值的字典。如果未指定，将计算弹簧布局位置。有关计算节点位置的功能，请参见networkx.layout
ax	Matplotlib Axes对象，可选	在指定的Matplotlib轴上绘制图形。
hold	布尔，可选	设置Matplotlib保持状态。如果为True，则随后的绘制命令将添加到当前轴。
**kwds	可选关键字	有关可选关键字的描述，请参见networkx.draw_networkx（）

其中pos可选内容
nx.circular_layout(nf)节点在圆环上均匀分布
nx.kamada_kawai_layout(nf) 这个低版本的network好像没有
nx.random_layout(nf)节点随机分布
nx.spectral_layout(nf)根据图的拉普拉斯特征向量排列节点（我也不知道这个是个啥）
nx.spring_layout(nf)用Fruchterman-Reingold算法排列节点（样子类似多中心放射状）
nx.shell_layout(nf)节点在同心圆上分布

---

5. 代码实现

#导入包
import seaborn as sns #用于画图
from bs4 import BeautifulSoup #用于爬取arxiv的数据
import re #用于正则表达式，匹配字符串的模式
import requests #用于网络连接，发送网络请求，使用域名获取对应信息
import json #读取数据，我们的数据为json格式的
import pandas as pd #数据处理，数据分析
import matplotlib.pyplot as plt #画图工具

#文件读取，这里只读取了'id', 'authors_parsed'两列
def readArxivFile(path, columns=['id', 'submitter', 'authors', 'title', 'comments', 'journal-ref', 'doi',
       'report-no', 'categories', 'license', 'abstract', 'versions',
       'update_date', 'authors_parsed'], count=None):
    '''
    定义读取文件的函数
        path: 文件路径
        columns: 需要选择的列
        count: 读取行数
    '''
    
    data  = []
    with open(path, 'r') as f: 
        for idx, line in enumerate(f): 
            if idx == count:
                break
                
            d = json.loads(line)
            d = {
     col : d[col] for col in columns}
            data.append(d)

    data = pd.DataFrame(data)
    return data

data = readArxivFile('./archive/arxiv-metadata-oai-snapshot.json', 
                     ['id', 'authors_parsed'],
                    200000)
data.head()

可以发现同一篇论文通常对应了多个作者，即第一作者、第二作者…

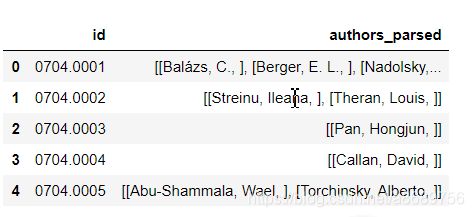
下面先拿五篇论文来进行构建，因为原来的authors_parsed作者的姓名是分开的需要先进行拼接

• iterrows(): 将DataFrame迭代为(insex, Series)对。
• itertuples(): 将DataFrame迭代为元祖。
• iteritems(): 将DataFrame迭代为(列名, Series)对

for row in data.iloc[:5].itertuples(): #itertuples(): 将DataFrame迭代为元祖
    authors=row[2]
    authors=[' '.join(x[:-1])for x in authors]
    print(authors)

看下结果

下面绘制无向图，需要先引入networkx包，此处要绘制无向图，所以使用nx.Graph()

下面使用add_edge将统一篇文章的第一作者和其他作者连接起来，并使用nx.draw来绘制关系图

因此这部分完整代码如下

import networkx as nx 
G = nx.Graph()
for row in data.iloc[:5].itertuples():
    authors = row[2]
    authors = [' '.join(x[:-1]) for x in authors]
    
    #将第一个作者与其他作者连接
    for author in authors[1:]:
        G.add_edge(authors[0],author)
#将作者关系图进行绘制
nx.draw(G,with_labels=True) #with_label作用是添加标签

计算两个点之间的最短路径，也就是迪杰斯特拉路径

try:
    print(nx.dijkstra_path(G, 'Balázs C.', 'Berger E. L.'))
except:
    print('No path')

下面对500片论文构建图，则可以得到更加完整作者关系，并选择最大联通子图进行绘制，折线图为子图节点度值。
先把无向图做好

G = nx.Graph()
for row in data.iloc[:500].itertuples():
    authors = row[2]
    authors = [' '.join(x[:-1]) for x in authors]
    
    #将第一个作者与其他作者连接
    for author in authors[1:]:
        G.add_edge(authors[0],author)

将图中的点按照度数进行排序，得到的degree_sequence长度为1284，,查看下前五个直到最大的度数为27

#按照度数进行排序
#按照度数进行排序
degree_sequence=sorted([d for n ,d in G.degree()],reverse=True)
print(len(degree_sequence))
degree_sequence[:5]

下面绘制双对数坐标图，通过对数坐标可以更清楚的看到较小值的变化

#图像绘制

plt.loglog(degree_sequence, "b-", marker="o")
plt.title("Degree rank plot")
plt.ylabel("degree")
plt.xlabel("rank")

可以看出大部分的度数为10^0也就是1

在上面图的基础上用nx.spring_layout(nf)来实现Fruchterman-Reingold算法排列节点（样子类似多中心放射状），使用networkx.Graph.subgraph来获取最大连通子图

#图像绘制

plt.loglog(degree_sequence, "b-", marker="o")
plt.title("Degree rank plot")
plt.ylabel("degree")
plt.xlabel("rank")

plt.axes([0.45,0.45,0.45,0.45]) #共四个参数四个参数的话，前两个指的是相对于坐标原点的位置，后两个指的是坐标轴的长/宽
Gcc = G.subgraph(sorted(nx.connected_components(G), key=len, reverse=True)[0]) #获取最大连通子图

pos=nx.spring_layout(Gcc) #节点间的间距
plt.axis('off')
nx.draw_networkx_nodes(Gcc,pos,node_size=20)
nx.draw_networkx_edges(Gcc,pos,alpha=0.4)
plt.show()