LDPC译码:和积译码算法(SPA)、最小和算法(MSA)、分层译码算法(LBP)、动态信息更新策略IDS(含RBP、NW-RBP、SVNF-RBP)的MATLAB实现
LDPC译码:和积译码算法(SPA)、最小和算法(MSA)、分层译码算法(LBP)、动态信息更新策略IDS(含RBP、NW-RBP、SVNF-RBP)的MATLAB实现
- 主要内容
- 符号说明
- 算法说明与代码实现
-
- 和积译码算法(SPA)
-
- 基本原理
- MATLAB代码实现SPA
- 分层译码算法(LBP)
-
- 基本原理
- MATLAB代码实现LBP
- IDS类算法
-
- 单次迭代的终止条件及判决方法
- 残差置信传播(RBP)
-
- 算法内容
- RBP的贪婪性
- NW-RBP (Node wise RBP)
- SVNF-RBP (Silent-Variable-Node-Free RBP)
- MATLAB代码实现
- 代码使用说明
- 参考文献
主要内容
LDPC[1]码是一种接近香农极限的“好”码,自二十世纪九十年代被重发现以来,已获得越来越广泛的应用,成为诸多通信领域推荐使用的信道编码。近来,3GPP将其作为5G新空口eMMB应用上的数据传输编码方案。本文将主要介绍LDPC的一些主要译码方法并通过MATLAB实现,这里主要使用的译码方法为SPA([2] Sum-Product Algorithm和积译码算法)、LBP([3] Layered-Belief Propagation分层置信传播译码算法)以及性能更高的IDS(Information Dynamic Schdule)类译码算法如RBP([4] Residual Belief Propagation)、NW-RBP([5] Node Wise-RBP)、SVNF-RBP([6] Silent-Variable-Node-Free RBP)。
符号说明

Check to Variable: C2V
Variable to Check: V2C
算法说明与代码实现
和积译码算法(SPA)
基本原理
LDPC码的概率域BP算法的变量节点和校验节点操作有大量乘法,这样计算量和复杂度都很高,如果将上述0和1的概率信息用对数似然比表示,就可以把乘法运算转换为加法运算,大大降低了运算量,此算法称为和积译码算法。步骤如下:
-
初始化
L v j → c i = C v j L_{v_{j} \rightarrow c_{i}}=C_{v_{j}} Lvj→ci=Cvj (1) -
校验节点更新
m c i → v j = 2 × atanh ( ∏ v b ∈ N ( c i ) \ v j tanh ( L v b → c i 2 ) ) m_{c_{i} \rightarrow v_{j}}=2 \times \operatorname{atanh}\left(\prod_{v_{b} \in N\left(c_{i}\right) \backslash v_{j}} \tanh \left(\frac{L_{v_{b} \rightarrow c_{i}}}{2}\right)\right) mci→vj=2×atanh(∏vb∈N(ci)\vjtanh(2Lvb→ci)) (2) -
变量节点更新
L v j → c i = ∑ c a ∈ N ( v j ) \ c i m c a → v j + C v j L_{v_{j} \rightarrow c_{i}}=\sum_{c_{a} \in N\left(v_{j}\right)\backslash c_{i}} m_{c_{a} \rightarrow v_{j}}+C_{v_{j}} Lvj→ci=∑ca∈N(vj)\cimca→vj+Cvj (3) -
后验概率信息更新
L j = ∑ c a ∈ N ( v j ) m c a → v j + C v j L_{j}=\sum_{c_{a} \in N\left(v_{j}\right)} m_{c_{a} \rightarrow v_{j}}+C_{v_{j}} Lj=∑ca∈N(vj)mca→vj+Cvj (4)
MATLAB代码实现SPA
function Dec_out = LdpcDecode_SPA(in,H,MaxIter)
%%% in为解调后的的对数似然比信息,为N维行向量
%%% H为校验矩阵,MaxIter为最大迭代次数
[M,N] = size(H);
%% 初始化
V_n = in; %似然概率
V_mn = repmat(V_n,M,1); %m代表校验节点索引,n代表变量节点索引
V_mn(H == 0) = 0;
U_mn = zeros(M,N);
%% 译码
for i = 1:MaxIter
% 校验节点更新
for m = 1:M
Nm = find(H(m,:)==1); %校验节点m相邻的变量节点
for n = 1:length(Nm)
aa = Nm;
aa(n) = [];
% MSA: U_mn(m,Nm(n)) = prod(sign(V_mn(m,aa)))*min(abs(V_mn(m,aa)));
U_mn(m,Nm(n)) = 2*atanh(prod(tanh(V_mn(m,aa)/2)));
end
end
%变量节点更新
for n = 1:N
Mn = find(H(:,n)==1); %变量节点n相邻的校验节点
for m = 1:length(Mn)
bb = Mn;
bb(m) = [];
V_mn(Mn(m),n) = in(n) + sum(U_mn(bb,n));
end
V_n(n) = in(n) + sum(U_mn(Mn,n));%似然概率更新
end
end
%% 硬判决
decBits = zeros(1,N);
decBits(V_n <= 0) = 1; %信息位+校验位的译码输出
Dec_out = decBits(1:N-M); %仅含信息位的译码输出
注意最小和算法(MSA)与SPA的区别仅在于校验节点更新,MSA算法利用tanh、atanh的单调性,将其非线性运算转化为最招序列中最小值而减少计算量,将MSA的校验节点更新公式为:
m c i , v j = min v s ∈ N ( c i ) v j ( L v b → c i ∣ ) × ∏ v b ∈ N ( c i ) v j sgn ( L v b − c i ) m_{c_{i}, v_{j}}=\min _{v_{s} \in N\left(c_{i}\right) v_{j}}\left(L_{v_{b} \rightarrow c_{i}} |\right) \times \prod_{v_{b} \in N\left(c_{i}\right) v_{j}} \operatorname{sgn}\left(L_{v_{b}-c_{i}}\right) mci,vj=minvs∈N(ci)vj(Lvb→ci∣)×∏vb∈N(ci)vjsgn(Lvb−ci) (5)
已在代码中作出注释,需要时进行替换即可。
分层译码算法(LBP)
基本原理
在SPA中本次的更新值仅可以在下次迭代中使用,LBP采用分层译码的方法,即将H按照水平方向分为数个子层,每层可单独进行SPA译码,上层译码更新后的信息在下层译码时即可使用,其收敛速度是SPA算法的两倍。这里我们将每个校验节点设为一个单独的层。在每一层中:
变量节点更新: L v j → c i = c v j − m c i → v j L_{v_{j} \rightarrow c_{i}}=c_{v_{j}}-m_{c_{i} \rightarrow v_{j}} Lvj→ci=cvj−mci→vj
校验节点更新: m c i → v j = ∏ v b ∈ N ( c i ) \ v j sign ( L v b → c i ) × [ ∑ v b ∈ N ( c i ) \ v j − ln tanh ( ∣ L v b → c i ∣ 2 ) ] m_{c_{i} \rightarrow v_{j}}=\prod_{v_{b} \in {N}\left(c_{i}\right) \backslash v_{j}} \operatorname{sign}\left(L_{v_{b} \rightarrow c_{i}}\right) \times\left[\sum_{v_{b} \in N\left(c_{i}\right) \backslash v_{j}}-\ln \tanh \left(\frac{\left|L_{v_{b} \rightarrow c_{i}}\right|}{2}\right)\right] mci→vj=∏vb∈N(ci)\vjsign(Lvb→ci)×[∑vb∈N(ci)\vj−lntanh(2∣Lvb→ci∣)]
后验概率更新则变为: L j = L v j → c i + m c i → v j L_{j}=L_{v_{j} \rightarrow c_{i}}+m_{c_{i} \rightarrow v_{j}} Lj=Lvj→ci+mci→vj
硬判决方法不变
MATLAB代码实现LBP
https://github.com/vodafone-chair/5g-nr-ldpc/blob/master/ldpcDecode.m 注意这里的代码经过了少许修改
function Dec_out = LdpcDecode_LBP(in,H,MaxIter)
[M,N] = size(H);
minVal = realmin('double');
numEntries = nnz(H);
Rcv = spalloc(M, N, numEntries);
Qv = in;
% Decode
for ldpcCurIter = 1:MaxIter
% Loop over all check nodes
for checkIdx = 1:M
% Find all neighbouring variable nodes of current check node
nbVarNodes = find(H(checkIdx,:)==1);
% Tmp update llr
tmpLlr = Qv(nbVarNodes) - full(Rcv(checkIdx,nbVarNodes));
% Compute S = (Smag, Ssign)
Smag = sum(-log(minVal+tanh(abs(tmpLlr)/2)));
% Count number of negative elements
if mod(sum(tmpLlr<0),2) == 0
Ssign = +1;
else
Ssign = -1;
end
% Loop all neighbouring variable nodes
for varIter = 1:length(nbVarNodes)
varIdx = nbVarNodes(varIter);
Qtmp = Qv(varIdx) - Rcv(checkIdx, varIdx);
QtmpMag = -log(minVal+tanh(abs(Qtmp)/2));
% Note: +minVal in order to deal with llr=0;
% implementation can be improved
QtmpSign = sign(Qtmp+minVal);
% Update message passing matrix
% From reference: Rcv = phi^-1(S-phi(Qtmp))
Rcv(checkIdx, varIdx) = Ssign*QtmpSign * (-log(minVal+tanh(abs(Smag-QtmpMag)/2)));
% Update Qv. From reference: Qv = Qtmp + Rcv
Qv(varIdx) = Qtmp + Rcv(checkIdx, varIdx);
end
end
Dec_out = zeros(1,N-M);
Dec_out(Qv(1:N-M)<0) = 1;
end
代码中的译码顺序是从H矩阵的第一行顺序译码,事实上可以根据码的结构调整译码顺序,合理的安排译码顺序会提高误码性能。
IDS类算法
在SPA或者LBP的迭代过程中,一些节点产生的信息可能在少量迭代时即已趋于稳定,而另一部分信息可能徐国更多次的迭代才能稳定下来,而SPA或LBP并不对节点进行区分。IDS类方法考虑节点(变量节点或校验节点)信息的变化,有选择的挑选Tanner图中的边进行信息的更新,实验证明,这类方法在收敛速度与误码性能上较前两种方法更高。
后面介绍的几种IDS类方法均是基于贪婪的准则选择相应的边进行更新,考虑的均为校验节点处的信息变化。
单次迭代的终止条件及判决方法
假设Tanner图中边的总数为E,即校验矩阵H中非零元素数量。通过分析可以发现SPA、LBP的C2V更新次数均为E,下面介绍的IDS类方法考虑的均为校验节点信息的变化,因此当校验节点的更新次数(注意不包括计算残差时的校验节点更新)达到E时本次迭代结束。
其后验概率更新、硬判决方式与SPA相同,不再赘述。
残差置信传播(RBP)
算法内容
RBP是每次选择校验节点中信息变化最大的边进行更新,考察信息量变化的准则是相邻两次校验节点更新的值得变化量,称为残差,即:
r c i → v j = ∣ m c i → v j p r e − m c i → v j ∣ r_{c_{i} \rightarrow v_{j}}=\left|m_{c_{i} \rightarrow v_{j}}^{p r e}-m_{c_{i} \rightarrow v_{j}}\right| rci→vj=∣∣∣mci→vjpre−mci→vj∣∣∣ (6)
可以看到计算残差即是做校验节点更新,然后取与上一次校验节点更新的变化量。但获得残差仅仅是为了进行比较得到具有最大残差的边,而并不进行传播,如上所述,采用SPA更新校验节点的计算量比较大,因此我们使用(5)式即MSA采用的校验节点更新方法计算残差,进行传播时再采用(2)式计算精确的校验节点更新值。实验证明,这种方式对实验结果影响很小,却大幅度较少了计算量。下面介绍的另外几种IDS方法也采取同样的残差计算策略。
在每次迭代中首先选取具有最有最大残差值的边,假设该边是 c i → v j c_{i} \rightarrow v_{j} ci→vj,使用(2)式计算 m c i → v j m_{c_{i} \rightarrow v_{j}} mci→vj并置 r c i → v j = 0 r_{c_{i} \rightarrow v_{j}}=0 rci→vj=0;之后使用(3)式计算变量节点更新 v j → c a v_{j} \rightarrow c_{a} vj→ca其中 c a ∈ N ( v j ) \ c i c_{a} \in N\left(v_{j}\right) \backslash c_{i} ca∈N(vj)\ci;最后使用式(6)更新残差值 r c a → v b r_{c_{a}} \rightarrow v_{b} rca→vb,其中 v b ∈ N ( c a ) \ v j v_{b} \in N\left(c_{a}\right) \backslash v_{j} vb∈N(ca)\vj。判断终止条件是否达到,否则继续执行上述过程。该过程可整理如下:

下面举例说明更新过程(本文中用红色线条表示执行校验节点更新的边,蓝色线条表示变量节点更新的边,黄色线条表示残差更新的边),一码字的Tanner图如下图所示:
- 假设经计算选择了边 C 4 → V 3 \mathcal{C}_{4} \rightarrow \mathcal{V}_{3} C4→V3:
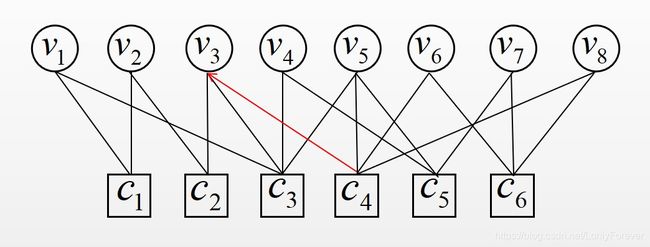 更新 m c 4 → v 3 m_{c_{4} \rightarrow v_{3}} mc4→v3并置 r c 4 → v 3 = 0 r_{c_{4} \rightarrow v_{3}}=0 rc4→v3=0
更新 m c 4 → v 3 m_{c_{4} \rightarrow v_{3}} mc4→v3并置 r c 4 → v 3 = 0 r_{c_{4} \rightarrow v_{3}}=0 rc4→v3=0 - 根据(3)式更新 v 3 → c 2 \mathcal{v}_{3} \rightarrow \mathcal{c}_{2} v3→c2与 v 3 → c 3 \mathcal{v}_{3} \rightarrow \mathcal{c}_{3} v3→c3
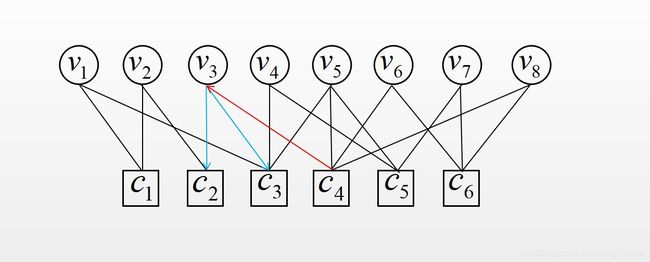
- 根据(5)(6)式更新 r c 2 → v 2 r_{c_{2} \rightarrow v_{2}} rc2→v2, r c 3 → v 4 r_{c_{3} \rightarrow v_{4}} rc3→v4, r c 3 → v 5 r_{c_{3} \rightarrow v_{5}} rc3→v5。
RBP的贪婪性
RBP的策略即是优先更新低可靠性的信息用以“纠正”变量节点,这在直观上是可行的,但由于其选择边的贪婪特性,当图中存在“贪婪组”时,最大残差边的选取很可能在一个该贪婪组中重复选择,这样虽然校验节点或变量节点的信息在不断更新,但却没有新的信息加入,这样当迭代次数增大时并不能提升译码性能。仍采用上面的例子来进一步解释贪婪组:
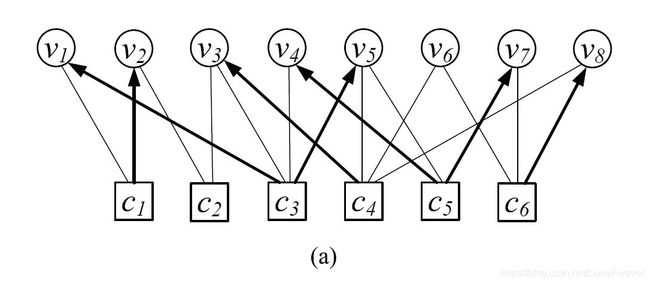
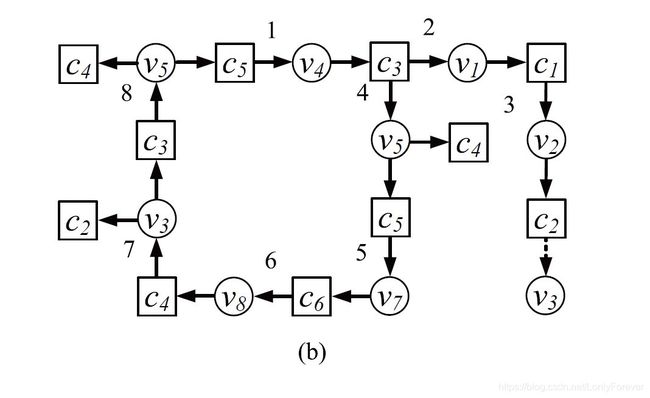 该图a中用粗实线表示表示贪婪组中的边共7条,贪婪组中边的总数仅占总边数的一小部分。最大残差边的选取在该贪婪组中以一种固定的顺序被选取,该顺序如图b所示。在该贪婪组中,最大残差值虽然在不断变化,但该贪婪组中却并没有新的信息加入,信息的不完整性注定其不能达到最优的性能,而RBP却在其中浪费了大量的计算资源。实验结果表明,由于对产生信息的节点进行的选择,RBP有着更快的收敛速度,但由于贪婪性,其十分容易陷入贪婪组中,因而相比于SPA、LBP有着更高的误码平层(error floor)。由于SPA、LBP对节点不进行选取,不具贪婪性,因此这些方法不会产生贪婪组。
该图a中用粗实线表示表示贪婪组中的边共7条,贪婪组中边的总数仅占总边数的一小部分。最大残差边的选取在该贪婪组中以一种固定的顺序被选取,该顺序如图b所示。在该贪婪组中,最大残差值虽然在不断变化,但该贪婪组中却并没有新的信息加入,信息的不完整性注定其不能达到最优的性能,而RBP却在其中浪费了大量的计算资源。实验结果表明,由于对产生信息的节点进行的选择,RBP有着更快的收敛速度,但由于贪婪性,其十分容易陷入贪婪组中,因而相比于SPA、LBP有着更高的误码平层(error floor)。由于SPA、LBP对节点不进行选取,不具贪婪性,因此这些方法不会产生贪婪组。
下面介绍的NW-RBP与SVNF-RBP是针对于RBP算法的改进版,尽量避免信息的更新陷入贪婪组。
NW-RBP (Node wise RBP)
为避免陷入贪婪组中,可以选择多条边进行信息更新。在每次迭代中首先选取具有最有最大残差值的边,假设该边是 c i → v j c_{i} \rightarrow v_{j} ci→vj,使用(2)式计算 m c i → v k m_{c_{i} \rightarrow v_{k}} mci→vk,其中 v k ∈ N ( c i ) v_{k} \in N\left(c_{i}\right) vk∈N(ci) 并置 r c i → v k = 0 r_{c_{i} \rightarrow v_{k}}=0 rci→vk=0(注意这里与RBP的区别,RBP是选择 c i → v j c_{i} \rightarrow v_{j} ci→vj一条边,而NW-RBP是选择校验节点 c i c_{i} ci连接的所有边);之后做变量节点更新 L v k → c a L_{v_{k} \rightarrow c_{a}} Lvk→ca,其中 c a ∈ N ( v k ) \ c i c_{a} \in N\left(v_{k}\right) \backslash c_{i} ca∈N(vk)\ci;最后更新 r c a → v b r_{c_{a} \rightarrow v_{b}} rca→vb,其中 v b ∈ N ( c a ) \ v k v_{b} \in N\left(c_{a}\right) \backslash v_{k} vb∈N(ca)\vk。判断终止条件是否达到,否则继续执行上述过程。该过程可整理如下:

下面举例说明边的选取过程:
- 假设经计算选择了边 C 4 → V 3 \mathcal{C}_{4} \rightarrow \mathcal{V}_{3} C4→V3,则用(2)式计算 m c i → v k m_{c_{i} \rightarrow v_{k}} mci→vk,其中 v k ∈ N ( c i ) v_{k} \in N\left(c_{i}\right) vk∈N(ci) :
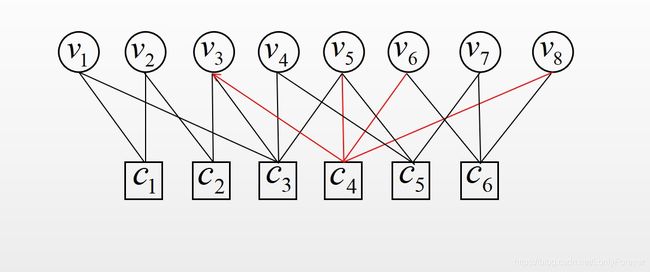
- 使用(3)式计算 L v k → c a L_{v_{k} \rightarrow c_{a}} Lvk→ca,其中 c a ∈ N ( v k ) \ c i c_{a} \in N\left(v_{k}\right) \backslash c_{i} ca∈N(vk)\ci:
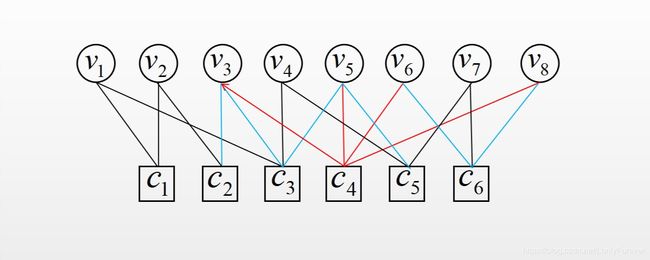
- 使用(5)(6)计算 r c a → v b r_{c_{a} \rightarrow v_{b}} rca→vb,其中 v b ∈ N ( c a ) \ v k v_{b} \in N\left(c_{a}\right) \backslash v_{k} vb∈N(ca)\vk:
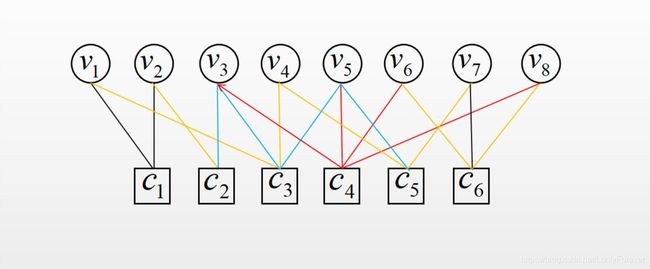 这样通过选取更多的边就可以降低进入贪婪组的概率。
这样通过选取更多的边就可以降低进入贪婪组的概率。
SVNF-RBP (Silent-Variable-Node-Free RBP)
RBP通过更新更多的边来来避免陷入贪婪组,但这些边携带的信息可能对译码提升的性能贡献可能很小。另外在迭代过程中我们发现,一些变量节点可能永远没有机会得到更新,这样的变量节点称为Silent Variable Nodes,这些节点的存在会影响译码性能。不同于NW-RBP选取最大残差边对应的校验节点连接的所有边进行校验节点更新,SVNF-RBP让每一个变量节点都有同样的机会去选取其连接的具有最大残差的边,这样就保证了所有被选取的边所携带的信息尽可能的大,同时消除了Silent Variable Nodes。且由于其选取的校验节点更新的边更多,故会进一步降低陷入贪婪组中的危险。
其执行过程如图所示:
 这里不再画图示范,选取具有最大残差边后的更新过程与RBP算法完全相同。与RBP的区别仅在于,RBP选取的最大残差边拥有全局最大的残值,而SVNF-RBP选取的边仅是该边对应的变量节点所连接的边中,其残差最大。
这里不再画图示范,选取具有最大残差边后的更新过程与RBP算法完全相同。与RBP的区别仅在于,RBP选取的最大残差边拥有全局最大的残值,而SVNF-RBP选取的边仅是该边对应的变量节点所连接的边中,其残差最大。
注意到4~13行执行次数达到 d c ‾ \overline{d_{c}} dc(该LDPC码的平均重量)次时,校验节点更新次数为E次,此时一次迭代完成。
MATLAB代码实现
function Dec_out = LdpcDecode_IDS(in,H,MaxIter,Method)
% The input "in" is a 1*N vector which contains the log-likehood ratio that
% calculated by demodulator. H is the parity check matrix of the LDPC
% codes. MaxIter defines the maximun iteration of the decoder. The decode
% algorith controlled by parameter "Method", the choices are 'RBP','NW-RBP',
% 'SVNF-RBP'
% Reference: "Informed Dynamic Scheduling for Belief-Propagation Decoding
% of LDPC Codes" By Andres. 'RBP','NW_RBP'
% "Two Informed Dynamic Scheduling Strategies for Iterative LDPC Decoders"
% By Huang-Chang Lee. 'SVNF_RBP'
% Author: Wang Bingbing
% Last Update: 2019/10/17
%% Initialization
[M,N] = size(H);
V_mn = repmat(in,M,1);
V_mn(H == 0) = 0;
U_mn = zeros(M,N);
ResC2V = zeros(M,N);
% Initialize the residual martix.
for m = 1:M
Nm = find(H(m,:)==1); % We use "Nm" to represent a check node's neighbour variable nodes.
for n = 1:length(Nm)
aa = Nm;
aa(n) =[];
ResC2V(m,Nm(n)) = prod(sign(V_mn(m,aa)))*min(abs(V_mn(m,aa)));
end
end
%% Decode
% Note that one iteration will be finished after the number of C2V
% message updates equal to the number of edges in LDPC graph
switch Method
case 'RBP'
cntCVmax = nnz(H);
for j = 1:MaxIter
cntCV = 0;
while cntCV ~= cntCVmax
% Choose Ci to Vj
[~,IndMax] = max(abs(ResC2V(:)));
[ci,vj] = ind2sub(size(ResC2V),IndMax);
% Generate and propagate Ci to Vj and then
% set r(ci,vj)=0
Nm_ci = find(H(ci,:)==1);
Nm_ci(Nm_ci == vj) = [];
U_mn(ci,vj) = 2*atanh(prod(tanh(V_mn(ci,Nm_ci)/2)));
ResC2V(ci,vj) = 0;
cntCV = cntCV+1;
% Update information Vj to its neighbour check
% nodes except Ci
Mn_vj = find(H(:,vj)==1);
for c = 1:length(Mn_vj)
ca = Mn_vj(c);
if ca == ci
continue
end
bb = Mn_vj;
bb(c) = [];
V_mn(ca,vj) = in(vj) + sum(U_mn(bb,vj));
% Update residual from ca to its neighbour
% variable nodes ecxept vj
Nm_ca = find(H(ca,:)==1);
for v = 1:length(Nm_ca)
vb = Nm_ca(v);
if vb == vj
continue
end
cc = Nm_ca;
cc(v) =[];
ResC2V(ca,vb) = prod(sign(V_mn(ca,cc)))*min(abs(V_mn(ca,cc)))-ResC2V(ca,vb);
end
end
end
end
case 'SVNF-RBP'
averDv = sum(sum(H))/N; % Average of variable nodes' degree
for j = 1:MaxIter
for loopInd = 1:averDv
for vj = 1:N
% find (Cmax,Vmax)
Mn = find(H(:,vj) == 1);
ResC2V_tmp = ResC2V(Mn,:);
ResC2V_tmp(:,vj) = 0;
[~,IndMax] = max(abs(ResC2V_tmp(:)));
[mt, Vmax] = ind2sub(size(ResC2V_tmp),IndMax);
Cmax = Mn(mt);
% Generate information Cmax to Vmax and propagate,
% then set r(Cmax,Vmax)=0
Nm_Cmax = find(H(Cmax,:) == 1);
Nm_Cmax(Nm_Cmax == Vmax) = [];
U_mn(Cmax,Vmax) = 2*atanh(prod(tanh(V_mn(Cmax,Nm_Cmax)/2)));
ResC2V(Cmax,Vmax) = 0;
% Update information Vmax to its neighbour check
% nodes except Cmax
Mn_Vmax = find(H(:,Vmax) == 1);
for c1 = 1:length(Mn_Vmax)
Ca = Mn_Vmax(c1);
if Ca == Cmax
continue
end
bb = Mn_Vmax;
bb(c1) = [];
V_mn(Ca,Vmax) = in(Vmax) + sum(U_mn(bb,Vmax));
% Update residual from Ca to its neighbour
% variable nodes ecxept Vmax
Nm_Ca = find(H(Ca,:) == 1);
for v1 = 1:length(Nm_Ca)
Vb = Nm_Ca(v1);
if Vb == Vmax
continue
end
cc = Nm_Ca;
cc(v1) =[];
% For reducing complexity, using MS to
% calculate redidual and using SPA to
% propagate.
ResC2V(Ca,Vb) = prod(sign(V_mn(Ca,cc)))*min(abs(V_mn(Ca,cc)))-ResC2V(Ca,Vb);
end
end
end
end
end
case 'NW-RBP'
for j = 1:MaxIter
for i = 1:M
% Choose Ci to Vj
[~,IndMax] = max(abs(ResC2V(:)));
[ci,~] = ind2sub(size(ResC2V),IndMax);
% Generate and propagate ci to its neighbour check nodes
Nm_ci = find(H(ci,:) == 1);
for v1 = 1:length(Nm_ci)
vk = Nm_ci(v1);
aa = Nm_ci(Nm_ci ~= vk);
U_mn(ci,vk) = 2*atanh(prod(tanh(V_mn(ci,aa)/2)));
ResC2V(ci,vk) = 0;
% Generate and propagate vk to its neighbour check
% nodes except ci
Mn_vk = find(H(:,vk) == 1);
for c1 = 1:length(Mn_vk)
ca = Mn_vk(c1);
if ca == ci
continue
end
bb = Mn_vk(Mn_vk ~= ca);
V_mn(ca,vk) = in(vk) + sum(U_mn(bb,vk));
% Compute residual ca to its neighbour variable
% nodes except vk
Nm_ca = find(H(ca,:) == 1);
for v2 = 1:length(Nm_ca)
vb = Nm_ca(v2);
if vb == vk
continue
end
cc = Nm_ca(Nm_ca ~= vb);
ResC2V(ca,vb) = prod(sign(V_mn(ca,cc)))*min(abs(V_mn(ca,cc)))-ResC2V(ca,vb);
end
end
end
end
end
end
V_n = in + sum(U_mn);
decBits = zeros(1,N);
decBits(V_n <= 0) = 1; % Comnination of information bits and check bits
Dec_out = decBits(1:N-M); % Only information bits
end
代码使用说明
本文代码的输入参数主要为三个,即in(解调器解调后得到的对数似然信息比),H(LDPC的校验矩阵)与MaxIter(译码器的最大迭代次数),使用时直接调用即可。必须注意的是参量H是完整的校验矩阵H,而非稀疏矩阵,直接采用稀疏性的参数可以大大降低内存使用量,很容易将代码转换为稀疏性的索引,读者可以自行尝试。
以上程序经验证可以正常运行,虽经过仔细检查核对,但仍不免有所疏漏,请读者在使用时务必留心验证,如发现疏漏之处请立即留言,共同探讨学习。
此外,十分重要的一点是以上代码仅供理解算法学习使用,运行效率其实很低(我在跑仿真时用的其实是C语言,但其要针对不同码字进行特定的调参,并不适合初学者,需要学习的可以去Github上搜索下载,资源很多),大家在掌握算法思想后可以自行探索如何让优化。
参考文献
[1] R. G. Gallager, Low-Density Parity-Check Codes. Cambridge, MA: M.I.T. Press, 1963.
[2] D. J. C. MacKay, “Good error-correcting codes based on very sparse matrices,” IEEE Trans. Inform. Theory, vol. 45, pp. 399–431, Mar. 1999.
[3] D. E. Hocevar. “A reduced complexity decoder architecture via layered decoding of LDPC code” in Proc. IEEE Workshop Signal processing and Systems (SIPS. 04), Austin, TX, Oct. 2004, pp. 107-112.
[4] Casado A I V, Griot M, Wesel R D. Informed Dynamic Scheduling for Belief-Propagation Decoding of LDPC Codes[J]. 2007.
[5] Lee H C , Ueng Y L , Yeh S M , et al. Two Informed Dynamic Scheduling Strategies for Iterative LDPC Decoders[J]. IEEE Transactions on Communications, 2013, 61(3):886-896.
