【2】k近邻回归

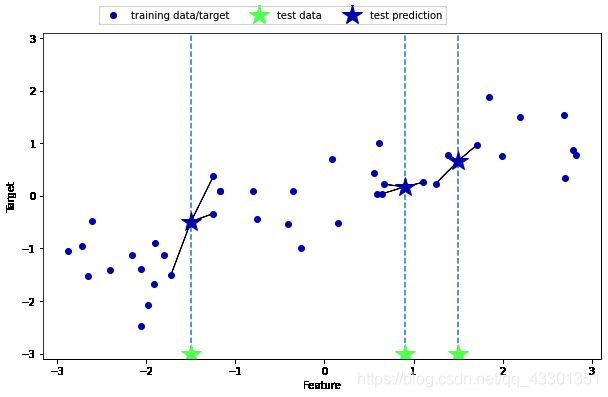
k近邻用于回归，先从单一近邻进行分析，使用wave数据集。有3个测试数据点，在x轴上用绿色五角星表示。预测结果用蓝色五角星表示。

import numpy as np
import pandas as pd
import mglearn
import matplotlib.pyplot as plt

mglearn.plots.plot_knn_regression(n_neighbors=1)

输出

当然也可以用多个近邻进行回归，预测结果为这些邻居的平均值

mglearn.plots.plot_knn_regression(n_neighbors=3)

输出

使用scikit-learn中的KNeighborsRegressor来实施k近邻回归，

from sklearn.neighbors import KNeighborsRegressor
from sklearn.model_selection import train_test_split

X,y = mglearn.datasets.make_wave(n_samples=40)
#将数据集划分为训练集和测试集
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=0)
#模型实例化
reg = KNeighborsRegressor(n_neighbors=3)
#训练模型
reg.fit(X_train,y_train)
#对测试集作出预测
print('测试集预测结果为：{}'.format(reg.predict(X_test)))

输出

测试集预测结果为：[-0.05396539  0.35686046  1.13671923 -1.89415682 -1.13881398 -1.63113382
  0.35686046  0.91241374 -0.44680446 -1.13881398]

使用score方法来评价模型，此时返回的是R²分数，位于0~1之间。R²等于1对应完美预测，R²等于0对应常数模型，即总是预测训练集目标值（y_train）的平均值。

print('测试集 R^2 值：{:.2f}'.format(reg.score(X_test,y_test)))

输出

测试集 R^2 值：0.83

下面考察多个邻居的情况，

fig,axes = plt.subplots(1,3,figsize=(15,4))
#在-3和3之间创建1000个均匀分布的点
line = np.linspace(-3,3,1000).reshape(-1,1) #reshape(-1,1)表示变为1列，-1表示“未指定”
for n_neighbors,ax in zip([1,3,9],axes):
    #使用1、3、9个邻居分别进行训练和预测
    reg = KNeighborsRegressor(n_neighbors=n_neighbors)
    reg.fit(X_train,y_train)
    ax.plot(line,reg.predict(line))
    ax.plot(X_train,y_train,'g>',markersize=8)
    ax.plot(X_test,y_test,'r<',markersize=8)
    ax.set_title(
        '{}neighbor(s)\n train score:{:.2f}, test score:{:.2f}'.format(
        n_neighbors,reg.score(X_train,y_train),
        reg.score(X_test,y_test)))
    ax.set_xlabel('Feature')
    ax.set_ylabel('Target')
axes[0].legend(['Model prediction','Training data/target',
               'Test data/target'],loc='best')

输出

由图中可以看出，和k近邻分类的分类边界类似，邻居越多，训练出的曲线越平滑。

k-NN优点：
模型简单，容易理解。
k-NN缺点：
需要对数据进行预处理；训练集很大的情况下，训练速度很慢；对稀疏数据集的效果尤其不好。