李宏毅2020机器学习02 - Regression
我们在这节课将通过案例研究来理解Regression
为读者更好地掌握本文框架且方便查询,下面提供本文目录:
-
-
- 课程回顾
- 案例研究:预测宝可梦进化后的CP值(用于衡量战斗能力)
-
- 确定senario(学习情境)、task(任务)、model(模型)
- senario
- task
- model
- 明确具体步骤
-
- Step1:选择Model
- Step2:Goodness of Function(评估Function的好坏)
- Step3:Pick the Best Function(Use Gradient Descent)
-
- Gradient Descent(梯度下降)
- 其他问题及解决
-
- The result is so bad!
- Back to Step1:Redesign the Model
- Back to Step2:Regularization
- 总结
-
课程回顾
由上节课我们了解到,Regression适合用于输出为一个scalar的情况。
比如说input是使用者A和商品B,output是使用者A购买商品B的可能性。

案例研究:预测宝可梦进化后的CP值(用于衡量战斗能力)
我们期望根据已有的宝可梦进化前后的数据,来预测某只宝可梦进化后的CP值的大小。
参数解释:
x:宝可梦所列属性的集合
xs:宝可梦种类,例如下面的妙蛙种子
xcp:宝可梦的战斗能力
xw:宝可梦的体重
xh:宝可梦的身高
f:function
y:这里特指进化后的CP值
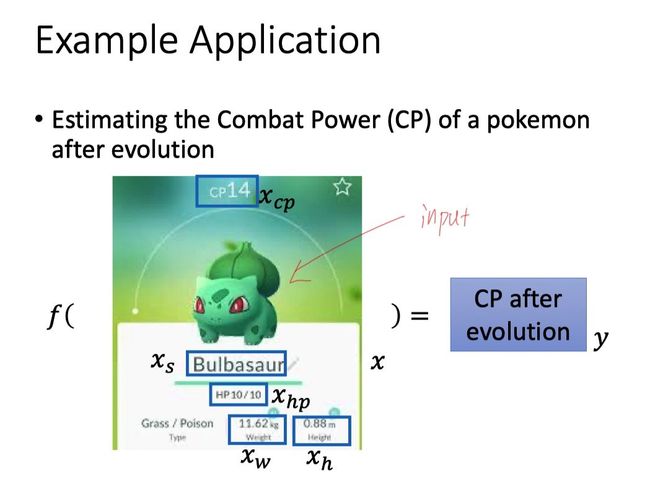
确定senario(学习情境)、task(任务)、model(模型)
senario
首先根据已有的data来确定senario,由于我们拥有这样一批数据:input的是进化前的宝可梦(包含它的各种属性数据),而output的是进化后宝可梦的CP值。因此,我们拥有的data是labeled,选择senario为Supervised Learning。
task
然后根据我们的output来确定task,我们想要得到的是宝可梦进化后的CP值,是一个scalar,因此选用的task是Regression。
model
最后,我们先选择Linear和Non-linear的Regression作分析研究。
明确具体步骤
Step1:Model:定义一个model,即function set
Step2:Goodness of Function:定义一个Loss Function去评估function的好坏
Step3:Pick the ‘‘Best’’ Function:找到一个最好的function
Step1:选择Model
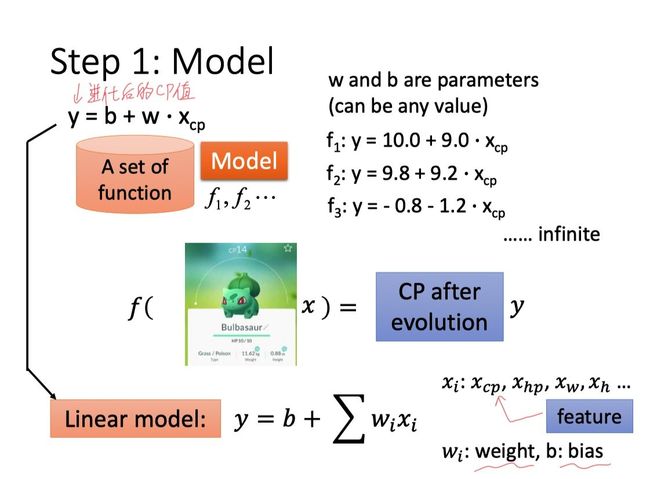
在这里我们选用一个Linear Model:y = b + w.xcp
y代表的是一个function set(函数集合),包含了各种同一结构的function。
比如
- 令b=10.0,w=9.0,那么有f1:y = 10.0 + 9.0 xcp
- 令b=9.8,w=9.2,那么有f2:y=9.8 + 9.2 xcp
- …
参数b和w可以是任何值,通过改变他们的值我们可以得到无数个function,而我们要做的就是选出其中最好的一个。
进一步,我们可以将上面的式子拓展为: y = b + ∑ w i . x i y = b+ \sum{w_i.x_i} y=b+∑wi.xi
参数解释:
xi:包括xcp、xhp、xw、xh…(即feature)
wi:weight
b:bias
Step2:Goodness of Function(评估Function的好坏)
参数说明
x i x^i xi:用上标表示第i只宝可梦(下标表示该object中的component,比如cp值)。
y ^ i \hat{y}^i y^i:表示一个实际的object输出,上标i表示是第i只宝可梦。
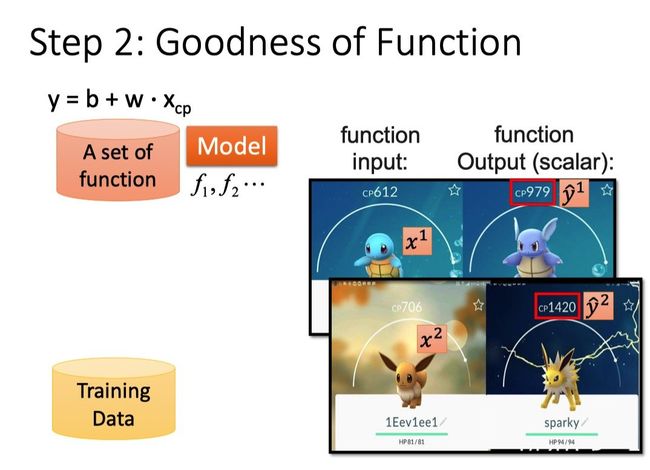
下图展示了预测值与实际值的偏差。

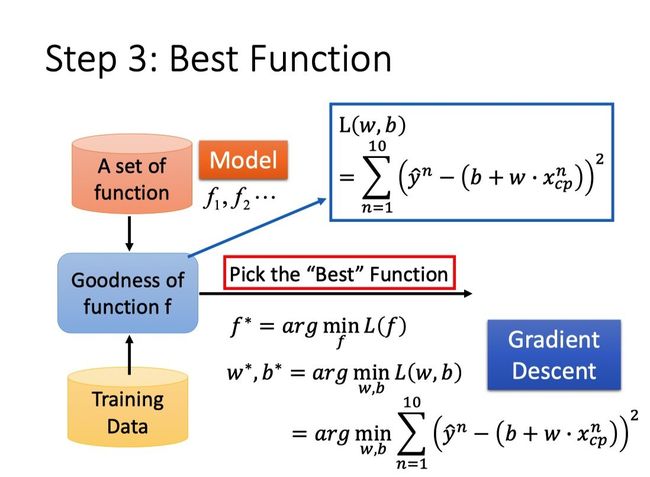
对于Model:y = b + w xcp
Training Data每输入一个xcpn都会输出一个预测值yn,而yn与实际值 y ^ i \hat{y}^i y^i,即理想值或labeled值)又会有偏差,因此我们定义一个Loss Function用于评价function的好坏。
我们可以将Loss Function写成:
L ( f ) = L ( w , b ) = ∑ n = 1 10 ( y ^ n − ( b + w ⋅ x c p n ) ) 2 L(f)=L(w, b)=\sum_{n=1}^{10} \left(\hat{y}^{n}-\left(b+w \cdot x_{cp}^{n}\right)\right)^{2} L(f)=L(w,b)=n=1∑10(y^n−(b+w⋅xcpn))2
我们可以把L看作是f或者w和b的function,L实际上衡量的就是f或者参数w和b的好坏。
L越大,说明该function的表现越差,参数w,b越不好;L越小,说明该function的表现越好,参数w,b越好。

注:就像model(function set)是我们自己选的,Loss Function的定义方式也可以由我们选择。常用的方法是选用类似于方差的形式,就像这里选用实际值减预测值的平方,将10个估测误差相加起来就是Loss Function。
Step3:Pick the Best Function(Use Gradient Descent)
经过前面的步骤我们已经找到了Loss Function用于衡量model的好坏,接下来我们要做的就是找到最好的函数f*或者w和b,使得这个Loss Function最小。
可以采用的方法是Gradient Descent(梯度下降)。
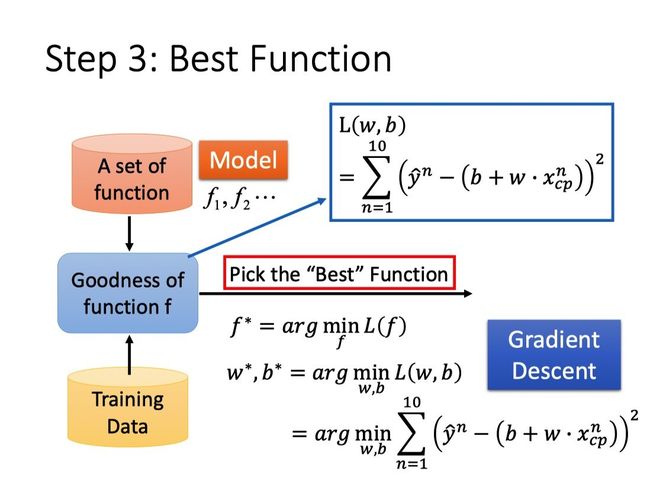
Gradient Descent(梯度下降)
当我们只考虑单个参数w时,我们的做法如下:
-
先随机取一个初始值参数值w0
-
再计算L在该点的微分,然后往loss下降的方向走,举个例子:
- 如果微分值为负,那么‘’小猴子‘’选择往w增加的方向走,也就是向右下方走。
-
如果微分值为正,那么‘‘小猴子’'选择往w减小的方向走,也就是向左下方走。
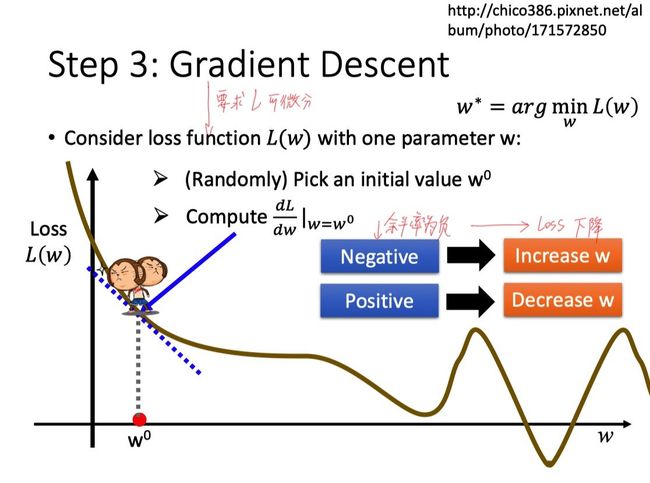
那么我们每一步走多大呢?这里引入一个参数η(即学习速率lr),用于衡量每一步的大小。

走完一步后,参数w0更新为w1,接下来要做的就是不断重复上面的步骤,直到取得我们满意的loss。
对于多参数问题,方法类似

Gradient Descent中可能遇到的问题
是不是我们update参数的次数越多,我们取得的loss就越小呢?
答案是否定的。由于我们想要找到的是使得loss最小的最小值点,但是,假设loss的曲线存在多个使得L关于参数的偏微分等于0的点,比如,驻点、极大值点或者偏微分约等于0的点,我们就有可能找错点。
另外,如果学习速率η太大了,我们一更新参数,可能直接就跨过了最小值点。

其他问题及解决
The result is so bad!
问:为什么model越复杂,在testing data上结果越好,但是testing data上表现越糟糕?
注意:从function2开始,已经不再是linear的了。
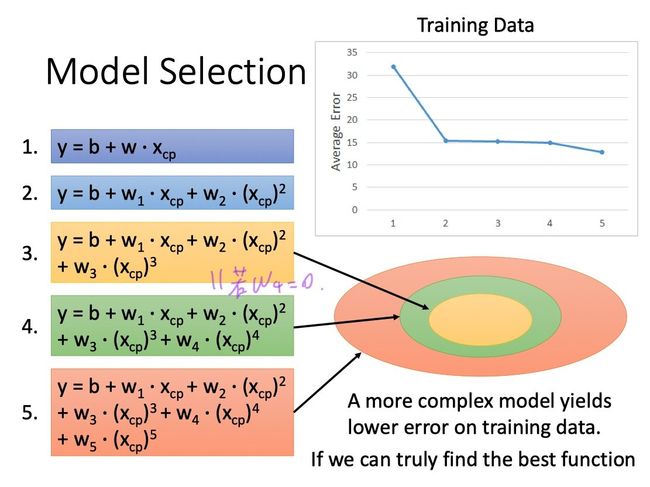
答:model越是复杂,由variance(方差)带来的error就可能更高,带来overfitting(过拟合)的情况(具体李宏毅老师下节课会有讲)
Back to Step1:Redesign the Model
当我们收集了更多data之后,发现宝可梦进化后的cp值明显存在某几种不同的模式,于是我们选择将更多的可能影响因素考虑进去(而不是仅考虑进化前的CP值),比如宝可梦种类,体重,生命值…

因此,我们需要重构Model
比如同时考虑宝可梦的CP值xcp和种类xs
-
当宝可梦是波波时,选择 y = b1 + w1 xcp
-
当宝可梦是独角虫时,选择 y = b2 + w2 xcp

如果要保证model是linear的,我们可以引入冲激函数δ。
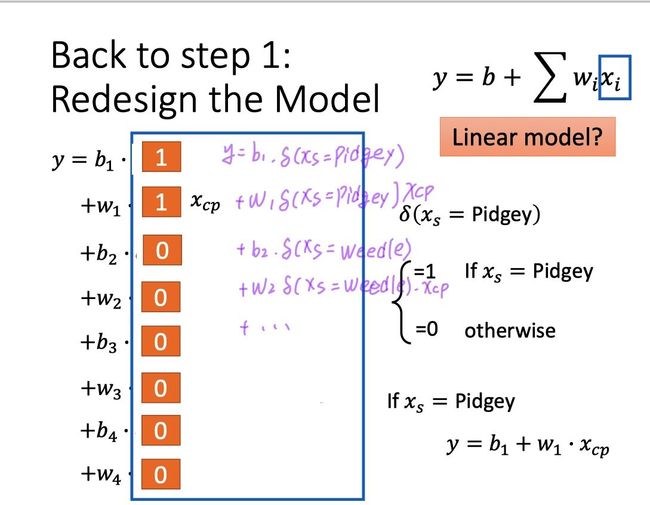
此时的测试结果如下

进一步,我们又可以Redesign the Model Again,例如引入二次项。当然了,结果不一定好,就像下面一样,又overfitting了!
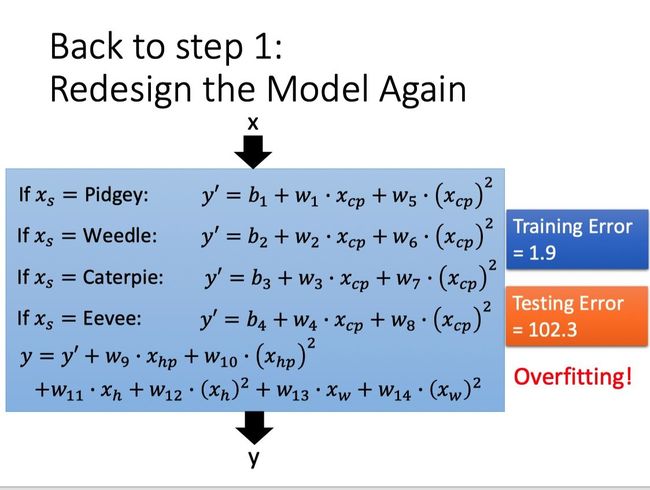
Back to Step2:Regularization
除了design the model以外我们还可以选择修改loss function,原来的loss function只考虑了预测值的error,即
L = ∑ n ( y ^ n − ( b + ∑ w i x i ) ) 2 L=\sum_{n}\left(\hat{y}^{n}-\left(b+\sum w_{i} x_{i}\right)\right)^{2} L=n∑(y^n−(b+∑wixi))2
现在在原来的基础上加上λΣ(wi)2,得到
L = ∑ n ( y ^ n − ( b + ∑ w i x i ) ) 2 + λ ∑ w i 2 L=\sum_{n}\left(\hat{y}^{n}-\left(b+\sum w_{i} x_{i}\right)\right)^{2} + λ \sum{w_i}^2 L=n∑(y^n−(b+∑wixi))2+λ∑wi2
在这里我们期望wi比较小,因为wi比较小的时候代表loss的曲线比较平滑,而loss曲线平滑意味着output受input的影响较小,也就是说这个output对input比较不sensitive,这时候output受noise的影响就比较小。
举例来说,对于y = b + Σwixi这个model,当input变化∆xi时,output变为y = b + Σwi(xi+∆xi),变化了Σwi∆xi。
当wi较小时,这种影响是微乎其微的。
在这里你会发现,我们做Regularization时并没有把bias(也就是b)这个参数考虑进去。原因是,bias的大小跟function(不是指loss function)的平滑程度是无关的,bias值的大小只是会把function曲线上下移动而已。

上文提到了我们喜欢比较平滑的function,因为它对noise不那么sensitive,但是我们又不期望function过于平滑,因为平滑的极限就是一条水平线,那么,它就失去了对data拟合的能力。
除了调整wi以外,我们还能调整λ的值来控制function的平滑程度。
λ值越大代表regularization那一项的影响力越大,我们找到的function就越平滑。
观察下图可知,当我们的λ越大的时候,在training data上得到的error其实是越大的,但是这件事情是非常合理的,因为当λ越大的时候,我们就越倾向于考虑w的值而越少考虑error的大小;但是有趣的是,虽然在training data上得到的error越大,但是在testing data上得到的error可能会是比较小的。
下图中,当λ从0到100变大的时候,training error不断变大,testing error反而不断变小。但是当λ太大(>100)的时候,在testing data上的error却又变得越来越大。
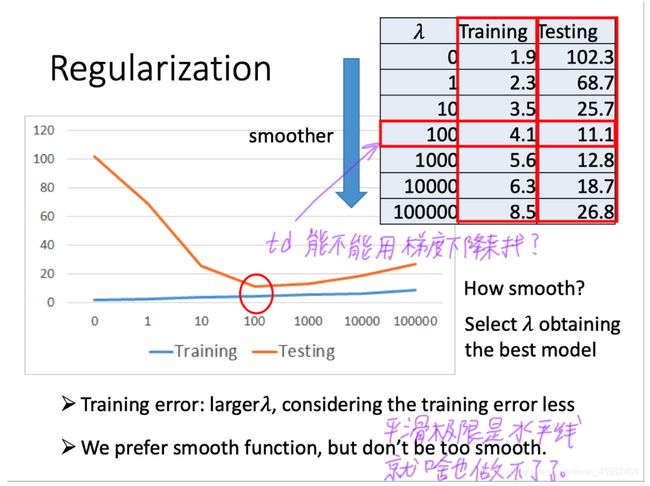
因此,选择合适的λ显得尤为重要。
在这里λ=100时,在testing data上的error最小,因此我们选择λ=100。
注:这里的error指的是 1 n ∑ i = 1 n ∣ y ^ i − y i ∣ \frac{1}{n} \sum_{i=1}^n \left| \hat{y}^i - y^i \right| n1∑i=1n∣∣y^i−yi∣∣
总结
-
Pokémon: Original CP and species almost decide the CP after evolution
- There are probably other hidden factors
-
Gradient descent
- More theory and tips in the following lectures Overfitting and Regularization
-
We finally get average error = 11.1 on the testing data
- How about new data? Larger error? Lower error?(larger->need validation)
-
Next lecture: Where does the error come from?
- More theory about overfitting and regularization
- The concept of validation。