复杂网络——多元时间序列转化网络
已经学习了一段时间有关复杂网络方面的资料。接下来想记录下自己一些心得体会。OK,let’go!
谈到复杂网络,首先不得避免谈到汪小凡的著作《2006_复杂网络理论及其应用 - 汪小帆》,这时一篇入门的为数不多的中文著作。这里给附上资源:
链接:https://pan.baidu.com/s/1p2VDdAgV29xgbqaenUBQ4A
提取码:2ass
OK,来简单讲述下自己最近所浏览的一篇论文《constructing ordinal partition transition networks from multivariate time series》中译为《从多元时间序列构造有序划分转换网络》
中英文PDF版资源如下:
链接:https://pan.baidu.com/s/1in4q7KQIhsUkUCwWzm3cGw
提取码:ecqi
接下来,让我们对照中文版的谈谈一些体会,在相应位置,有自己编写好的算法供大家参考
page one
已经提出了越来越多的算法来将标量时间序列映射到顺序分区转换网络中。 但是,经验科学中大多数可观察到的现象具有多元性质。 我们构建多元时间序列的序数分区转换网络。
这种方法产生了加权有向网络,该网络代表了速度空间中时间序列的模式转换特性,因此可以动态地了解下层系统。 此外,我们提出了一种熵的度量来表征有序分区过渡动力学,它对捕获相空间轨迹的可能局部几何变化很敏感。 我们证明了模式转换网络可用于捕获非相干转换的相位相干性,并表征相同步的路径。 因此,我们得出结论,有序分区过渡网络方法为非线性多元时间序列的传统符号分析提供了补充的见解。
非线性时间序列分析和复杂网络理论被广泛认为是与非线性动力学和统计物理学紧密联系的复杂系统科学领域。 越来越多的文献旨在利用复杂的网络方法来表征基于时间序列的动态系统。 有多种方法可以将给定的时间序列转换为网络表示形式,然后进行网络分析。 这里我们举几个典型的例子。 递归网络方法比较了相空间中时间点的接近性,这些时间点已应用于气候数据分析 [1、2],混沌电化学振荡器 [3],分数布朗运动4和油水两相过渡流动行为 [5-7]。
在音乐数据 [8] 中已经识别出一些基本的网络主题结构,其特征还在于修订的递归方法 [9]。 已经提出了一系列可见度图算法及其变体 [10-12],以通过计算两个采样点的每对之间的所谓线性可见度条件来转换给定的时间序列,这些条件已成功应用于美国的飓风数据 [13] ,金融市场 [14],黑子时间序列 [15、16],相关随机 [17] 和多重分形随机过程 [18],从复杂的系统角度提供了新颖的见解。 参考文献 [18、19和20] 中讨论了其他几种方法。例如,提出了循环网络的概念,用于将时间序列映射到网络 [21]。表征图案的顺序有助于区分高维混沌和低维混沌 [22]。此外,可以通过将时间序列的各段映射到可见性图并将连续状态链接到状态网络 [23、24] 来监视时间序列的演化行为。
最近,越来越多的工作通过时间序列的有序划分将时间序列转换为网络 [25、26]。在不规则采样的时间序列中进行了一系列有序方法的系统研究 [27-29] ,这显示了研究 来自气候科学的实验观测数据 [30] 。 在这种方法中,第一步是通过使用传统时延嵌入技术将一维时间序列嵌入相空间。 相空间中的十个嵌入式点被映射到网络空间中的节点,并且基于轨迹上的时间顺序在节点之间分配链接。 结果网络是相空间中时间序列的马尔可夫链表示。 网络分析的有趣之处在于,相当简单的网络测度(甚至包括平均度)也可以跟踪与最大Lyapunov指数相当的动态转变 [25] 。
page two
序数分区网络方法的基本思想可以追溯到识别时间序列 [31、32] 的序数模式。考虑一维时间序列{x(t)} t = 1,…,L包含来自a的L个点 动力学系统中,原始相空间可以通过时延嵌入x(t)= [x(t),x(t + τ),…,x(t +(Dx-1)τ)]来重建 Dx [33,34] .下一步是基于相对振幅计算x(t),x(t + τ),…,x(t +(Dx-1)τ)的等级顺序,方便地用 一个符号πx(t)。 当在嵌入空间中将窗口从t = 1滑动到N = L-(Dx-1)T时,会生成轨迹πx(t)的符号表示。 一种遵循符号表示法的传统方法是,基于阶数模式的频率图来计算置换熵,从而在非线性时间序列分析中产生非常完善的统计量 [31] 。 在最近的几十年中,时间序列的序数符号表示已在科学和工程中发现了许多有趣的应用,例如,生物医学记录 [35] ,金融 [36] ,气候科学 [37] 。 参考文献中对近期的一些进展进行了全面的回顾。 [35].但是,序数模式之间的过渡行为在很大程度上仍然不清楚。 最近的序数分区网络表示法捕获了序数模式的演化行为 [25、26] ,这为时间序列的标准序数符号分析提供了新颖的见解。
对于给定的嵌入尺寸Dx,总共有Dx! 可能会在时间序列中出现的唯一序数模式,而忽略了相等性。 平稳增量的随机过程满足P(xt = x.t + τ)= 0,因此具有联系xt = x.t + τ的概率为零。 对于经验时间序列,我们可以通过添加连续分布的微小白噪声来避免联系 [38] 。 因此,原始相空间将分解为Dx! 等效分区 [31] 。 所有Dx都很直观! 在N→∞的随机过程所产生的时间序列中,模式几乎以相等的频率出现。 但是,在确定性动力学产生的时间序列中,可能永远不会出现一组模式。 因此,可以通过对禁止模式进行计数来量化时间序列数据中的确定性。 然而,复杂性在实时分析中出现。 例如,缺失的序数模式可能与观察期间的有限时间长度以及相关的随机过程有关,这要求在相对较短的嘈杂数据中使用某些修订的方法来确定性的检测 [39-43] 。 从常规分区网络的角度来看,顺序模式的频率和不同模式之间的过渡都是不均匀的。 因此,如此获得的网络特性对不同的系统动力学很敏感,这可以成功地根据EEG数据 [25、26] 来表征健康与患者之间的差异。
最近的大多数工作都只关注单变量时间序列{x(t)}。 嵌入维数Dx和时间延迟T是构建有序分区网络的两个重要参数,尤其是对禁止顺序模式的出现具有关键影响 [27-29] 。 但是,对多元时间序列的泛化仍大体未触及 [5,44] 。经验科学中的大多数可观察到的现象都是多元性质的。 例如,同时观察股票市场中的资产,并分析其共同发展以更好地了解趋势。 在气候科学中,多种观测(温度,压力,降水,人类活动等,来自不同位置)是对未来气候状况进行可靠预测的基础。 我们建议从多元数据构建有序分区转换网络。
顺序模式定义 给定由确定性动态系统生成的标量时间序列{x(t)},时间序列的顺序结构取决于嵌入维Dx和时间延迟τ [33、34]。
让我们从Dx = 2开始。 忽略相等,我们在x(t)和x(t +τ)之间有两个关系,即代表顺序模式πx的两个符号序列:

对于具有连续分布值的动力系统,我们可以忽略相等性,因为Lebesgue对关系的测度为零 [31] 。 此外,大量的数值模拟表明结果不会发生质的变化,并且我们对x(t)
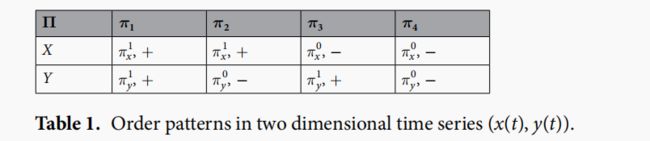
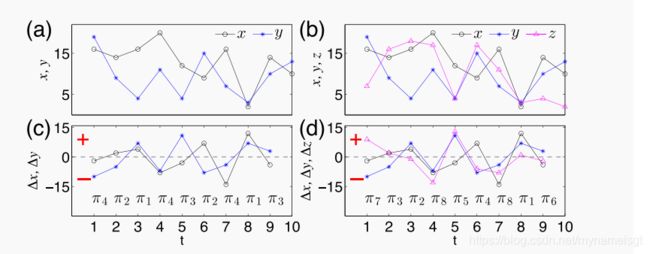
当将上述思想推广到二维时间序列(x(t),y(t))时,我们将讨论局限于将Dx = Dy = 2嵌入到单个变量中。 因此,根据递增符号(Δx(t),Δy(t))(表1),我们有四种不同的顺序模式组合:在(x(t),y(t))的相空间中,我们 具有阶式Π(t)∈(π1,π2,π3,π4)捕获了递增或递减的行为。 图 1(a,c) 的示例显示了二维序列(x(t),y(t))的有序模式的构造。 完全类推,基于增量(Δx(t),Δy(t),Δz(t)),序数模式TT(t)属于(Π1,…,Πi)i = 1,…,8 表 [2] 列举了三维时间序列(x(t),y(t),z(t))的坐标,并在图**1(b,d)**中将其可视化。 因此,n维时间序列({x1}(t),…,{xn}(t))的阶模Π(t)的维数为D = 2 ^ n,因为每个分量要么增加要么降低在时间t下降趋势。
page three
图1.(a)二维序列(x(t),y(t))和(c)增量序列(Δx(t),Δy(t))的阶序模式定义。 (b)树的维数级数(x(t),y(t),z(t))和(d)相应的增量级数(Δx(t),Δy(t),Δy(t))。 (c,d)分别表示增量级数和序号的符号
提供代码如下:
%% 二维时间序列模式
clear;clc
%初始数据
n=10; %%时间序列长度为10
m=20; %%大小设定为20之内
x=m*rand(1,n); %%随机生成长度为10的x的时间序列,大小在0~20
y=m*rand(1,n); %%随机生成长度为10的y的时间序列,大小在0~20
delta_x=diff(x); %%求x的差分,此时周期为1
delta_y=diff(y); %%求y的差分,此时周期为1
m=length(delta_x); %%获得差分长度
%--------------------------------------------------------------------------
%记录π序数
pai_xushu=cell(1,m);
for i=1:m %%得到m个π序数
if delta_x(i)>=0 && delta_y(i)>=0
pai_xushu{
i}='π1';
elseif delta_x(i)>=0 && delta_y(i)<0
pai_xushu{
i}='π2';
elseif delta_x(i)<0 && delta_y(i)>=0
pai_xushu{
i}='π3';
else
pai_xushu{
i}='π4';
end
end
%绘图区
i=1:n; %%画生成x,y图对应需要
j=1:n-1; %%画差分增量模式图需要
figure(1);
subplot(2,1,1);
plot(i,x,'o-');hold on;plot(i,y,'b*-');hold off;
ylabel('x,y');
h1=legend('x','y'); %%设置图例
set(h1,'Orientation','horizon');
set(h1,'Box','off');
subplot(2,1,2);
plot(j,delta_x,'o-');hold on;plot(j,delta_y,'b*-');hold off;
line([0,n],[0,0],'linestyle','--'); %%添加横坐标0-n,纵坐标0-0的虚线
for i=1:n-1
text(i,0,pai_xushu(i)); %%显示对应结果的π模式
end
xlabel('t');
ylabel('Δx,Δy');
h2=legend('Δx','Δy'); %%设置图例
set(h2,'Orientation','horizon');
set(h2,'Box','off');
%% 三维时间序列
clear;clc
%初始数据
n=10; %%时间序列长度为10
m=20; %%大小设定为20之内
x=m*rand(1,n); %%随机生成长度为10的x的时间序列,大小在0~20
y=m*rand(1,n); %%随机生成长度为10的y的时间序列,大小在0~20
z=m*rand(1,n); %%随机生成长度为10的z的时间序列,大小在0~20
delta_x=diff(x); %%求x的差分
delta_y=diff(y); %%求y的差分
delta_z=diff(z); %%求z的差分
m=length(delta_x);
%记录π序数
pai_xushu=cell(1,m);
for i=1:m %%得到n-1个π序数
if delta_x(i)>=0 && delta_y(i)>=0 && delta_z(i)>=0
pai_xushu{
i}='π1';
elseif delta_x(i)>=0 && delta_y(i)>=0 && delta_z(i)<0
pai_xushu{
i}='π2';
elseif delta_x(i)>=0 && delta_y(i)<0 && delta_z(i)>=0
pai_xushu{
i}='π3';
elseif delta_x(i)>=0 && delta_y(i)<0 && delta_z(i)<0
pai_xushu{
i}='π4';
elseif delta_x(i)<0 && delta_y(i)>=0 && delta_z(i)>=0
pai_xushu{
i}='π5';
elseif delta_x(i)<0 && delta_y(i)>=0 && delta_z(i)<0
pai_xushu{
i}='π6';
elseif delta_x(i)<0 && delta_y(i)<0 && delta_z(i)>=0
pai_xushu{
i}='π7';
else
pai_xushu{
i}='π8';
end
end
%绘图区
i=1:n; %%画生成x,y图对应需要
j=1:n-1; %%画差分增量模式图需要
figure(1);
subplot(2,1,1);
plot(i,x,'o-');hold on;plot(i,y,'b*-');hold on;plot(i,z,'m^-');hold off;
ylabel('x,y,z');
h1=legend('x','y','z'); %%设置图例
set(h1,'Orientation','horizon');
set(h1,'Box','off');
subplot(2,1,2);
plot(j,delta_x,'o-');hold on;plot(j,delta_y,'b*-');hold on;plot(j,delta_z,'m^-');hold off;
line([0,n],[0,0],'linestyle','--'); %%添加横坐标0-n,纵坐标0-0的虚线
for i=1:n-1
text(i,0,pai_xushu(i)); %%显示对应结果的π模式
end
xlabel('t');
ylabel('Δx,Δy,Δz');
h2=legend('Δx','Δy','Δz'); %%设置图例
set(h2,'Orientation','horizon');
set(h2,'Box','off')
运行结果为:
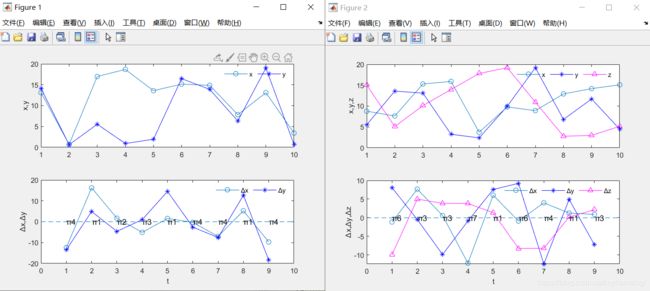
因为我是随机生成的时间序列,所以图片会有差异,但已基本实现要求
注意,在这项工作中,我们没有应用时间延迟嵌入技术来从一个单变量时间序列获得多维相空间。 相反,在给定多元时间序列的情况下,我们考虑在多重测量空间中每个测量的两个连续时间点之间的增量。 换句话说,我们的方法在与其相关的速度空间(差异空间)中捕获了多元时间序列的动态特性。 因此,顺序模式定义(公式 (1) )中的时间延迟τ与嵌入中经常使用的时间延迟具有不同的解释。 传统上,一个适当地选一个嵌入丁维和时间延迟来重建相空间从一个给定的单变量的时间序列。 我们当然可以将讨论推广到以下情况:时间延迟大于1(即τ> 1),并且对于每个变量(度量)都嵌入维度Dx> 2,但是我们认为对于多变量而言,动力学方面的物理意义变得模棱两可 时间序列。
顺序分区转换网络。 给定一个多元时间序列,例如(x(t),y(t))的二维情况,我们将第i个模式πi的频率表示为p(πi) 时间间隔t = 1,…,N。 一个重要的特性是确定性过程中的序数模式具有不同的频率p(πi)。 然后引入置换熵HO来表征序数模式的不均匀外观,如下所示

其中总和遍历所有D = 2 ^ n个排列。 我们使用log2,因此HO的单位是位。 对于一个n维独立的相同分布式随机过程,由于每个D = 2 ^ n序数模式都具有相同的频率,因此可以获得最大的熵HO = n。
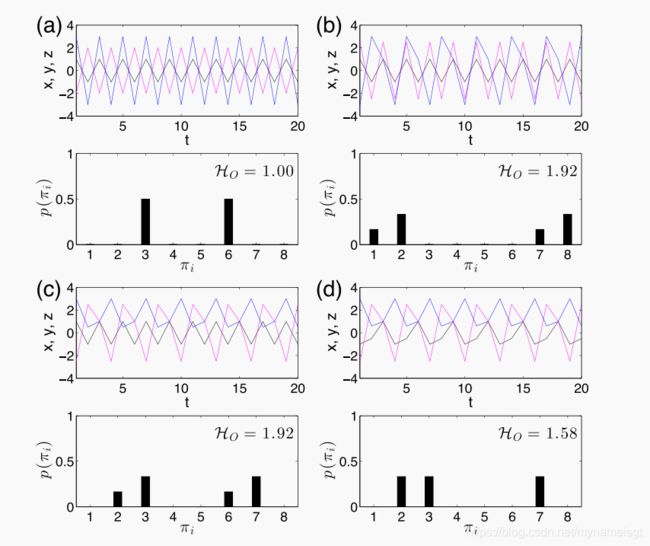
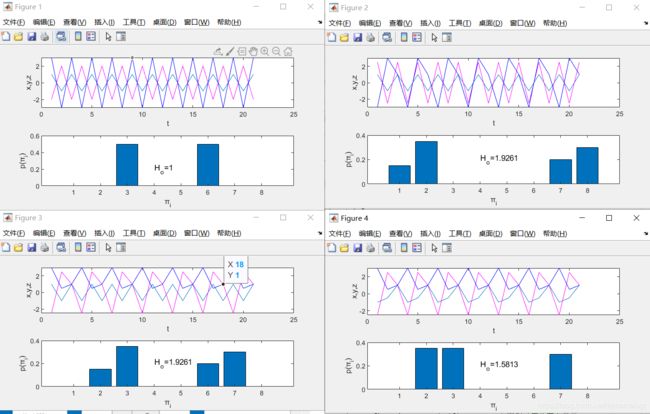
我们通过使用图2中的三维相同的独立周期序列的玩具模型来说明上述算法.3D周期序列的周期的不同组合会产生置换熵HO的不同值。 此外,广泛观察到有限数量的可能的序数模式(禁止的模式),从而影响了该系列的确定性。
当前的大多数研究都集中在考虑顺序模式的频率来计算置换熵HO上,该方法并未揭示顺序模式之间的过渡行为。 因此,HO是静态的。 例如,仅在HO值为1.92的情况下,图 2(b,c) 中的动力学细节仍然不清楚,因为HO并未公开(c)中图 2(b) 的独特过渡特性。 从可视化的角度来看,图 3(a,b) 中方便地显示了阶跃模式之间的过渡差异。
page four
图2.周期性3D序列(x(t),y(t),z(t))的玩具模型及其相关的订购模式直方图。
(a)x(t),y(t)和z(t)的周期为2。(b)x(t)和y(t)的周期为2,而z(t)的周期为3。 c)x(t)的周期为2,y(t)和z(t)的周期为3。(d)x(t),y(t)和z(t)的周期为3。各自的频率曲线 时间序列下方显示了序数模式的变化,图例中显示了熵值HO
提供代码如下:
clear;clc
%a组初始数据,x,y,z周期为2
% x=[1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1];
% y=[-2 2 -2 2 -2 2 -2 2 -2 2 -2 2 -2 2 -2 2 -2 2 -2 2 -2];
% z=[3 -3 3 -3 3 -3 3 -3 3 -3 3 -3 3 -3 3 -3 3 -3 3 -3 3];
%b组初始数据,x,y周期为2,z周期为3
% x=[1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1];
% y=[2.5 -2.5 2.5 -2.5 2.5 -2.5 2.5 -2.5 2.5 -2.5 2.5 -2.5 2.5 -2.5 2.5 -2.5 2.5 -2.5 2.5 -2.5 2.5];
% z=[-3 3 1 -3 3 1 -3 3 1 -3 3 1 -3 3 1 -3 3 1 -3 3 1];
% %c组初始数据,x周期为2,y、z周期为3
% x=[1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1];
% y=[-2.5 2.5 1 -2.5 2.5 1 -2.5 2.5 1 -2.5 2.5 1 -2.5 2.5 1 -2.5 2.5 1 -2.5 2.5 1];
% z=[3 0.5 1 3 0.5 1 3 0.5 1 3 0.5 1 3 0.5 1 3 0.5 1 3 0.5 1];
% %d组初始数据,x、y、z周期为3
% x=[-1 -0.5 1 -1 -0.5 1 -1 -0.5 1 -1 -0.5 1 -1 -0.5 1 -1 -0.5 1 -1 -0.5 1];
% y=[-2.5 2.5 1 -2.5 2.5 1 -2.5 2.5 1 -2.5 2.5 1 -2.5 2.5 1 -2.5 2.5 1 -2.5 2.5 1];
% z=[3 0.5 1 3 0.5 1 3 0.5 1 3 0.5 1 3 0.5 1 3 0.5 1 3 0.5 1];
n=length(x); %%获取原始时间序列的长度
delta_x=diff(x); %%求x的差分
delta_y=diff(y); %%求y的差分
delta_z=diff(z); %%求z的差分
m=length(delta_x); %%获得差分长度
%--------------------------------------------------------------------------
%记录π序数
pai_xushu=cell(1,m); %%直观显示对应的π模式
digit_xushu=zeros(1,m); %%编程序简易,以1->π1,2->π2,…,n->πn
for i=1:m %%得到m个π序数
if delta_x(i)>=0 && delta_y(i)>=0 && delta_z(i)>=0
pai_xushu{
i}='π1';
digit_xushu(i)=1;
elseif delta_x(i)>=0 && delta_y(i)>=0 && delta_z(i)<0
pai_xushu{
i}='π2';
digit_xushu(i)=2;
elseif delta_x(i)>=0 && delta_y(i)<0 && delta_z(i)>=0
pai_xushu{
i}='π3';
digit_xushu(i)=3;
elseif delta_x(i)>=0 && delta_y(i)<0 && delta_z(i)<0
pai_xushu{
i}='π4';
digit_xushu(i)=4;
elseif delta_x(i)<0 && delta_y(i)>=0 && delta_z(i)>=0
pai_xushu{
i}='π5';
digit_xushu(i)=5;
elseif delta_x(i)<0 && delta_y(i)>=0 && delta_z(i)<0
pai_xushu{
i}='π6';
digit_xushu(i)=6;
elseif delta_x(i)<0 && delta_y(i)<0 && delta_z(i)>=0
pai_xushu{
i}='π7';
digit_xushu(i)=7;
else
pai_xushu{
i}='π8';
digit_xushu(i)=8;
end
end
%记录π模式概率p(πi)及其相应的熵值Ho
pai_count=zeros(1,8);
for i=1:m
for j=1:8
if digit_xushu(i)==j
pai_count(j)=pai_count(j)+1; %%记录对应的πi出现的个数
end
end
end
P=pai_count/sum(pai_count); %%获得每个πi占总体的比例
Ho=0;
for j=1:8
if P(j)~=0
Ho=Ho-P(j)*log2(P(j));
end
end
%绘图区
i=1:n; %%画生成x、y、z图对应需要x轴
j=1:m; %%画差分增量模式图需要x轴
figure(1);
subplot(2,1,1);
plot(i,x,'-');hold on;plot(i,y,'m-');hold on;plot(i,z,'b-');hold off;
xlabel('t');ylabel('x,y,z');
subplot(2,1,2);
bar(P); %%画直方图
xlabel('π_i');ylabel('p(π_i)');
text(4,0.2,['H_o=' num2str(Ho)]); %%在图形对应位置上显示πi
结果如下:
与3维不相关的独立相同的分布随机均匀噪声相比,有序分区网络是一个完整的连接图(图3(c))。 另外,在序列的时间迭代之后,我们通过其过渡频率wij = p(πi→πj)指示每个有向链路。 最后,我们得出一个加权有向网络,其特征在于加权邻接矩阵W = {wij},i,j∈[1,2 ^ n]。 矩阵W满足归一化∑ i,j-> 2 ^ n wij = 1。 在此,基于W,通过香农熵HT量化有序模式转换特性的规律性,即
总和遍及所有可能的2 ^ 2n转换。 完全类似于HO,对于一个n维独立的相同分布随机过程,可以获得最大熵HT = 2n。
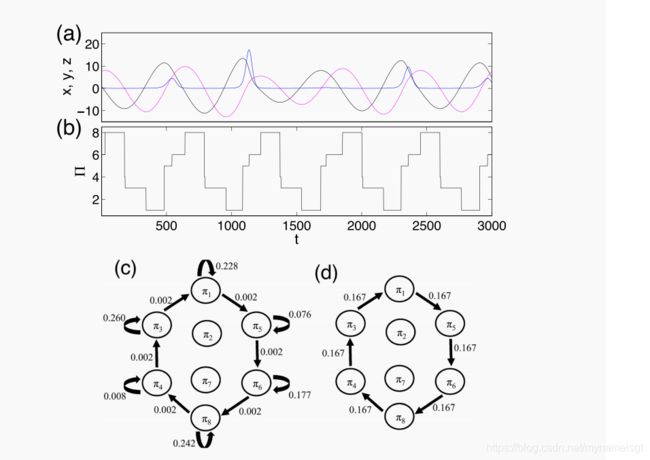
对于由随机过程产生的时间序列,计算HT相当简单。 但是,我们需要注意连续系统的情况,该系统在生成的网络中会产生较大比例的自环,如下所示。 这里我们以混沌的Rössler系统为例
其中a = 0.165,ω= 1.0。 公式 (4) 通过四阶Runge Kutta方法进行数值积分,积分步骤h = 0.01。 丢弃前10000个瞬态数据点,并分析由N = 500000个数据点组成的时间序列。 时间序列的短段(x,y,z)如图 4(a) 所示。 由于系统的连续性,在某些时间间隔内有许多高原会影响顺序模式的不变性(图 4(b) )。 这些高原通过最终的过渡网络中的自环来完成(图 4(c) )。 在现有的大多数复杂网络研究中,由于计算简单和理论上的考虑,都避免了自环 [46] 。 在Rössler系统的情况下,大约有99%的自环,而只有大约1%的非自环(如图 4(c) 中的箭头所示)。
page five
图3.(a)分别用于图 2(b) 的周期性过程的序数分区过渡网络,(b)用于图 2(c) 。 面板(c)对应于3D独立的相同分布随机均匀噪声,其中链接箭头(双向)被抑制以便于可视化。
图4.混沌Rössler系统(a = 0.165):(a)时间序列的短段(x,y,z),(b)与(a,c)顺序模式的特定时间窗口相对应的顺序模式的时间变化 有自环的跃迁网络,HO = 2.283,(d)没有自环的跃迁网络,HT = 2.585,其中观察到过渡路径π1→π5→π6→π8→π4→π3→π1。 链接上的值表示顺序模式的相应转换频率。 注意,在获得(c,d)中使用了N = 500000个数据点。
提供代码如下:
%%混Rossler系统-公式,四阶Runge Kutta方法 历时 16.848760 秒。
%初始数据
clear;clc
tic
global w %%定义全局变量w
global a; %%定义全局变量a
N=500000;h=0.01; %%迭代N次,步长h;
w=1.0;a=0.165; %%设定w,a
x=zeros(1,N);y=zeros(1,N);z=zeros(1,N); %%提前分配内存空间
x(1)=0;y(1)=8;z(1)=0.5; %%设定初始点
%四阶Runge-Kutta算法
for i=1:N
x_k1=f_dx(y(i),z(i)); %%调用自编写f_dx函数
y_k1=f_dy(x(i),y(i)); %%调用自编写f_dy函数
z_k1=f_dz(x(i),z(i)); %%调用自编写f_dz函数
x_k2=f_dx(y(i)+h/2*y_k1,z(i)+h/2*z_k1);
y_k2=f_dy(x(i)+h/2*x_k1,y(i)+h/2*y_k1);
z_k2=f_dz(x(i)+h/2*x_k1,z(i)+h/2*z_k1);
x_k3=f_dx(y(i)+h/2*y_k2,z(i)+h/2*z_k2);
y_k3=f_dy(x(i)+h/2*x_k2,y(i)+h/2*y_k2);
z_k3=f_dz(x(i)+h/2*x_k1,z(i)+h/2*z_k2);
x_k4=f_dx(y(i)+h*y_k3,z(i)+h*z_k3);
y_k4=f_dy(x(i)+h*x_k3,y(i)+h*y_k3);
z_k4=f_dz(x(i)+h*x_k3,z(i)+h*z_k3);
x(i+1)=x(i)+h/6*(x_k1+2*x_k2+2*x_k3+x_k4);
y(i+1)=y(i)+h/6*(y_k1+2*y_k2+2*y_k3+y_k4);
z(i+1)=z(i)+h/6*(z_k1+2*z_k2+2*z_k3+z_k4);
end
%获得x,y,z序列后进行差分
delta_x=diff(x); %%对余下的x序列进行差分
delta_y=diff(y); %%对余下的y序列进行差分
delta_z=diff(z); %%对余下的z序列进行差分
m=length(delta_x); %%获取余下的x序列长度
%记录π序数
pai_xushu=cell(1,m); %%直观显示对应的π模式
digit_xushu=zeros(1,m); %%编程序简易,以1->π1,2->π2,…,n->πn
for i=1:m %%得到m个π序数
if delta_x(i)>=0 && delta_y(i)>=0 && delta_z(i)>=0
pai_xushu{
i}='π1';
digit_xushu(i)=1;
elseif delta_x(i)>=0 && delta_y(i)>=0 && delta_z(i)<0
pai_xushu{
i}='π2';
digit_xushu(i)=2;
elseif delta_x(i)>=0 && delta_y(i)<0 && delta_z(i)>=0
pai_xushu{
i}='π3';
digit_xushu(i)=3;
elseif delta_x(i)>=0 && delta_y(i)<0 && delta_z(i)<0
pai_xushu{
i}='π4';
digit_xushu(i)=4;
elseif delta_x(i)<0 && delta_y(i)>=0 && delta_z(i)>=0
pai_xushu{
i}='π5';
digit_xushu(i)=5;
elseif delta_x(i)<0 && delta_y(i)>=0 && delta_z(i)<0
pai_xushu{
i}='π6';
digit_xushu(i)=6;
elseif delta_x(i)<0 && delta_y(i)<0 && delta_z(i)>=0
pai_xushu{
i}='π7';
digit_xushu(i)=7;
else
pai_xushu{
i}='π8';
digit_xushu(i)=8;
end
end
%丢失前clear_N个数据点
clear_N=10000; %%设定丢弃数据点
x_clear=x(1:clear_N);x(1:clear_N)=[]; %%x前clear_N个数据点存入x_clear
y_clear=y(1:clear_N);y(1:clear_N)=[]; %%y前clear_N个数据点存入y_clear
z_clear=z(1:clear_N);z(1:clear_N)=[]; %%z前clear_N个数据点存入z_clear
digit_xushu_clear_N=digit_xushu(1:clear_N);digit_xushu(1:clear_N)=[];
m=length(digit_xushu);
%计算记录π模式概率p(πi)及其相应的熵值Ho
pai_count=zeros(1,8);
for i=1:m
for j=1:8
if digit_xushu(i) == j
pai_count(j)=pai_count(j)+1; %%记录对应πi出现的个数
end
end
end
P=pai_count/sum(pai_count); %%获得每个πi占总体的比例
Ho=0;
P(find(P==0))=1; %%消除概率为0取歧义对数的情况,log2(1)=0,不影响最后熵值结果
for j=1:8
Ho=Ho-P(j)*log2(P(j));
end
P(find(P==1))=0; %%复原
disp('π模式出现的概率及其对应的熵Ho');
for i=1:8
if P(i)~=0
disp(['π' num2str(i) ' is ' num2str(P(i))]); %%控制台上显示单个πi对应的概率
end
end
Ho
disp('---------------------------------------------');
%计算π模式的转化概率以及HT
pai_ij_count=zeros(8,8);
for k=1:m-1
for i=1:8
for j=1:8
if digit_xushu(k) == i && digit_xushu(k+1) == j %%如果第k个π模式为πi,第k+1个π模式为πj
pai_ij_count(i,j)=pai_ij_count(i,j)+1; %%则在第i行第j列+1。最后可得到转移数量矩阵。
end
end
end
end
P_ij=pai_ij_count/sum(sum(pai_ij_count)); %%获得每个πi->πj的转移概率
P_ij(find(P_ij==0))=1; %%消除概率为0取歧义对数的情况,log2(1)=0,不影响最后熵值结果
HT=0;
for i=1:8
for j=1:8
HT=HT-P_ij(i,j)*log2(P_ij(i,j));
end
end
P_ij(find(P_ij==1))=0; %%复原
disp("π模式传递概率及相应的HT")
for i=1:8
for j=1:8
if P_ij(i,j)~=0
disp(['π' num2str(i) '->' 'π' num2str(j) ' is ' num2str(P_ij(i,j))] ) %%在控制台显示πi->πj的转移概率
end
end
end
HT
disp('---------------------------------------------------------------------')
%去除自环后的概率及Ht
pai_ij_count_2=pai_ij_count-diag(diag(pai_ij_count)); %%对角线置0,去除自环现象
P_ij_2=pai_ij_count_2/sum(sum(pai_ij_count_2)); %%余下进行归一化得其转移概率
P_ij_2(find(P_ij_2==0))=1; %%消除概率为0取歧义对数的情况,log2(1)=0,不影响最后熵值结果
HT_2=0;
for i=1:8
for j=1:8
HT_2=HT_2-P_ij_2(i,j)*log2(P_ij_2(i,j));
end
end
P_ij_2(find(P_ij_2==1))=0; %%复原
disp("去除自环后,π模式传递概率及相应的HT_2")
for i=1:8
for j=1:8
if P_ij_2(i,j)~=0
disp(['π' num2str(i) '->' 'π' num2str(j) ' is ' num2str(P_ij_2(i,j))] ) %%在控制台显示πi->πj(i~=j)的转移概率
end
end
end
HT_2
%%绘图区
figure(1);
n=3000; %%短段,长度为n
i=1:n; %%画图所需对应x轴
subplot(2,1,1);
plot(i,x_clear(i),'-');hold on;plot(i,y_clear(i),'m-');hold on;plot(i,z_clear(i),'b-');hold off;
ylabel('x,y,z');title('(a)');
h1=legend('x','y','z'); %%设置图例
set(h1,'Orientation','horizon');
set(h1,'Box','off');
subplot(2,1,2);
i=1:n;
plot(i,digit_xushu_clear_N(i),'-');
xlabel('t');ylabel('π');title('(b)');
figure(2)
for i=1:8
L(i)=length(find(digit_xushu==i)); %%得到出现πi的个数
end
for i=1:8
index(i,1:L(i))=find(digit_xushu==i); %%πi对应在序列中的位置,方便作图
end
plot3(x(index(1,1:L(1))),y(index(1,1:L(1))),z(index(1,1:L(1))),'c*');hold on;
plot3(x(index(2,1:L(2))),y(index(2,1:L(2))),z(index(2,1:L(2))),'r*');hold on;
plot3(x(index(3,1:L(3))),y(index(3,1:L(3))),z(index(3,1:L(3))),'y*');hold on;
plot3(x(index(4,1:L(4))),y(index(4,1:L(4))),z(index(4,1:L(4))),'k*');hold on;
plot3(x(index(5,1:L(5))),y(index(5,1:L(5))),z(index(5,1:L(5))),'m*');hold on;
plot3(x(index(6,1:L(6))),y(index(6,1:L(6))),z(index(6,1:L(6))),'b*');hold on;
plot3(x(index(7,1:L(7))),y(index(7,1:L(7))),z(index(7,1:L(7))),'k*');hold on;
plot3(x(index(8,1:L(8))),y(index(8,1:L(8))),z(index(8,1:L(8))),'g*');hold off;
h1=legend('π_1','π2','π_3','π_4','π_5','π_6','π_8'); %%设置图例
set(h1,'Box','off');
toc
%由公式4所得函数
function f=f_dx(y,z) %%dx/dt
global w
f=-w*y-z;
end
function f=f_dy(x,y) %%dy/dt
global w
global a
f=w*x+a*y;
end
function f=f_dz(x,z) %%dz/dt
f=0.4+z*(x-8.5);
end
结果如下:
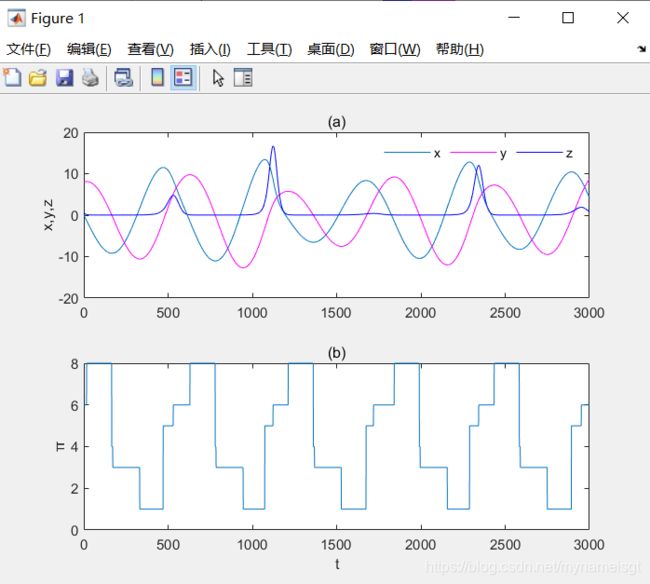
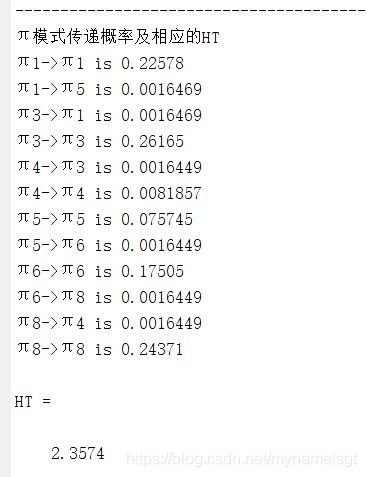
基本达到了原文献的要求~ 上面的代码也会顺应求出图六的图形,图四、六用的都是同一个混沌Rossler系统
page six
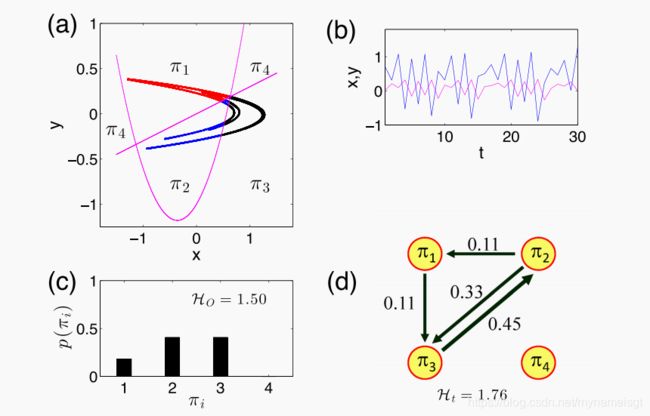
图5.Hénon映射:(a)吸引子,(b)时间序列的分段,(c)顺序模式的直方图导致HO =1.5和(d)顺序模式转换网络去除了自环,从而产生HT = 1.76。
提供代码如下:
%初始数据
clear;clc
n=30; %%设定时间序列长度
x=zeros(1,n);y=zeros(1,n);
x(1)=0.76;y(1)=0; %%设定初值
for i=2:n %%迭代得到完整的序列值
x(i)=y(i-1)+1-1.4*x(i-1)^2;
y(i)=0.3*x(i-1);
end
delta_x=diff(x); %%求x的差分
delta_y=diff(y); %%求y的差分
m=length(delta_x); %%获取差分长度
%记录π序数
pai_xushu=cell(1,m); %%直观显示对应的π模式
digit_xushu=zeros(1,m); %%编程序简易,以1->π1,2->π2,…,n->πn
for i=1:m %%得到m个π序数
if delta_x(i)>=0 && delta_y(i)>=0
pai_xushu{
i}='π1';
digit_xushu(i)=1;
elseif delta_x(i)>=0 && delta_y(i)<0
pai_xushu{
i}='π2';
digit_xushu(i)=2;
elseif delta_x(i)<0 && delta_y(i)>=0
pai_xushu{
i}='π3';
digit_xushu(i)=3;
else
pai_xushu{
i}='π4';
digit_xushu(i)=4;
end
end
pai_count=zeros(1,4);
for i=1:m
for j=1:4
if digit_xushu(i)==j
pai_count(j)=pai_count(j)+1; %%记录对应πi出现的个数
end
end
end
P=pai_count/sum(pai_count); %%获得每个πi占总体的比例
Ho=0;
P(find(P==0))=1; %%消除概率为0取歧义对数的情况,log2(1)=0,不影响最后熵值结果
for j=1:4
Ho=Ho-P(j)*log2(P(j));
end
P(find(P==1))=0; %%复原
%计算π模式转移概率
pai_ij_count=zeros(4,4);
for k=1:m-1
for i=1:4
for j=1:4
if digit_xushu(k) == i && digit_xushu(k+1) == j %%如果第k个π模式为πi,第k+1个π模式为πj
pai_ij_count(i,j)=pai_ij_count(i,j)+1; %%则在i行j列+1。最后可得到转移数量矩阵。
end
end
end
end
P_ij=pai_ij_count/sum(sum(pai_ij_count)); %%获得每个πi->πj的转移概率
P_ij(find(P_ij==0))=1; %%消除概率为0取歧义对数的情况,log2(1)=0,不影响最后熵值结果
HT=0;
for i=1:4
for j=1:4
HT=HT-P_ij(i,j)*log2(P_ij(i,j));
end
end
P_ij(find(P_ij==1))=0; %%复原
disp("未去除自环时的概率矩阵P_ij及相应的HT")
P_ij,HT
for i=1:4
for j=1:4
if P_ij(i,j)~=0
disp(['π' num2str(i) '->' 'π' num2str(j) ' is ' num2str(P_ij(i,j))] ) %%在控制台显示
end
end
end
disp('---------------------------------------------------------------------')
%去除自环后的概率pai_ij_count_2及Ht_2
pai_ij_count_2=pai_ij_count-diag(diag(pai_ij_count)); %%对角线置0,去除自环现象
P_ij_2=pai_ij_count_2/sum(sum(pai_ij_count_2)); %%余下进行归一化得其转移概率
P_ij_2(find(P_ij_2==0))=1; %%消除概率为0取歧义对数的情况,log2(1)=0,不影响最后熵值结果
HT_2=0;
for i=1:4
for j=1:4
HT_2=HT_2-P_ij_2(i,j)*log2(P_ij_2(i,j));
end
end
P_ij_2(find(P_ij_2==1))=0; %复原
disp("去除自环时的概率矩阵P_ij_2及相应的HT_2")
P_ij_2,HT_2
for i=1:4
for j=1:4
if P_ij_2(i,j)~=0
disp(['π' num2str(i) '->' 'π' num2str(j) ' is ' num2str(P_ij_2(i,j))] ) %%在控制台显示
end
end
end
%%绘图区
figure(1);
%图a
subplot(2,2,1);
x1=-1.5:0.01:1.5;y1=1.4*x1.^2+x1-1; %%L1
x2=-1.5:0.01:1.5;y2=0.3*x2; %%L2
plot(x1,y1,'m-');hold on;plot(x2,y2,'m-');hold on;
xlabel('x');ylabel('y');
title('(a)')
for i=1:4
L(i)=length(find(digit_xushu==i));
end
for i=1:4
index(i,1:L(i))=find(digit_xushu==i);
end
plot(x(index(1,1:L(1))),y(index(1,1:L(1))),'b*');hold on;plot(x(index(2,1:L(2))),y(index(2,1:L(2))),'r*');hold on;
plot(x(index(3,1:L(3))),y(index(3,1:L(3))),'*');hold on;plot(x(index(4,1:L(4))),y(index(4,1:L(4))),'m*');hold off;
%图b
subplot(2,2,2);
i=1:n; %%画生成x、y对应的图需x轴
plot(i,x,'-');hold on;plot(i,y,'m-');hold on;hold off;
xlabel('t');ylabel('x,y');
title('b');
h1=legend('x','y'); %%设置图例格式
set(h1,'Orientation','horizon');
set(h1,'Box','off');
%图c
subplot(2,2,3);
bar(P);
xlabel('π_i');ylabel('p(π_i)');
title('c');
text(3.3,0.3,['H_o=' num2str(Ho)]); %%在图形对应位置上显示H_o
结果如下:


我选取的时间序列长度为30,基本达到了文献要求的结果
加权邻接矩阵W可以分为对角和非对角项。 考虑到数值观察结果,W(自环)的对角元素远大于非对角元素Eq(3)简化为
因此,当考虑到自环时,我们得到一个连续系统的HT≈HO。 在这种情况下,HT很难捕获不同顺序模式之间的过渡。
为了强调序数模式之间非自我过渡的重要性,我们通过将W中的对角线值设置为0来移除如图 4(d) 所示的自环。这是大多数关于复数的研究工作的典型 网络 [46] 。 此外,我们在计算加权矩阵W之前删除自环,以保持标准化∑i,j-> 2 ^ n wij = 1。 请注意,在随机过程中不应期望大量的自循环
相空间的序数模式分区。 顺序模式转换网络为我们提供了相空间分区的替代方案,该方案利用了系统的零线。 在这里,我们显示了两个涉及离散和连续动力系统的示例。
示例(1):Hénon地图
选择作为一个混沌二维地图的示例。 吸引子的顺序模式分区如图 5(a) 所示,按不同的顺序模式进行颜色编码。 时间序列的一部分如图 5(b) 所示。阶数模式的直方图(图 5(c) )发现π4是系统的禁止模式,其HO = 1.50。 相应的序数分区过渡网络如图 5(d) 所示,每条链路的频率以雾度表示,得出HT = 1.76。
page seven
图6.(a)相序颜色编码的相空间中的Rössler吸引子(a = 0.165),由图例表示。 没有观察到模式π2和π7。 (b)上图是变量x,y和z之间的激活-抑制关系,其中激活用普通箭头表示,而抑制用禁止箭头47表示; 下面板代表系统所有允许的(不一定要观察到的)模式转换。 相应的顺序分区转换网络如图4**(d)**所示。 面板(c)与(a)的a = 0.26相同,其中突出显示了大量π2模式,(d)是有序分区转换网络(不包括自环),其中从π4进行了替代转换 →观察到π2→π1
代码见图4那里,这里附上跑出来的图
a=0.165时
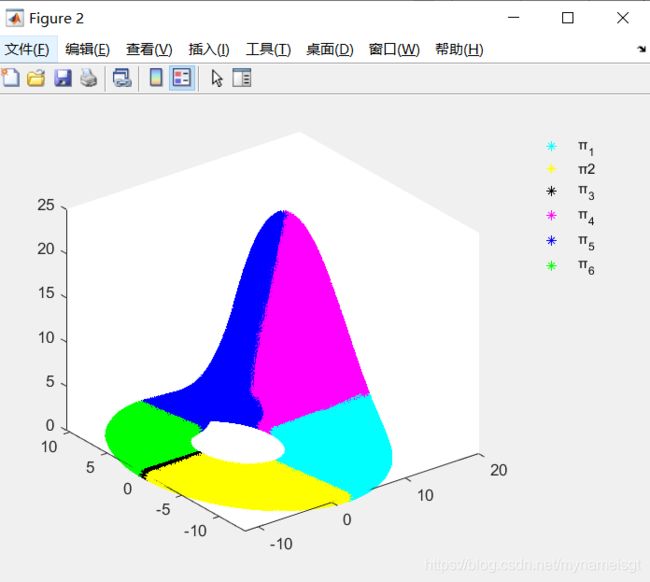
a=0.26时
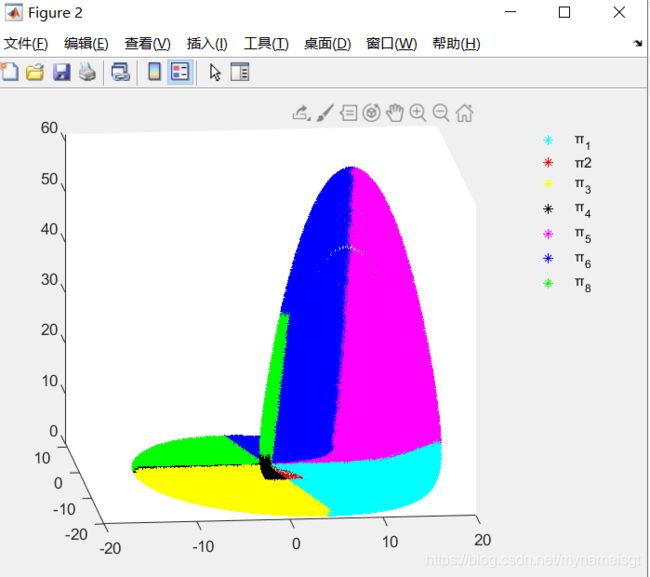
达到了文献的效果
根据表1中的顺序模式定义,Hénon映射的相空间分区被nullclines占用,如下所示:
这两条线如图 5(a) 所示,无论迭代步骤如何,我们都没有发现吸引子的点位于有序模式π4的区域中。 π4模式的消失表明,除了(0.63,0.19)的不稳定固定点(L1和L2的交点)之外,π4分区与吸引子之间没有交集。
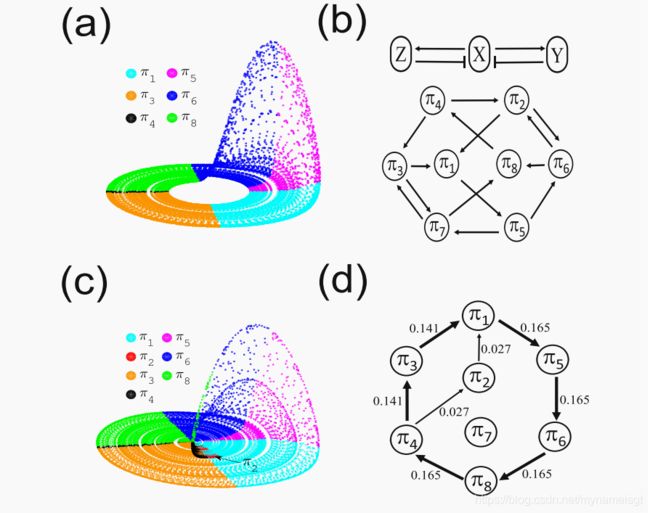
示例(2):Rössler系统,选择公式 4 作为连续动力系统。 当参数a = 0.165时,吸引子如图 6(a) 所示,相空间点由序号模式进一步进行颜色编码。 每个分区的边界由相应的零线确定,即dx / dt = 0,dy / dt = 0和dz / dt = 0。 顺序模式转换网络如图 4(d) 所示。 在这种情况下,π2和π7均不出现,解释如下 [47] 。 当将相空间转换为序数分区转换网络时,我们将每个状态(x,y,z)与诸如(+,-,+)之类的顺序模式相关联(如表 2 所示)。 此三维顺序模式描述了(x,y,z)的哪些变量在给定时间增加和减少。以变量x为例,由于雅可比行列式中的负号(-ω和-1),y和z都是x的抑制器。 但是,x是变量y的激活器,因为雅可比矩阵的元素在相空间中的每个地方都是ω为正。 Rössler系统的激活和抑制方案如图**6(b)**所示。
page eight
轨迹可以越过零线的条件意味着从增加到减少(反之亦然)相当于确定局部最大值或最小值。 由于系统的连续性,我们具有以下规则以具有最大值或最小值 [47] :(i)如果变量的所有阻遏物都减少而其所有激活物都增加,则变量不能具有最大值; (ii)如果变量的所有阻遏物都在增加而其所有的激活物都在减少,则变量不能具有最小值。 这两个规则产生了不同顺序模式之间的所有可能过渡,如图 6(b) 所示。 然而,在相空间中的典型轨迹观察到的过渡网络由给定的参数a和ω集合确定。 对于a = 0.165和ω= 1的情况,我们仅找到过渡路径π1→π5→π6→π8→π4→π3→π1(如图4(d) 所示),同时π2和π7是禁止的模式。 将a的值增加到0.26,Rössler系统呈现出具有不规则突跳的螺旋型混沌振荡,如图 6(c) 所示,产生了从π4→π2→π1的替代跃迁。 在此之前,我们观察到模式从π4到π1的两条过渡路径(图 6(d) ),而π7仍然不存在。 换句话说,π2图案的出现表明有序图案的变化对吸引子的几何变化敏感。
识别动态过渡。 我们使用序数分区过渡网络来识别两种不同情况下的动态过渡:(i)相干到非相干过渡,这是一个弱混沌-混沌过渡,(ii)到相同步过渡的路径。 在两个示例中,我们都显示了有序模式(无自环)的频率图,HO(有自环)和HT(无自环)的复杂度熵度量。此外,我们将情况(i)与相干性进行了比较 指数(CI)和情况(ii)表示每个振荡器的平均旋转频率Ωi。
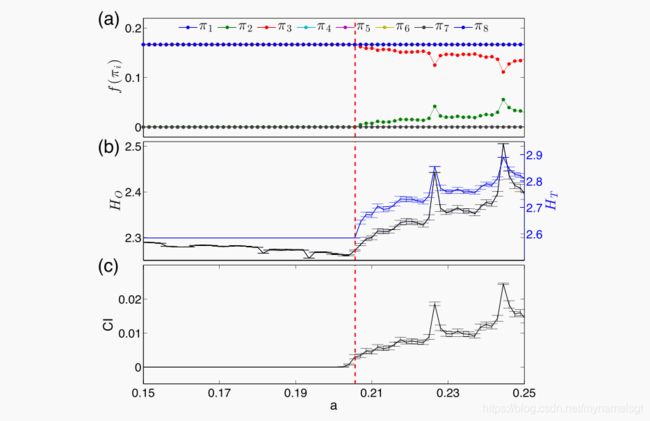
例(1)显示了混沌Rössler系统(公式**(4))中的相干到非相干转变,其中参数a在[0.15,0.25]范围内系统地变化。 正如参考文献中系统显示的那样。 如图48**所示,该参数范围包括不同的动力学,包括周期性窗口,相位相干混沌(在相空间中存在明确定义的旋转中心)以及非相位相干混沌振荡(缺少明显的旋转中心)。 相位相干和非相位相干混沌之间的过渡出现在ac≈0.206。 更具体地说,对于
图7显示了更改参数a时的分叉图。 首先,当a <ac时,有序模式π2的频率为零(f(π2)= 0),而当a> ac时,其频率为正。 相反,当a> ac时,f(π3)减小(图 7(a) )。 对于其他顺序模式π1,π4,π5,π6和π8,观察到的变化要小得多。 模式π7不会出现在a的整个间隔中。 顺序模式π2和π3对吸引子的几何变化敏感,捕获从相干相态到非相干态的过渡。
此外,当a
注意,HO,HT和相干指数的所有度量在周期性窗口中(例如,在a = 0.227和a = 0.245时)都显示出明显的局部最大值 48 。
例(2)显示了相位同步的路径,这由三个扩散耦合的Rössler系统通过x组件 49 演示。 方程阅读
其中k = 1、2、3和κ是耦合强度。 我们通过选择ω1= 0.98,ω2= 1.02,ω3= 1.06来考虑不同的振荡器。 参数a选择为0.165,以使子系统处于相干状态(图 6(a) )。 振荡器k = 2双向耦合到k = 1和k = 3,而在k = 1和k = 3之间没有直接耦合。 公式 (8) 通过四阶Runge Kutta方法进行数值积分,积分步骤h = 0.01。 丢弃前10000个瞬态数据点,并分析由150000个数据点组成的时间序列。 我们按照表 2 中所示的相同模式定义,从xk分量(即(x1,x2,x3))构造有序模式转换网络。
page nine
图7.Rössler系统的相干相干到非相干相干转变作为参数a的函数(误差线表示从系统的100个独立实现中为a的每个值获得的标准偏差:(a)每个序数模式的频率 f(πi),其中π1,π4,π5,π6和π8在a的整个范围内重叠。(b)熵值HO和HT,(c)相干指数(CI)。 垂直虚线突出显示了相干。
此处的关键是如何算CI(相干指数),通过了解公式(9)(10)(12)以及文献 [48],我对CI的求法有了一定认识。首先获取得到一串π模式的时间序列,对其进行扩充到复平面的操作(希尔伯特变换),matlab自带了hilbert函数,可帮助扩充到复平面.随后可得到φ(t),对φ(t)进行一阶差分,即Z=diff(φ),H(-)为heavisde函数,当括号内的数值大于0时记为1,否则记0.对Z使用heavisde函数后进行求均值即得到CI。
代码如下:
%初始数据,历时 452.128370 秒。
clear;clc
tic
global w %%定义全局变量w
global a; %%定义全局变量a
N=150000;h=0.01; %%迭代N次,步长h;
w=1.0;
iter=1;
for a=0.15:0.001:0.25 %对a,间隔0.001进行迭代
x=zeros(1,N);y=zeros(1,N);z=zeros(1,N); %%提前分配内存空间
x(1)=rand;y(1)=10*rand;z(1)=rand; %设定初始点
%四阶Runge-Kutta算法
for i=1:N
x_k1=f_dx(y(i),z(i));
y_k1=f_dy(x(i),y(i));
z_k1=f_dz(x(i),z(i));
x_k2=f_dx(y(i)+h/2*y_k1,z(i)+h/2*z_k1);
y_k2=f_dy(x(i)+h/2*x_k1,y(i)+h/2*y_k1);
z_k2=f_dz(x(i)+h/2*x_k1,z(i)+h/2*z_k1);
x_k3=f_dx(y(i)+h/2*y_k2,z(i)+h/2*z_k2);
y_k3=f_dy(x(i)+h/2*x_k2,y(i)+h/2*y_k2);
z_k3=f_dz(x(i)+h/2*x_k1,z(i)+h/2*z_k2);
x_k4=f_dx(y(i)+h*y_k3,z(i)+h*z_k3);
y_k4=f_dy(x(i)+h*x_k3,y(i)+h*y_k3);
z_k4=f_dz(x(i)+h*x_k3,z(i)+h*z_k3);
x(i+1)=x(i)+h/6*(x_k1+2*x_k2+2*x_k3+x_k4);
y(i+1)=y(i)+h/6*(y_k1+2*y_k2+2*y_k3+y_k4);
z(i+1)=z(i)+h/6*(z_k1+2*z_k2+2*z_k3+z_k4);
end
%丢弃前clear_N个数据点后进行差分
clear_N=10000;
x(1:clear_N)=[];y(1:clear_N)=[];z(1:clear_N)=[];
delta_x=diff(x);delta_y=diff(y);delta_z=diff(z);
m=length(delta_x);
%记录π序数
pai_xushu=cell(1,m); %%直观显示对应的π模式
digit_xushu=zeros(1,m); %%编程序简易,以1->π1,2->π2,…,n->πn
for i=1:m %%得到m个π序数
if delta_x(i)>=0 && delta_y(i)>=0 && delta_z(i)>=0
pai_xushu{
i}='π1';
digit_xushu(i)=1;
elseif delta_x(i)>=0 && delta_y(i)>=0 && delta_z(i)<0
pai_xushu{
i}='π2';
digit_xushu(i)=2;
elseif delta_x(i)>=0 && delta_y(i)<0 && delta_z(i)>=0
pai_xushu{
i}='π3';
digit_xushu(i)=3;
elseif delta_x(i)>=0 && delta_y(i)<0 && delta_z(i)<0
pai_xushu{
i}='π4';
digit_xushu(i)=4;
elseif delta_x(i)<0 && delta_y(i)>=0 && delta_z(i)>=0
pai_xushu{
i}='π5';
digit_xushu(i)=5;
elseif delta_x(i)<0 && delta_y(i)>=0 && delta_z(i)<0
pai_xushu{
i}='π6';
digit_xushu(i)=6;
elseif delta_x(i)<0 && delta_y(i)<0 && delta_z(i)>=0
pai_xushu{
i}='π7';
digit_xushu(i)=7;
else
pai_xushu{
i}='π8';
digit_xushu(i)=8;
end
end
%计算记录π模式概率p(πi)及其相应的熵值Ho
pai_count=zeros(1,8);
for i=1:m
for j=1:8
if digit_xushu(i) == j
pai_count(j)=pai_count(j)+1; %%记录对应πi出现的个数
end
end
end
P(:,iter)=pai_count/sum(pai_count); %%获得每个πi占总体的比例
P(find(P(:,iter)==0),iter)=1; %%消除概率为0取歧义对数的情况,log2(1)=0,不影响最后熵值结果
Ho(iter)=0;
for j=1:8
Ho(iter)=Ho(iter)-P(j,iter)*log2(P(j,iter));
end
P(find(P(:,iter)==1),iter)=0; %%复原
%计算π模式的转化概率以及HT
pai_ij_count=zeros(8,8);
for k=1:m-1
for i=1:8
for j=1:8
if digit_xushu(k) == i && digit_xushu(k+1) == j %%如果第k个π模式为πi,第k+1个π模式为πj
pai_ij_count(i,j)=pai_ij_count(i,j)+1; %%则在第i行第j列+1。最后可得到转移数量矩阵。
end
end
end
end
P_ij=pai_ij_count/sum(sum(pai_ij_count)); %%获得每个πi->πj的转移概率
P_ij(find(P_ij==0))=1; %%消除概率为0取歧义对数的情况,log2(1)=0,不影响最后熵值结果
HT(iter)=0;
for i=1:8
for j=1:8
HT(iter)=HT(iter)-P_ij(i,j)*log2(P_ij(i,j));
end
end
P_ij(find(P_ij==1))=0; %%复原
%去除自环后的概率及Ht
pai_ij_count_2=pai_ij_count-diag(diag(pai_ij_count)); %%对角线置0,去除自环现象
P_ij_2=pai_ij_count_2/sum(sum(pai_ij_count_2)); %%余下进行归一化得其转移概率
P_ij_2(find(P_ij_2==0))=1; %%消除概率为0取歧义对数的情况,log2(1)=0,不影响最后熵值结果
HT_2(iter)=0;
for i=1:8
for j=1:8
HT_2(iter)=HT_2(iter)-P_ij_2(i,j)*log2(P_ij_2(i,j));
end
end
P_ij_2(find(P_ij_2==1))=0; %%复原
%记录相干指数
XX=digit_xushu;
YY=hilbert(XX);
YY=imag(YY);
z=atan(XX./YY);
Dz=diff(z);
CI(iter)=sum(Dz<0)/length(Dz);
iter=iter+1;
end
%%绘图区
figure(1)
mm=0.15:0.001:0.25; %%画图所需对应x轴
subplot(3,1,1);
plot(mm,P(1,:),'b*-');hold on;
plot(mm,P(2,:),'g*-');hold on;
plot(mm,P(3,:),'r*-');hold on;
plot(mm,P(4,:),'c*-');hold on;
plot(mm,P(5,:),'m*-');hold on;
plot(mm,P(6,:),'y*-');hold on;
plot(mm,P(7,:),'k*-');hold on;
plot(mm,P(8,:),'w*-');hold off;
ylabel('f(π_i)');
% h1=legend('π_1','π_2','π_3','π_4','π_5','π_6','π_7','π_8');
% set(h1,'Orientation','horizon');
% set(h1,'Box','off');
subplot(3,1,2);
[AX,H1,H2]=plotyy(mm,Ho,mm,HT,'plot'); %%设置双坐标
HH1=get(AX(1),'Ylabel'); %%设置图例
set(HH1,'String','H_o'); %%设置图例
HH2=get(AX(2),'Ylabel');
set(HH2,'String','H_T');
subplot(3,1,3)
plot(mm,CI,'-');
ylabel('CI');
toc
%由公式4所得函数
function f=f_dx(y,z) %%dx/dt
global w
f=-w*y-z;
end
function f=f_dy(x,y) %%dy/dt
global w
global a
f=w*x+a*y;
end
function f=f_dz(x,z) %%dz/dt
f=0.4+z*(x-8.5);
end
结果如下:
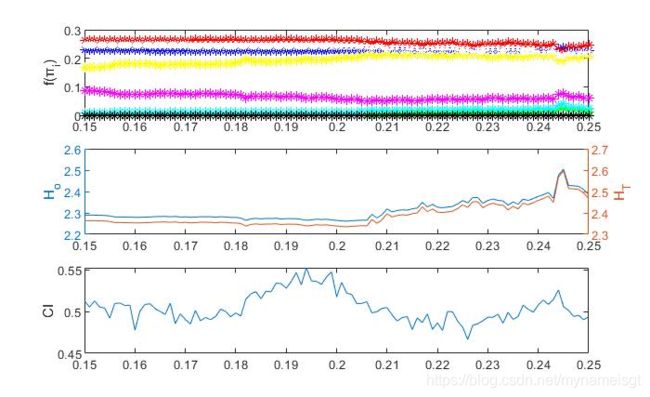
我们发现此图与文献中的图有些许差异,首先体现在f( π i π_i πi)上,我认为出现这类现象的原因或许是初始点的选取,导致π模式概率和文献有所差异,Ho和HT有和文献中同样的性质,在a=0.206从相干到非相干,a=0.226和a=0.245都出现了局部最大值。这里性质和文献符合。
我们使用公式 (8) 的动机是研究相位同步路径上序数模式的变化,重点是具有不同同步机制的过渡网络的演化过程,这比单个Rössler系统的情况更为复杂。 结果如图 8 所示。此外,当对等式进行积分时,图片 8 的结果已在50个随机初始条件下取平均值由公式 (8) 。
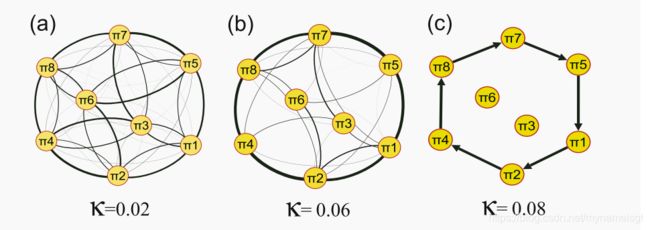
在不同步状态下(κ<κc1= 0.036),三个振荡器几乎独立地演化,因此所有序数模式的频率相同,均为0.125。 仅当κ接近κc1时,梯度变化很小(图 8(a) )。 熵值HT对这些逐渐变化更敏感,表现出明显的下降趋势,而HO似乎是一个常数(图 8(b) )。 每个振荡器的平均旋转频率Ωk(请参见方法)显示在(图 8(c) )中,这在这种耦合方式下没有同步性。
在振荡器k = 1和k = 2之间出现相位同步但在k = 3时不出现相位同步的情况下(κ∈[kc1,kc2] = [0.036,0.077]),我们观察到阶模π1,π2的单调增长趋势 ,π7和π8(图 8(a) )。 此外,我们发现π4和π5模式的增长趋势相对较慢。 相反,发现π3和π6有一些单调递减趋势。 熵值HO和HT都记录了阶次模式的频率变化,显示出逐渐减小的趋势(图 8(b) )。 平均旋转频率Ωk在图 8(c) 中显示,其中k = 1和k = 2锁相到相同的旋转频率,但k = 3则不。
在所有振荡器都处于相位同步状态(κ>κc2= 0.077)的状态下,我们发现模式π1,π2,π4,π5,π7,π8的频率收敛到相同的值f(πi)= 1/6,而π3 和π6不存在(图 8(a) )。 换句话说,如果所有振荡器都同步,则会观察到π3和π6的禁止模式。 熵HO显示出类似抛物线的趋势(先增大然后缓慢减小),但是HT为2.585的常数(图 8(b) )。 由于三个振荡器是锁相的,所以所有平均旋转频率都收敛到相同的值(图 8(c) )。
从耦合振荡器的高维系统的观点来看,在从非同步到相位同步的过程中,我们发现过渡网络经历了所有可能的有序模式之间的相当随机的过渡,变成了有限数量的有序模式之间的过渡状态。 如图9 所示。此外,如果所有三个振荡器都同步,我们发现π3和π6是禁止模式
page ten
图 8 .三个耦合的Rössler系统的相位同步转换。 (a)每个顺序模式的频率f(πi),(b)熵值HO和HT,(c)每个振荡器的平均旋转频率Ωi。 子系统k1和k2在κc1= 0.036处同步,而k3仅在更强的耦合强度κc2= 0.077时才加入同步。 两个临界耦合值都由垂直虚线突出显示。
图8讨论多路径情况下的振荡频率的关系,首先我们需要理解公式8的含义。其中有一句话:振荡器k = 2双向耦合到k = 1和k = 3,而在k = 1和k = 3之间没有直接耦合。对此,在我的理解中当k=1或3时, ∑ k k , l \sum k_{k,l} ∑kk,l只有一项这一项中的是 k 1 , 2 k_{1,2} k1,2或者 k 3 , 2 k_{3,2} k3,2对此,使用四阶Runge Kutta方法会复杂点。
提供代码如下:
%%公式(8)历时 1855.851394 秒。
%初始数据
clear;clc
tic
global w1
global w2
global w3
global a
global KL
N=150000;h=0.01; %迭代N次,步长h
w1=0.98;w2=1.02;w3=1.06;a=0.165; %振荡器w,参数a
iter=1;
for KL=0:0.001:0.1
%四阶Runge-Kutta算法
x1=zeros(1,N);y1=zeros(1,N);z1=zeros(1,N);
x2=zeros(1,N);y2=zeros(1,N);z2=zeros(1,N);
x3=zeros(1,N);y3=zeros(1,N);z3=zeros(1,N);
x1(1)=rand;y1(1)=10*rand;z1(1)=rand; %设定第一组初始点
x2(1)=rand;y2(1)=10*rand;z2(1)=rand; %设定第二组初始点
x3(1)=rand;y3(1)=10*rand;z3(1)=rand; %设定第三组初始点
for i=1:N
%算k1
x1_k1=f_dx1(x1(i),y1(i),z1(i),x2(i));
y1_k1=f_dy1(x1(i),y1(i));
z1_k1=f_dz(x1(i),z1(i));
x2_k1=f_dx2(x2(i),y2(i),z2(i),x1(i)+x3(i));
y2_k1=f_dy2(x2(i),y2(i));
z2_k1=f_dz(x2(i),z2(i));
x3_k1=f_dx3(x3(i),y3(i),z3(i),x2(i));
y3_k1=f_dy3(x3(i),y3(i));
z3_k1=f_dz(x3(i),z3(i));
%算k2
x1_k2=f_dx1(x1(i)+h/2*x1_k1,y1(i)+h/2*y1_k1,z1(i)+h/2*z1_k1,x2(i)+h/2*x2_k1);
y1_k2=f_dy1(x1(i)+h/2*x1_k1,y1(i)+h/2*y1_k1);
z1_k2=f_dz(x1(i)+h/2*x1_k1,z1(i)+h/2*z1_k1);
x2_k2=f_dx2(x2(i)+h/2*x2_k1,y2(i)+h/2*y2_k1,z2(i)+h/2*z2_k1,x1(i)+h/2*x1_k1+x3(i)+h/2*x3_k1);
y2_k2=f_dy2(x2(i)+h/2*x2_k1,y2(i)+h/2*y2_k1);
z2_k2=f_dz(x2(i)+h/2*x2_k1,z2(i)+h/2*z2_k1);
x3_k2=f_dx3(x3(i)+h/2*x3_k1,y1(i)+h/2*y3_k1,z3(i)+h/2*z3_k1,x2(i)+h/2*x2_k1);
y3_k2=f_dy3(x3(i)+h/2*x3_k1,y1(i)+h/2*y3_k1);
z3_k2=f_dz(x3(i)+h/2*x3_k1,z1(i)+h/2*z3_k1);
%算k3
x1_k3=f_dx1(x1(i)+h/2*x1_k2,y1(i)+h/2*y1_k2,z1(i)+h/2*z1_k2,x2(i)+h/2*x2_k2);
y1_k3=f_dy1(x1(i)+h/2*x1_k2,y1(i)+h/2*y1_k2);
z1_k3=f_dz(x1(i)+h/2*x1_k2,z1(i)+h/2*z1_k2);
x2_k3=f_dx2(x2(i)+h/2*x2_k2,y2(i)+h/2*y2_k2,z2(i)+h/2*z2_k2,x1(i)+h/2*x1_k2+x3(i)+h/2*x3_k2);
y2_k3=f_dy2(x2(i)+h/2*x2_k2,y2(i)+h/2*y2_k2);
z2_k3=f_dz(x2(i)+h/2*x2_k2,z2(i)+h/2*z2_k2);
x3_k3=f_dx3(x3(i)+h/2*x3_k2,y3(i)+h/2*y3_k2,z3(i)+h/2*z3_k2,x2(i)+h/2*x2_k2);
y3_k3=f_dy3(x3(i)+h/2*x3_k2,y3(i)+h/2*y3_k2);
z3_k3=f_dz(x3(i)+h/2*x3_k2,z3(i)+h/2*z3_k2);
%算k4
x1_k4=f_dx1(x1(i)+h*x1_k3,y1(i)+h*y1_k3,z1(i)+h*z1_k3,x2(i)+h/2*x2_k3);
y1_k4=f_dy1(x1(i)+h*x1_k3,y1(i)+h*y1_k3);
z1_k4=f_dz(x1(i)+h*x1_k3,z1(i)+h*z1_k3);
x2_k4=f_dx2(x2(i)+h*x2_k3,y2(i)+h*y2_k3,z2(i)+h*z2_k3,x1(i)+h*x1_k3+x3(i)+h*x3_k3);
y2_k4=f_dy2(x2(i)+h*x2_k3,y2(i)+h*y2_k3);
z2_k4=f_dz(x2(i)+h*x2_k3,z2(i)+h*z2_k3);
x3_k4=f_dx3(x3(i)+h*x3_k3,y3(i)+h*y3_k3,z3(i)+h*z3_k3,x2(i)+h*x2_k3);
y3_k4=f_dy3(x3(i)+h*x3_k3,y3(i)+h*y3_k3);
z3_k4=f_dz(x3(i)+h*x3_k3,z3(i)+h*z3_k3);
%计算下一时刻
x1(i+1)=x1(i)+h/6*(x1_k1+2*x1_k2+2*x1_k3+x1_k4);
y1(i+1)=y1(i)+h/6*(y1_k1+2*y1_k2+2*y1_k3+y1_k4);
z1(i+1)=z1(i)+h/6*(z1_k1+2*z1_k2+2*z1_k3+z1_k4);
x2(i+1)=x2(i)+h/6*(x2_k1+2*x2_k2+2*x2_k3+x2_k4);
y2(i+1)=y2(i)+h/6*(y2_k1+2*y2_k2+2*y2_k3+y2_k4);
z2(i+1)=z2(i)+h/6*(z2_k1+2*z2_k2+2*z2_k3+z2_k4);
x3(i+1)=x3(i)+h/6*(x3_k1+2*x3_k2+2*x3_k3+x3_k4);
y3(i+1)=y3(i)+h/6*(y3_k1+2*y3_k2+2*y3_k3+y3_k4);
z3(i+1)=z3(i)+h/6*(z3_k1+2*z3_k2+2*z3_k3+z3_k4);
end
%丢弃前clear_N个数据点
clear_N=10000;
x1(1:clear_N)=[];x2(1:clear_N)=[];x3(1:clear_N)=[];
y1(1:clear_N)=[];y2(1:clear_N)=[];y3(1:clear_N)=[];
z1(1:clear_N)=[];z2(1:clear_N)=[];z3(1:clear_N)=[];
%--------------------------------------------------------------------------
delta_x1=diff(x1);delta_x2=diff(x2);delta_x3=diff(x3); %%由题目要求,设定xk(k=1,2,3)的时间序列
m=length(delta_x1);
%记录π序数
pai_xushu=cell(1,m);
digit_xushu=zeros(1,m);
for i=1:m %%得到m个π序数
if delta_x1(i)>=0 && delta_x2(i)>=0 && delta_x3(i)>=0
pai_xushu{
i}='π1';
digit_xushu(i)=1;
elseif delta_x1(i)>=0 && delta_x2(i)>=0 && delta_x3(i)<0
pai_xushu{
i}='π2';
digit_xushu(i)=2;
elseif delta_x1(i)>=0 && delta_x2(i)<0 && delta_x3(i)>=0
pai_xushu{
i}='π3';
digit_xushu(i)=3;
elseif delta_x1(i)>=0 && delta_x2(i)<0 && delta_x3(i)<0
pai_xushu{
i}='π4';
digit_xushu(i)=4;
elseif delta_x1(i)<0 && delta_x2(i)>=0 && delta_x3(i)>=0
pai_xushu{
i}='π5';
digit_xushu(i)=5;
elseif delta_x1(i)<0 && delta_x2(i)>=0 && delta_x3(i)<0
pai_xushu{
i}='π6';
digit_xushu(i)=6;
elseif delta_x1(i)<0 && delta_x2(i)<0 && delta_x3(i)>=0
pai_xushu{
i}='π7';
digit_xushu(i)=7;
else
pai_xushu{
i}='π8';
digit_xushu(i)=8;
end
end
%--------------------------------------------------------------------------
delta_x1=diff(x1);delta_y1=diff(y1);delta_z1=diff(z1); %%x1,y1,z1序列,用来获取Ω1
m=length(delta_x1);
%记录π序数
digit_xushu1=zeros(1,m);
for i=1:m %%得到m个π序数
if delta_x1(i)>=0 && delta_y1(i)>=0 && delta_z1(i)>=0
digit_xushu1(i)=1;
elseif delta_x1(i)>=0 && delta_y1(i)>=0 && delta_z1(i)<0
digit_xushu1(i)=2;
elseif delta_x1(i)>=0 && delta_y1(i)<0 && delta_z1(i)>=0
digit_xushu1(i)=3;
elseif delta_x1(i)>=0 && delta_y1(i)<0 && delta_z1(i)<0
digit_xushu1(i)=4;
elseif delta_x1(i)<0 && delta_y1(i)>=0 && delta_z1(i)>=0
digit_xushu1(i)=5;
elseif delta_x1(i)<0 && delta_y1(i)>=0 && delta_z1(i)<0
digit_xushu1(i)=6;
elseif delta_x1(i)<0 && delta_y1(i)<0 && delta_z1(i)>=0
digit_xushu1(i)=7;
else
digit_xushu1(i)=8;
end
end
%-----------------------------------------------------------------------------------------------------
delta_x2=diff(x2);delta_y2=diff(y2);delta_z2=diff(z2); %%x2,y2,z2序列,用来获取Ω2
m=length(delta_x2);
%记录π序数
digit_xushu2=zeros(1,m);
for i=1:m %%得到m个π序数
if delta_x2(i)>=0 && delta_y2(i)>=0 && delta_z2(i)>=0
digit_xushu2(i)=1;
elseif delta_x2(i)>=0 && delta_y2(i)>=0 && delta_z2(i)<0
digit_xushu2(i)=2;
elseif delta_x2(i)>=0 && delta_y2(i)<0 && delta_z2(i)>=0
digit_xushu2(i)=3;
elseif delta_x2(i)>=0 && delta_y2(i)<0 && delta_z2(i)<0
digit_xushu2(i)=4;
elseif delta_x2(i)<0 && delta_y2(i)>=0 && delta_z2(i)>=0
digit_xushu2(i)=5;
elseif delta_x2(i)<0 && delta_y2(i)>=0 && delta_z2(i)<0
digit_xushu2(i)=6;
elseif delta_x2(i)<0 && delta_y2(i)<0 && delta_z2(i)>=0
digit_xushu2(i)=7;
else
digit_xushu2(i)=8;
end
end
%------------------------------------------------------------------------------------------------------
delta_x3=diff(x3);delta_y3=diff(y3);delta_z3=diff(z3); %%x3,y3,z3序列,用来获取Ω3
m=length(delta_x3);
%记录π序数
digit_xushu3=zeros(1,m);
for i=1:m %%得到m个π序数
if delta_x3(i)>=0 && delta_y3(i)>=0 && delta_z3(i)>=0
digit_xushu3(i)=1;
elseif delta_x2(i)>=0 && delta_y2(i)>=0 && delta_z2(i)<0
digit_xushu3(i)=2;
elseif delta_x3(i)>=0 && delta_y3(i)<0 && delta_z3(i)>=0
digit_xushu3(i)=3;
elseif delta_x3(i)>=0 && delta_y3(i)<0 && delta_z3(i)<0
digit_xushu3(i)=4;
elseif delta_x3(i)<0 && delta_y3(i)>=0 && delta_z3(i)>=0
digit_xushu3(i)=5;
elseif delta_x3(i)<0 && delta_y3(i)>=0 && delta_z3(i)<0
digit_xushu3(i)=6;
elseif delta_x3(i)<0 && delta_y3(i)<0 && delta_z3(i)>=0
digit_xushu3(i)=7;
else
digit_xushu3(i)=8;
end
end
%----------------------------------------------------------------------------------------------------
%计算记录π模式概率p(πi)及其相应的熵值Ho
pai_count=zeros(1,8);
for i=1:m
for j=1:8
if digit_xushu(i) == j
pai_count(j)=pai_count(j)+1; %%记录对应πi出现的个数
end
end
end
P(:,iter)=pai_count/sum(pai_count); %%获得每个πi占总体的比例
Ho(iter)=0;
for j=1:8
if P(j)~=0
Ho(iter)=Ho(iter)-P(j,iter)*log2(P(j,iter));
end
end
%计算π模式的转化概率以及HT
pai_ij_count=zeros(8,8);
for k=1:m-1
for i=1:8
for j=1:8
if digit_xushu(k) == i && digit_xushu(k+1) == j %%如果第k个π模式为πi,第k+1个π模式为πj
pai_ij_count(i,j)=pai_ij_count(i,j)+1; %%则在第i行第j列+1。最后可得到转移数量矩阵。
end
end
end
end
P_ij=pai_ij_count/sum(sum(pai_ij_count)); %%获得每个πi->πj的转移概率
HT(iter)=0;
for i=1:8
for j=1:8
if P_ij(i,j)~=0
HT(iter)=HT(iter)-P_ij(i,j)*log2(P_ij(i,j));
end
end
end
%去除自环后的概率及Ht
pai_ij_count_2=pai_ij_count-diag(diag(pai_ij_count)); %%对角线置0,去除自环现象
P_ij_2=pai_ij_count_2/sum(sum(pai_ij_count_2)); %%余下进行归一化得其转移概率
HT_2(iter)=0;
for i=1:8
for j=1:8
if P_ij_2(i,j)~=0
HT_2(iter)=HT_2(iter)-P_ij_2(i,j)*log2(P_ij_2(i,j));
end
end
end
%------------------以下是获得Ωi------------------------
%得Ω1
XX1=digit_xushu1;
YY1=hilbert(XX1);
YY1=imag(YY1);
z1=atan(XX1./YY1);
Dz1=diff(z1);
OM1(iter)=mean(Dz1)/(2*pi);
%得Ω2
XX2=digit_xushu2;
YY2=hilbert(XX2);
YY2=imag(YY2);
z2=atan(XX2./YY2);
Dz2=diff(z2);
OM2(iter)=mean(Dz2)/(2*pi);
%得Ω3
XX3=digit_xushu3;
YY3=hilbert(XX3);
YY3=imag(YY3);
z3=atan(XX3./YY3);
Dz3=diff(z3);
OM3(iter)=mean(Dz3)/(2*pi);
iter=iter+1;
end
%%绘图区
figure(1)
mm=0:0.001:0.1; %%画图所需对应x轴
subplot(3,1,1);
plot(mm,P(1,:),'b*-');hold on;
plot(mm,P(2,:),'g*-');hold on;
plot(mm,P(3,:),'r*-');hold on;
plot(mm,P(4,:),'c*-');hold on;
plot(mm,P(5,:),'m*-');hold on;
plot(mm,P(6,:),'y*-');hold on;
plot(mm,P(7,:),'k*-');hold on;
plot(mm,P(8,:),'w*-');hold off;
ylabel('f(π_i)');
% h1=legend('π_1','π_2','π_3','π_4','π_5','π_6','π_7','π_8');
% set(h1,'Orientation','horizon');
% set(h1,'Box','off');
subplot(3,1,2);
[AX,H1,H2]=plotyy(mm,Ho,mm,HT,'plot'); %%设置双坐标
HH1=get(AX(1),'Ylabel');
set(HH1,'String','H_o');
HH2=get(AX(2),'Ylabel');
set(HH2,'String','H_T');
subplot(3,1,3)
plot(mm,OM1,'r');hold on;
plot(mm,OM2,'b');hold on;
plot(mm,OM3,'g');hold on;
xlabel('k');ylabel('Ω_i');
toc
%由公式(8)所得函数
function f=f_dx1(x,y,z,xx) %%对dx1/dt,
global w1
global KL
f=-w1*y-z+KL*(xx-x);
end
function f=f_dx3(x,y,z,xx) %%dx3/dt
global w3
global KL
f=-w3*y-z+KL*(xx-x);
end
function f=f_dx2(x,y,z,xx) %%dx2/dt
global w2
global KL
f=-w2*y-z+KL*(xx-2*x);
end
function f=f_dy1(x,y) %%dy1/dt
global w1
global a
f=w1*x+a*y;
end
function f=f_dy2(x,y) %%dy2/dt
global w2
global a
f=w2*x+a*y;
end
function f=f_dy3(x,y) %%dy3/dt
global w3
global a
f=w3*x+a*y;
end
function f=f_dz(x,z) %%dz/dt
f=0.4+z*(x-8.5);
end
结果如下:
与原文献有较大的差异,或许是此处的代码编写有误。
结论
在这项工作中,我们提出了从多元时间序列构建有序分区转换网络,这有助于我们分析不同组件之间的交互模式。 基本思想是捕获相关速度空间中变化的方向,从而在原始相空间中产生动态信息,而不是静态信息。 所得的有序分区转换网络是加权有向网络,从根本上来说,它们与递归网络 [19] 和可见性图 [10] 不同。 对于来自离散和连续动力系统的时间序列,我们发现观察到的序数模式的频率是不均匀的,这由熵HO来量化。 另外,不同序数模式之间的过渡频率也是不均匀的,其特征在于熵HT。 请注意,对于离散系统,HO和HT之间不会有本质区别,但是对于连续系统,HT是表征有序分区转换网络的更好方法,因为HO受自环的影响更大,如图 [4] 所示。
顺序分区转换网络利用零折线生成分区,从而在相空间中生成时间序列的马尔可夫链表示。 两个序数模式之间的过渡取决于变量增量的符号变化。 正如我们在混沌Rössler系统中所证明的那样,此定义对于捕获相空间的几何变化非常敏感,例如从相干到非相干过渡。
请注意,我们的序数分区过渡网络生成算法与最近构建时空网络以捕获内存效应的工作不同 [50] 。 通过顺序分区转换网络来表征存储效应将是未来的课题。 另外,我们集中于每个变量的嵌入维Dx = 2和延迟τ= 1,它捕获了不同空间中时间序列的上升或下降趋势。 可以肯定地将算法推广到更高的Dx和τ值,但是,对计算的要求更高。 例如,在n维多元序列[{x1}(t),…,{xn}(t)]中,如果D. {x1} = … =,则有(3!)^ n个序数模式。 D. {xn} = 3。 另外,转移矩阵W的尺寸为(3!)^n× (3!)^n。 同时,尺寸Dx的增加需要更长的时间序列,以便更可靠地估计顺序图案的转变频率。 从算法的角度来看,通过使用较大的时间延迟τ> 1不会引入任何计算复杂性,但是,对于变量的速度缺乏适当的解释。 从短时间序列可靠地估计序数分区转换矩阵存在一个未解决的问题,尤其是在噪声起重要作用的情况下。
page eleven
图9.公式 (8) 的相位同步路径上的顺序转换网络,为三种典型的耦合强度。 (a)非同步状态下κ= 0.02 <κc1的随机跃迁,(b)主导结构出现在振荡器k = 1和k = 2是相位同步的状态下,但不与k = 3,κ= 0.06 ∈[κc1,κc2],(c)当所有三个振荡器都被锁相时,仅观察到一种序数模式的跃迁路径,κ= 0.08>κc2。
链接的粗细由过渡网络中的相关频率确定,并且消除了自环。 在(a,b)中,为便于可视化,链接箭头被抑制。
…
我们已经应用了序数分区过渡网络来研究相位同步的路径,表明当耦合强度随着不同的同步过渡机制而增加时,网络中会出现主导过渡路径。 随着同步程度的提高,耦合系统的动力学特性被锁定到同步歧管,从而在最终的顺序分区网络中产生主导过渡路径。 在出现同步之前,另一项艰巨的任务是区分间接耦合方向和直接耦合方向 [49、51] ,这在气候数据分析中非常常见,即从远处的多通道时间序列中提取网络交互模式 [52] 。 在我们考虑的三个耦合Rössler子系统的情况下(公式 (8) ),振荡器k = 2双向耦合到k = 1和k = 3,而在k = 1和k =3之间没有直接耦合。 可以引入有序递归图 [45] 来解决此问题。
传统上,基于时间序列的序数符号表示的置换熵的计算不包括遵循相空间轨迹的模式转换行为。 相反,有序分区过渡网络方法明确考虑了时间演化信息,因此为传统的符号分析提供了很多补充性见解,显示了进行实验时间序列分析的巨大潜力。
方法:相干指数
在这里,我们总结了参考文献中计算相位相干指数的主要步骤。[48] .我们在这项工作中的注意力仅限于标准分析信号方法。 在此,使用希尔伯特变换将标量信号x(t)扩展到复平面
P.V. 表示柯西积分的主值,产生相位
上面的定义对于相位相干动力学很简单。 在非相位相干动力学中,基于解析信号53的局部曲率特性,提出了另一种相位定义 [53] ,即
由于在基于Hilbert变换的标准定义中,相位变量φ(t)不一定会随时间单调增加,因此我们对这种单调性进行了量化,以便获得用于相位相干的简单启发式阶参数,我们将其称为相干 指数
φ(t)=dφ(t)/ dt。 此外,然后将混沌振荡器的瞬时频率定义为相位变量相对于时间的导数。 随时间平均该属性可得出平均频率

![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-D1g81NJU-1611895510083)(C:\Users\Admin\AppData\Roaming\Typora\typora-user-images\image-20210110145254332.png)]](http://img.e-com-net.com/image/info8/1bcad0d535354d01ad7146f859c154ed.jpg)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Lp6vRcwq-1611895510083)(C:\Users\Admin\AppData\Roaming\Typora\typora-user-images\image-20210110145447416.png)]](http://img.e-com-net.com/image/info8/6636eb879b844d63b8895b0bf6ec91db.jpg)

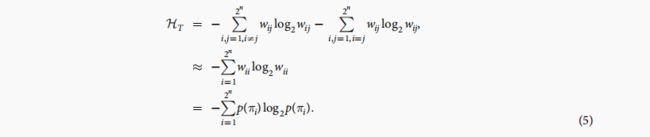
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TVZddflM-1611895510087)(C:\Users\Admin\AppData\Roaming\Typora\typora-user-images\image-20210110151006366.png)]](http://img.e-com-net.com/image/info8/9300395cc6e04bee9848b898ceaa3542.jpg)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6EchqpRp-1611895510088)(C:\Users\Admin\AppData\Roaming\Typora\typora-user-images\image-20210110151911251.png)]](http://img.e-com-net.com/image/info8/ebe4ad1d936849e5a7a9704aefb86f06.jpg)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-nXl5CsjJ-1611895510090)(C:\Users\Admin\AppData\Roaming\Typora\typora-user-images\image-20210110153836221.png)]](http://img.e-com-net.com/image/info8/00a0333faf524d5aa3fff5293434db7e.jpg)

![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-yh0Fs81b-1611895510097)(C:\Users\Admin\AppData\Roaming\Typora\typora-user-images\image-20210110164213051.png)]](http://img.e-com-net.com/image/info8/3bf048fca7f04672bd1be9c90370eeee.jpg)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-81yzzRha-1611895510098)(C:\Users\Admin\AppData\Roaming\Typora\typora-user-images\image-20210110164255400.png)]](http://img.e-com-net.com/image/info8/e1bf64d5037b44d188ed2430912d9946.jpg)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cFL41bJh-1611895510099)(C:\Users\Admin\AppData\Roaming\Typora\typora-user-images\image-20210110164355843.png)]](http://img.e-com-net.com/image/info8/f68e23f16406416cb04251a16cf86377.jpg)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5MGZpo57-1611895510100)(C:\Users\Admin\AppData\Roaming\Typora\typora-user-images\image-20210110164443647.png)]](http://img.e-com-net.com/image/info8/57115259699a4295a7d9967adbb93052.jpg)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-UwgcEhL2-1611895510101)(C:\Users\Admin\AppData\Roaming\Typora\typora-user-images\image-20210110164619471.png)]](http://img.e-com-net.com/image/info8/0a7cf58c390e49df888a3affbe4bd7a7.jpg)