数据结构与算法面试要点简明教程（七）—— 图

参考：https://blog.csdn.net/jiaoyangwm/article/details/80808235

https://blog.csdn.net/a2392008643/article/details/81781766

https://mp.weixin.qq.com/s/vn3KiV-ez79FmbZ36SX9lg

本文仅是将他人博客经个人理解转化为简明的知识点，供各位博友快速理解记忆，并非纯原创博客，如需了解详细知识点，请查看参考的各个原创博客。

目录

第七章  图

7.1  图的定义

7.2  图的存储结构

7.3  图的遍历

7.4  最短路径算法

7.5  最小生成树

7.6  拓扑排序

7.7  相关面试题

---

第七章  图

• 图是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G(V,E)，其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合。

7.1  图的定义

1、无向图

顶点之间没有方向，称这条边为无向边，全部由无向边构成图称为无向图（Undirected Graph）。

无向图

无向图中，如果任意两个顶点之间都存在边，则称该图为无向完全图，含有n个顶点的无向完全图有条边。

2、有向图

顶点之间有方向，称这条边为有向边，全部由有向边构成图称为无向图（Directed Graph）。

有向图

有向图中，如果任意两个顶点间都存在方向互为相反的两条弧，则称为有向完全图。含有n个顶点的有向完全图有n(n−1)条边。

3、连通图

无向图中，如果两个顶点之间有路径，说明两顶点是连通的，如果对于图中任意两个顶点都是连通的，则称该无向图是连通图。

图1非连通图，图2为连通图

4、连通分量

无向图中的极大连通子图称为连通分量。注意连通分量的概念，它强调：

• 要是连通的子图
• 连通子图含有极大顶点数
• 具有极大顶点数的连通子徒包含依附于顶点的所有边

如图1中，其连通分量包括图2和图3

有向图中，如果对于每一对vi,vj（vi不等于vj），从vi到vj都存在路径，称其为强连通图。

5、总结

7.2  图的存储结构

图的结构比较复杂，任意两个顶点之间都可能存在联系，所以不可能用简单的顺序存储结构来表示，所以用下面的五种方法来存储图。

7.2.1  邻接矩阵

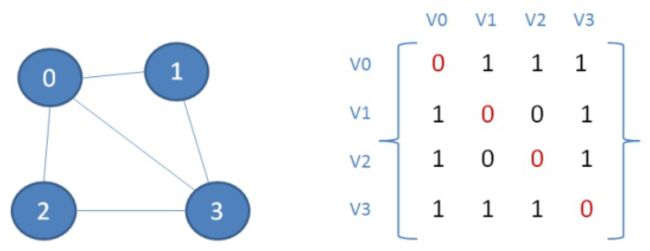
邻接矩阵用两个数组来表示图，一个一维数组存储图中顶点的信息，一个二维数组（称为邻接矩阵）存储图中的边或弧的信息。

如上图所示，顶点x和顶点y之间有边关联，那么矩阵中的元素A[x][y]与A[y][x]的值就是1，否则为0。像这样表达图中顶点关联关系的矩阵，就叫做邻接矩阵。

注意：

• 由于任何一个顶点与它自身是没有连接的，因此矩阵对角线，其上的元素值必然是0；
• 无向图对应的矩阵是一个对称矩阵。

邻接矩阵的优点就是简单直观，可以快速查到一个顶点和另一顶点之间的关联关系；缺点就是占用了太多空间。

7.2.2  邻接表和逆邻接表

为了解决邻接矩阵占用空间的问题，人们想到了另一种图的表示方法：邻接表。

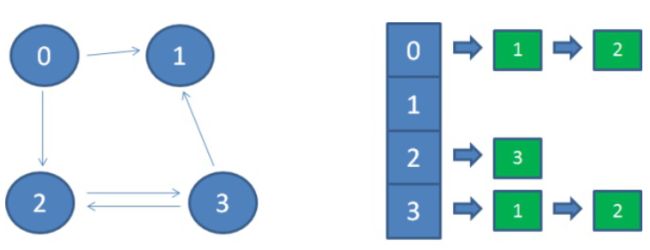
在邻接表中，图的每一个顶点都是一个链表的头结点，其后连接着该顶点能够直接达到的相邻顶点。

要想查出顶点x能够到达的所有相邻顶点，从顶点x向后的所有链表结点，就是顶点x能到达的相邻顶点；但是，如果要查找哪些点能到达顶点x，就只能去遍历每个顶点所在链表，看其链表中是否包含顶点x，这种逆向查找的方式略显麻烦，因此提出了逆邻接表的结构：

逆邻接表每一个顶点作为链表的头节点，后继节点所存储的是能够直接达到该顶点的相邻顶点。

因此，我们可以根据实际需求，选择使用邻接表还是逆邻接表。

7.2.3  十字链表

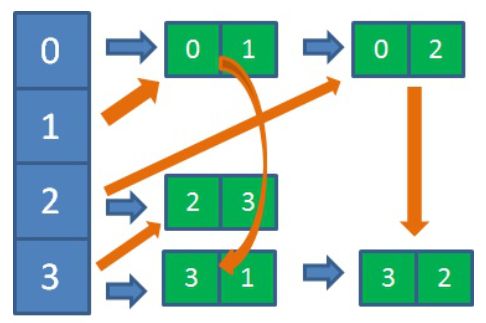
十字链表把邻接表和逆邻接表结合了起来，优化之后的十字链表，是下面这个样子：

图中蓝色为顶点，绿色为边，每一条带有蓝色箭头的链表，存储着从顶点出发的边；每一条带有橙色箭头的链表，存储着进入顶点的边。

7.2.4  邻接多重表

略

7.2.5  边集数组

略

7.3  图的遍历

从图中某一顶点出发访问图中其余顶点，且使每一个顶点仅被访问一次，该过程叫图的遍历。

7.3.1  深度优先遍历（Depth First Search, DFS）

深度优先遍历类似于树的前序遍历，其遍历整个图的方法是：

• 访问顶点v；
• 依次从v的未被访问的邻接点出发，对图进行深度优先遍历，直到图中所有和v有路径相通的顶点都被访问到；
• 若此时图中尚有顶点未被访问，则从一个未被访问的顶点出发，重新进行深度优先遍历，直到图中所有顶点均被访问过为止。

1、DFS的基本结构

在程序实现 DFS 时需要考虑以下问题：

• 栈：用栈来保存当前节点信息，保证当遍历的新节点返回时能够继续遍历当前节点。
• 标记：需要对已经遍历过的节点进行标记。

//非递归的DFS用栈来实现，递归式的DFS基本结构如下
void dfs(int[][] grid, int r, int c) {
    // 判断 base case，不满足条件立即返回
    if (!inArea(grid, r, c)) return;
    // 判断是否遍历过了
    if (grid[r][c] != 1) return;
    // 将格子标记为「已遍历过」
    grid[r][c] = 1; 
    // 访问邻接点
    dfs(grid, r - 1, c);
    dfs(grid, r + 1, c);
    dfs(grid, r, c - 1);
    dfs(grid, r, c + 1);
}

2、Backtracking

Backtracking（回溯）属于 DFS。

• 普通 DFS 主要用在 可达性问题 ，这种问题只需要执行到特点的位置然后返回即可。
• 而 Backtracking 主要用于求解 排列组合 问题。

因为 Backtracking 不是立即返回，而要继续求解，因此在程序实现时，需要注意对元素的标记问题：

• 在访问一个新元素进入新的递归调用时，需要将新元素标记为已经访问，这样才能在继续递归调用时不用重复访问该元素；
• 但是在递归返回时，需要将元素标记为未访问，因为只需要保证在一个递归链中不同时访问一个元素，可以访问已经访问过但是不在当前递归链中的元素。

string cur;
void backTracking(string digits){
    if(digits.size() == 0){
        res.push_back(cur);
    }else{
        char num = digits[0];
        string letter = mp[num];
        for(int i = 0; i < letter.size(); i++){
            cur.push_back(letter[i]);
            backTracking(digits.substr(1));
            cur.pop_back();
        }
    }
    return;
}

7.3.2  广度优先遍历（Breadth First Search, BFS）

广度优先遍历类似于树的层序遍历，先将某一结点入队，出队时将所有与其相连的结点入队，以此类推。

在程序实现 BFS 时需要考虑以下问题：

• 队列：用来存储每一轮遍历得到的节点；
• 标记：对于遍历过的节点，应该将它标记，防止重复遍历。

class Solution {
public:
    int shortestPathBinaryMatrix(vector>& grid) {
        int ans = 0;
        queue myQ; // BFS一般通过队列方式解决
        int M = grid.size();
        int N = grid[0].size();
        // 先判断边界条件，很明显，这两种情况下都是不能到达终点的。
        if (grid[0][0] == 1 || grid[M - 1][N - 1] == 1) return -1;
        // 备忘录，记录已经走过的结点
        vector> mem(M, vector(N, 0));
        //塞入初始结点
        myQ.push({0, 0});
        mem[0][0] = 1;
        // 以下是标准BFS的写法
        while (!myQ.empty()) {
            int size = myQ.size();
            for (int i = 0; i < size; i++) {
                Node currentNode = myQ.front();
                int x = currentNode.x;
                int y = currentNode.y;
                // 判断是否满足退出的条件
                if (x == (N - 1) && y == (M - 1)) return (ans + 1);
                // 下一个节点所有可能情况
                vector nextNodes = {
    {x + 1, y}, {x - 1, y}, {x + 1, y - 1}, {x + 1, y + 1},
                                          {x, y + 1}, {x, y - 1}, {x - 1, y - 1}, {x - 1, y + 1}};
                for (auto& n : nextNodes) {
                    // 过滤条件1： 边界检查
                    if (n.x < 0 || n.x >= N || n.y < 0 || n.y >= M) continue;
                    // 过滤条件2：备忘录检查
                    if (mem[n.y][n.x] == 1) continue;
                    // 过滤条件3：题目中的要求
                    if (grid[n.y][n.x] == 1) continue;
                    // 通过过滤筛选，加入队列！
                    mem[n.y][n.x] = 1;
                    myQ.push(n);
                }               
                myQ.pop();
            }
            ans++;
        }
        return -1;        
    }
};

7.3.3  总结

深度优先搜索用栈（stack）来实现，整个过程可以想象成一个倒立的树形：

1. 把根节点压入栈中。
2. 每次从栈中弹出一个元素，搜索所有在它下一级的元素，把这些元素压入栈中。并把这个元素记为它下一级元素的前驱。
3. 找到所要找的元素时结束程序，如果遍历整个树还没有找到，结束程序。

广度优先搜索使用队列（queue）来实现，整个过程也可以看做一个倒立的树形：

1. 把根节点放到队列的末尾。
2. 每次从队列的头部取出一个元素，查看这个元素所有的下一级元素，把它们放到队列的末尾。并把这个元素记为它下一级元素的前驱。
3. 找到所要找的元素时结束程序，如果遍历整个树还没有找到，结束程序。

几句话总结：

• 深度和广度优先遍历在时间复杂度上是一致的，若有N个结点、E条边，则遍历这个图的时间复杂度：邻接矩阵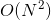、邻接表；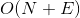
• 在空间复杂度上，DFS是有优势的，DFS不需要保存搜索过程中的状态，而BFS在搜索过程中需要保存搜索过的状态，而且一般情况需要一个队列来记录。
• 深度优先更适合以找到目标为主的情况（一般就是搜索全部解），广度优先更适合在不断扩大遍历访问时找到最优解的情况（一般就是求最短路径、最少次数等最优解）。

7.4  最短路径算法

最短路径是两顶点之间经过的边上权值之和最少的路径，并且成第一个顶点是源点，最后一个顶点是终点。

7.4.1  无权图的单源最短路径算法

在BFS的基础上做改动，首先定义dist[W]为S到W最短距离，path[W]为S到W路上经过的某顶点，初始化dist[S]=0，dist[W]=-1。

算法流程：

1. 源点S入队；
2. 进入while循环，若队列不为空，则从队列中弹出一个结点V；
3. 遍历结点V的邻接点W，若邻接点W没被访问过（dist[W]=-1），则dist[W] = dist[V]+1，且path[W]=V；
4. 再将该邻接点压入队列，不断循环直至遍历完整个图。

7.4.2  Dijkstra算法

迪杰斯特拉算法是一种有权图的单源最短路径算法。

主要思想：设有两个顶点集合S和T，S中存放已找到最短路径的顶点，T存放剩余顶点。初始时S只包含源点  ，然后不断从T中选取到  路径长度最短的顶点  并入集合S。集合S每并入一个新顶点，都要修改源点  到集合T中其他顶点的最短路径长度。不断重复此过程，直到T中顶点都并入S为止。

为了实现这一算法，应初始化三个数组：

•   表示  到 的最短路径长度（初态为与源点相邻的设为权值，其余为无穷）

•  表示  到 的最短路径中，的前一个顶点（初态为与源点相邻设为0，否则为-1）

•  表示  是否并入集合S了，并入为1，未并入为0

则迪杰斯特拉算法的伪代码描述如下：

void Dijkstra( Vertex s ){
	while(1){
	    V=未收录的顶点中dist最小者;
		if(找不到这样的V) break;
		collected[V] = true;
		for(V的每个邻接点W){
			if(collected[W] = false){
				if(dist[V]+E < dist[W]){
					dist[W] = dist[V]+E;
					path[W] = V;
				}
			}
		}
	}
}

注意：该算法不可解决负边的问题，时间复杂度为或者，路径的打印用堆栈。

7.4.3  Floyd算法

弗洛伊德算法是一种多源最短路径算法。

主要思想：设置两个矩阵A和Path，初始时将邻接矩阵直赋值给A，Path中元素全赋为-1。以顶点k为中间顶点，，对图中所有顶点对 {i, j} 进行检测，若  则将  的值修改为  的值， 改为k，否则什么都不做。

则弗洛伊德算法的伪代码如下：

void Floyd(){
    //矩阵A和Path的初始化
    for(i=0;iA[i][k]+A[k][j]){
                    A[i][j]=A[i][k]+A[k][j];
                    Path[i][j]=k;
                }
            }
        }
    }
}

注意：路径的打印用递归。

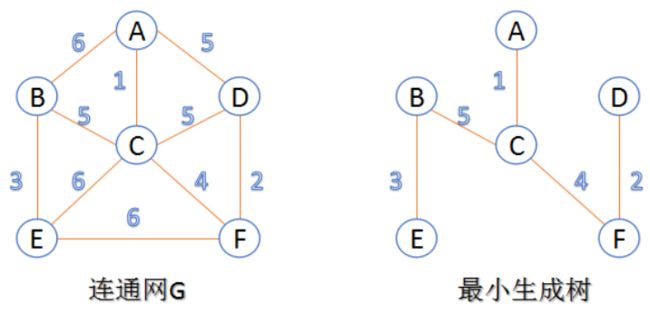
7.5  最小生成树

生成树：一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一棵有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。

最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。 

7.5.1  Kruskal算法

此算法可以称为“加边法”，初始最小生成树边数为0，每迭代一次就选择一条满足条件的最小代价边，加入到最小生成树的边集合里。 

1. 把图中的所有边按代价从小到大排序； 
2. 把图中的n个顶点看成独立的n棵树组成的森林； 
3. 按权值从小到大选择边，所选的边连接的两个顶点  应属于两颗不同的树，则这条边成为最小生成树的一条边，并将这两棵树合并成为一棵树；
4. 重复上述步骤，直到所有顶点都在一颗树内或者有n-1条边为止。

7.5.2  Prim算法

此算法可以称为“加点法”，每次迭代选择相对于树来说代价最小的边对应的点，加入到最小生成树中。算法从某一个顶点s开始，逐渐扩大覆盖整个连通网的所有顶点。

1. 图的所有顶点集合为V，初始时令集合u={s}，v=V−u;
2. 在两个集合 u,v 能够组成的边中，选择一条代价最小的边  ，加入到最小生成树中，并把  并入到集合 u 中。
3. 重复上述步骤，直到最小生成树有n-1条边或者n个顶点为止。

由于不断向集合u中加点，所以最小代价边必须同步更新；需要建立一个辅助数组closedge,用来维护集合v中每个顶点与集合u中最小代价边信息：

struct {
  char vertexData   //表示v中顶点
  unsigned int lowestCost   //该顶点到u的最小代价
} closEdge[vexCounts]

7.6  拓扑排序

拓扑序列：如果图中从V到W有一条有向路径，则V一定排在W之前，满足此条件的顶点序列成为一个拓扑序列。

获得一个拓扑序列的过程就称为拓扑排序。拓扑排序广泛应用在AOV（Activity on Vertex）网络和DAG（Directed Acyclic Graph）有向无环图中。个人理解：当要完成一件事时，拓扑排序就是给出完成事件的顺序，比如要先完成任务一，才能去完成任务二，以此类推。

简单来说，拓扑排序过程其实就是每次从图中找到入度为0的顶点打印出来，伪代码如下：

void TopoSort(){
	for(图中每个顶点V){
		if(Indegree(V) == 0) Enqueue(V,Q);
	}		
	while(!isEmpty(Q)){
		V=Dequeue(Q);
		输出V;
		count++;
		for(V的每个邻接点W){
			if(--Indegree(W)==0) Enqueue(W,Q);
		}
	}		
	if(count != |V|) Error("图中有回路");
}

下面给出一个例子：

 

7.7  相关面试题

Q：

A：