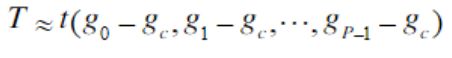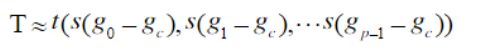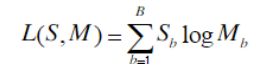图像处理——基于纹理分类的LBP算法及matlab+python算法实现
纹理是图像分析中的常用概念,是由于物体表面物理属性不同所引起的能够表示某个特定表面特征的灰度或者颜色信息。与其他图像特征相比,纹理反映了图像灰度模式的空间分布,包含了凸显更多表面信息及其周围环境的关系,更好的兼顾了图像的宏观信息与微观结构。但是在现实世界中的纹理并不像实验中的那么规整,存在着很多变化,而且,很多纹理分类的方法计算复杂度过高,难以实用化。为了解决这些问题,可以采用改进型的局部二值模式进行纹理分类。改进型的局部二值模式(Local Binary Patterns)具有灰度不变性、旋转不变性、.能够多分辨率分析等优点。
1 概述
二维纹理分析有许多潜在的应用,比如工业表面检查、遥感、生物图片分析,但是很少的例子能够成功发现纹理。主要的问题是现实世界中,由于方向、尺度及其他视觉外观的变化导致纹理常常是不均一的,灰度尺度不变性通常变得非常重要,因为不均匀的光照或图像内大幅变化变化。然而已经提出的纹理测量算法计算量太大,比如灰度共生矩阵等算法。
绝大多数纹理分类方法都显示或隐式的假设,待分类的位置样本与训练样本在空间大小、方向和灰度尺度属性上都一致。现实中的纹理受变化的光照条件影响,可以存在任意空间分辨率和旋转方向。
1.1 纹理
纹理是图像分析中常用的概念,是由于物体表面物理属性不同所引起的能够表示某个特定表面特征的灰度或者颜色信息。纹理是有许多相互接近的、互相编制的元素构成。在直观上反映为:图像的亮度、颜色的变化。
特点:与其他图像特征相比,纹理反映了图像灰度模式的空间分布,包含了凸显更多表面信息及其周围环境的关系,更好的兼顾了图像的宏观信息与微观结构。
1.2二维纹理
二维的纹理分析,具有很多潜在的应用。例如,工业表层检查,远程监控,生物制药图像分析等等领域。但是在实际应用时,会存在很多问题。主要的问题在于现实世界中的纹理并不像实验中的那么规整,存在着很多变化,
例如:1. 由于非均匀光源导致的光照变化;
2.实际的情况下,物体方向是随机的;
3.空间尺度不一致。
而且,很多纹理分类的方法计算复杂度过高,难以实用化。为了解决这些问题,可以采用改进型的局部二值模式进行纹理分类。改进型的局部二值模式(Local Binary Patterns)具有以下优点:
1.具有灰度不变性;
2.具有旋转不变性;
3.能够多分辨率分析;
2 LBP算法
2.1 LBP局部二值模式
LBP (Local Binary Pattern)——由T. Ojala、 M.Pietikäinen和 D. Harwood 在1994年提出,是一种用来描述图像局部纹理特征的算子[1][2]。 原始的LBP算子定义为在3*3的窗口内,以窗口中心像素为阈值,将相邻的8个像素的灰度值与其进行比较,若周围像素值大于中心像素值,则该像素点的位置被标记为1,否则为0。这样,3*3领域内的8个点可产生8bit的无符号数,即得到该窗口的LBP值,并用这个值来反映该区域的纹理信息。
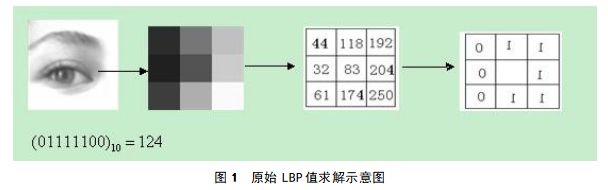
以图1为例介绍原始LBP值求解过程:
首先选择像素点83为中心点,选择中心点周围的8个作为邻居结点,邻居结点的像素值低于83的标记为0,比83高的标记为1,用0或1标记原始像素值,则中心点的像素值被LBP值所取代,假设以左上角的像素点作为起始点,顺时针标记得到LBP值的二进制表示为:(01111100)2对应十进制为124,即中心点像素值为83的对应的LBP值为124,以此类推求出整个图像所有点的LBP值,将LBP值代替原始像素值,得到这幅图像的LBP特征,并输出转化后的LBP纹理图像。
2.2 直方图统计
提取图像特征的目标无非就是为了进行分类,我们把一幅灰度图像转化为了LBP特征图像,从理论上讲并没有实现降维,也无法进行分类。这时引入直方图统计,,也就是统计LBP特征0~255各占的比例,进行数据的降维。将向量输入分类器中进行分类。由于只有256维特征,分类的效果并不好。
于是引入了图像分块处理的方法,如在人脸识别中,把脸分为7*7,5*5的区域,并对这49,25个小区域进行LBP处理,将每个小区域的直方图进行串联,就可以得到整个图像的LBP直方图。并对这个直方图进行分类处理,这样可以大大的增强分类的效果。但是分类数据维度也大大增加了,如果是7*7区域,数据维度为7*7*256=12544维。可以看出数据的维度还是比较大,所以需要进一步进行降维,这里就涉及了另外一个概念:Uniform LBP,即等价模式LBP,将在第四部分介绍。
3 具有灰度不变性和旋转不变性的LBP算法
3.1 灰度不变性
基本的LBP算子最大的缺陷在于它只覆盖了一个固定半径范围内的小区域,不能满足不同尺寸和频率纹理的需要。
未来适应不同尺度的纹理特征并达到灰度和旋转不变性的要求,2002年Ojala等人在PAMI上又发表了一篇关于LBP的文章,该文章非常详细清楚的阐述了多分辨率、灰度尺度不变和旋转不变、等价模式的改进的LBP特征[3][4]。对LBP算子进行了发展和改进,将3*3领域扩展到任意邻域,并用圆形邻域代替了正方形邻域,改进后的LBP算子允许在半径为R的圆形邻域内有任意多个像素点。
改进的LBP值求解示意图如图2所示:这里所给的是半径R=1(pixel)像素,像素点个数P=8时的情况。可以发现,R的大小决定了圆的大小,反映了二维空间的尺度;而P的大小决定了采样点数,反映了角度空间的分辨率。LBP值的求解与图1的求解过程类似,这里不再赘述。
3.1.1 灰度不变性算法
为了方便介绍LBP算子,首先做一些基本的定义。一个局部区域的 纹理分布可假设为局部区域内像素灰度的联合分布密度,定义如下:
其中P: 是指p个像素点
gc:局部邻域中心像素点的灰度值
gi:为半径R的圆形邻域内对距分布的P个点的空间像素点集的灰度值(i取0到p-1)
由于采样点在圆上,所以不一定会准确的落在像素点中,因此可能需要对采样点的位置进行插值获取采样点的像素估计值。
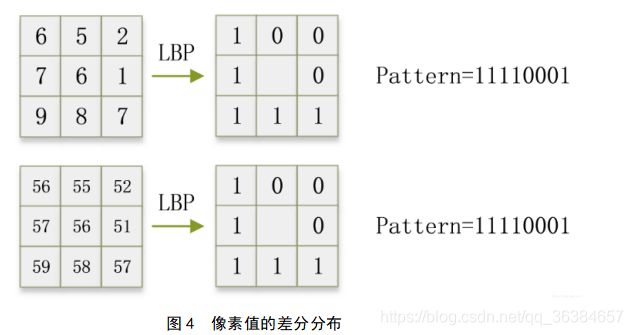
如下图所示,第一幅图像经过LBP变换后得到LBP值为11110001。而第二幅图像的每个像素在第一幅图像的基础上都增加了50,进行LBP变换后,得到的LBP值仍然是11110001。因为LBP特征反应了局部亮度的相对变化,所以整体增加或减少一个值对LBP特征并没有大的影响,因此得到结论:差分分布对平均光强不敏感。
因此,再不损失任何信息的前提下,如果将中心点gc的值从邻域像素的灰度值gp中减去则局部区域的纹理特征可以用中心点与周边像素之差的联合分布来表示:
然后假设查分gp-gc独立于gc,则上式改写为:
事实上,严格的独立式无法达成的,因此3-3式只是3-1式的一个近似值因式(t(gc)描述了图像的全局亮度(overall luminance),而非局部图像,不能为纹理分析提供有用的信息,因而上式可改写如下:
这是一个具有高度判别性的纹理算子,它在P维直方图中,记录了每个像素点邻域中纹理分布情况。在相对平滑以及灰度变化缓慢的区域,这些差值较小或接近于0,对于单个点,每个方向的的差值都比较大,在边缘处,某些方向的值比较大,而其他方向的值比较小。带符号的gp-gc不受平均亮度的影响,因而具有灰度不变性,我们仅使用差分的符号而不是差分本身的值来实现灰度尺度不变性。
其中s(x)为符号函数,当x不小于0时s取值为1,当x小于0时取值为0。3-5式得到的差分分布即为前面所说的LBP值的0、1分布。
3.2 旋转不变性
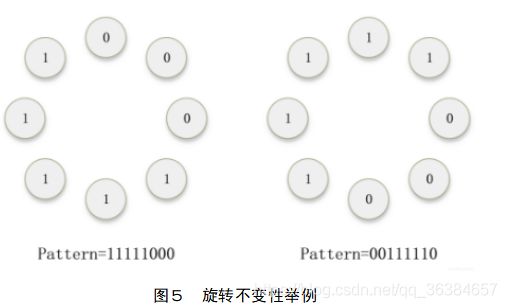
对于下图的两个模式,其实只有方向不同,在实际中是同一个模式的不同状态。为了克服旋转带来的变化,引入了“旋转不变性”方法。
处理方法如下:两种模式各有一个LBP值,将这个LBP值不断的循环右移并找到一个右移过程中最小的结果,作为新的LBP值。可见,这两种模式得到的新LBP值相同,属于同一张模式,从此解决了方向变化的问题。其中,“循环右移”的实质是对模式图案不断的旋转。“最小化”过程的实质是寻找能量最低的位置。以下是基于旋转不变性的LBP算法:
其中,ROR(x,i)执行沿时钟方向将P位数 X 移动 i 次。对于图像像素而言,就是将邻域集合按照时钟方向旋转很多次,直到当前旋转下构成的LBP值最小。
3.3 基于Uniform的灰度不变以及旋转不变LBP
加入了旋转不变性的LBP已经对原始的种类进行了优化,但T.Ojala发现效果并不是很好,因为当取P和R值很大时,也就意味着得到的局部二值模式的二进制的位数会非常大(P和R取值都很大,邻域内的像素就越多),这样最后产生的直方图就非常稀疏,不利于分类。相反,如果P和R取值都太小会使角度的分割精度降低,从而使得后面的分类性能降低。为解决这个问题,T.Ojala等人提出了“等价模式(uniform)”的方法降低LBP特征的维数[4]。
对于P=8的LBP,一共有8个采样点,每个采样点可能输出0或1,所以一共有256种局部二值模式。但其中有一些仅仅是方向不同,通过旋转之后可以重合。通过以上旋转不变性处理之后,256种LBP变为了具有“旋转不变性”的36种模式,如图6所示,这里黑色代表0,白色代表1。
在实际应用中,我们经过统计会发现, 图6中第一行的9种模式最为常见,而后面的27种模式并不常见。如果将后面的27种模式每种单独分类,会因为它们出现概率太小,而具有一定的随机性,因此分类结果反而不稳定。因此,我们要对这种方法进行改进。
这里引入基于uniform的旋转不变的LBP方式[5][6]:当某个局部二进制模式所对应的循环二进制数从O到1或从1到0最多有两次跳变时,该局部二进制模式所对应的二进制就称为一个等价模式uniform类。我们对每个LBP上的数值按顺序读一圈,将0->1和1->0变化的总次数记为U。对于上图可以发现,第一行模式的U值均小于等于2(反映了平坦或边缘区域),后面27种模式的U值均大于等于4(变化剧烈,不常见),如图7所示:
这样,对于一般LBP进行处理时,我们将U值小于等于2的LBP每个单独分为一类,而对于U值大于等于4的LBP全部归为一类,这样一共有P+2类。
得到基于Uniform的旋转不变以及灰度不变的LBP算法,见7式:
3.4直方图分布以及非参数化分类原理
3.4.1直方图分布
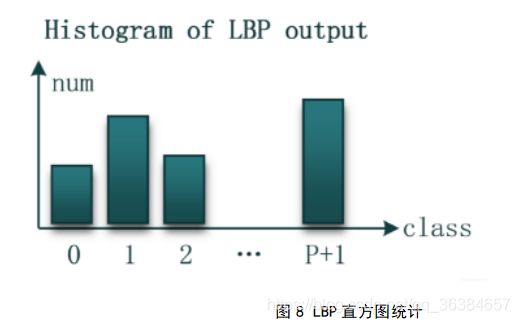
在LBP的应用中,如纹理分类、人脸分析等,一般都不将LBP图谱作为特征向量用于分类识别,而是采用LBP特征谱的统计直方图作为特征向量用于分类识别[7][8][9][10]。对于一幅图像,每个像素点均可以根据上述方法计算出一个LBP值,从而将这个像素归为(P+2)类中的一类。这样我们可以得到一个特征图,图中每点的数值代表像素点的类别,范围为:0~(P+1)。最终的纹理特征即为:LBP类别特征图的输出直方图。
3.4.2非参数化分类原理
常用非参数统计[12][13][14]的方法比较两个样本间LBP直方图分布的相似性,采用这种方法的优点在于可以避免对特征分布做假设。如果样本图像记为S,待匹配的模型M,Sb和Mb分别表示两个样本的LBP直方图中第b个Bin的概率分布,B表示直方图的总bin数,其中B=P+2。则样本S和模型M的匹配程度,使用最大对数似然(log-likelihood)统计方法表示:
距离L反映了样本S和M间的相似度,进行分类时,最简单的方式是将未知样本S归为距离L最小的类。一般采用的方式是计算待测样本S与所有训练样本M的距离,并将所有距离进行排序,然后将S归为距离最小的那一类。
3.4.3多分辨率分析
多分辨率分析[15][16]的基础是改变不同的R值和P值,实现不同的二维尺度分辨率和不同的角度空间分辨率。多分辨率分析,及改变不同的R值和P值,重复以上操作,最终将总的最大似然统计作为分类准则。如下公式所见,一共完成了N种不同的分辨率测度,最终的似然函数为:
4 实验
4.1 LBP算法实现
利用LBP算法对图像进行LBP特征值转化,即将原始像素点均用LBP值代替,得到输出的结果。
实验环境:MATlAB +win10操作系统
实验原始图像如图9(a)所示,读入图片,用LBP方法计算图像的LBP值:
- 选择第一个像素点,将其邻居像素值与所选中心点进行大小比较,小于中心点的值为0,大于中心点的值为1,则得到该中心点的LBP值。
- 遍历像素点矩阵,计算所有像素点的LBP值。
- 输出LBP特征值的图像。
matlab代码实现
实验准备
将lbp.m程序与lena.jpg图片放在一个文件位置,打开matlab运行lbp程序。
close all;
clc;
img=imread('lena.jpg');%读入图片
[m ,n]=size(img);%size求一个图像的规模,返回的是一个数组,标记为各维度的长度
imgn=zeros(m,n);%返回m*n数组
for i=2:m-1
for j=2:n-2
pow=0;
for p=i-1:i+1
for q =j-1:j+1
if img(p,q) > img(i,j)
if p~=i || q~=j
imgn(i,j)=imgn(i,j)+2^pow;
pow=pow+1;
end
end
end
end
end
end
figure;
imshow(imgn,[]);%输出图片
hist=cell(1,4); %cell(1,4)返回1*3元胞数组,划分四个区域求直方图
hist{1}=imhist(img(1:floor(m/2),1:floor(n/2)));%floor(m/2)朝负方向四舍五入m/2
hist{2}=imhist(img(1:floor(m/2),floor(n/2)+1:n));
hist{3}=imhist(img(floor(m/2)+1:m,1:floor(n/2)));
hist{4}=imhist(img(floor(m/2)+1:m,floor(n/2)+1:n));
for i=1:4
figure;
plot(hist{i});%画出四个直方图
end 实验原始图像如图9(a)所示,进行LBP转化后的结果如图9(b)所示。
将进行LBP计算后的图像按像素点的比例等比例的分为上下左右(对应a、b、c、d)四个部分,由于是原始的LBP方法计算的结果,因此分类的类别最大为255种类别,每种类别对应一个LBP值。直方图统计结果如图10所示:
从实验结果来看,传统的LBP算法可以大致的描绘出图像的轮廓,但分类的种别多,无法实现数据的降维,分类难度大,因此应该以改进的基于旋转不变和灰度不变LBP算法进行图像的纹理分类。
4.2 LBP进行纹理分类
采用改进的LBP方法提取图像的纹理信息,然后转化成直方图作为图像的特征,然后使用多分类的方法进行分类.
数据集:实验采用了40张不同风格的纹理图片,大小均为512*512像素,将每张图片分为大小相同的9块,其中5块作为训练集,剩余的4块作为测试集。
实验环境:python3.7+annconda+ jupyter notebook
实验方法:使用前文所述的LBP方法提取图像的纹理特征,对纹理特征分类并统计其直方图。最后使用SVM支持向量机对纹理特征进行分类并计算分类的准确度。
实验部分图片如图所示:
Phthon代码
实验环境:Anaconda+jupyter notebook+python3.7
实验准备:将数据集文件Picture与lbp_classify.ipynb放入同一个文件下,打开jupyter notebook运行程序。
数据及所有代码见网盘:链接:https://pan.baidu.com/s/1fxXRGnFpnBQYFrGQ1YNq2w
提取码:4oeh
In [1]:
def loadPicture():
train_index = 0;
test_index = 0;
train_data = np.zeros( (200,171,171) );
test_data = np.zeros( (160,171,171) );
train_label = np.zeros( (200) );
test_label = np.zeros( (160) );
for i in np.arange(40):
image = mpimg.imread('picture/'+str(i)+'.tiff');
data = np.zeros( (513,513) );
data[0:image.shape[0],0:image.shape[1]] = image;
#切割后的图像位于数据的位置
index = 0;
#将图片分割成九块
for row in np.arange(3):
for col in np.arange(3):
if index<5:
train_data[train_index,:,:] = data[171*row:171*(row+1),171*col:171*(col+1)];
train_label[train_index] = i;
train_index+=1;
else:
test_data[test_index,:,:] = data[171*row:171*(row+1),171*col:171*(col+1)];
test_label[test_index] = i;
test_index+=1;
index+=1;
return train_data,test_data,train_label,test_label;
In [2]:
radius = 1;
n_point = radius * 8;
def texture_detect():
train_hist = np.zeros( (200,256) );
test_hist = np.zeros( (160,256) );
for i in np.arange(200):
#使用LBP方法提取图像的纹理特征.
lbp=skft.local_binary_pattern(train_data[i],n_point,radius,'default');
#统计图像的直方图
max_bins = int(lbp.max() + 1);
#hist size:256
train_hist[i], _ = np.histogram(lbp, normed=True, bins=max_bins, range=(0, max_bins));
for i in np.arange(160):
lbp = skft.local_binary_pattern(test_data[i],n_point,radius,'default');
#统计图像的直方图
max_bins = int(lbp.max() + 1);
#hist size:256
test_hist[i], _ = np.histogram(lbp, normed=True, bins=max_bins, range=(0, max_bins));
return train_hist,test_hist;
In[3] :
import matplotlib.image as mpimg
import matplotlib.pyplot as plt
import numpy as np
from sklearn.multiclass import OneVsRestClassifier
from sklearn.svm import SVR
from skimage import feature as skft
train_data,test_data,train_label,test_label= loadPicture();
train_hist,test_hist = texture_detect();
svr_rbf = SVR(kernel='rbf', C=1e3, gamma=0.1);
OneVsRestClassifier(svr_rbf,-1).fit(train_hist, train_label).score(test_hist,test_label)实验结果如图所式:
由实验结果可知,改进的LBP算法能够较好的对图像的纹理特征进行分类,并能达到较好的准确率。
参考文献:
- T. Ojala, M. Pietikäinen, and D. Harwood (1994), "Performance evaluation of texture measures with classification based on Kullback discrimination of distributions", Proceedings of the 12th IAPR International Conference on Pattern Recognition (ICPR 1994), vol. 1, pp. 582 - 585.
- T. Ojala, M. Pietikäinen, and D. Harwood (1996), "A Comparative Study of Texture Measures with Classification Based on Feature Distributions", Pattern Recognition, vol. 29, pp. 51-59.
- M.Pietikinen,I.Ojala,and Z.Xu. Rotation-Invariant Textture ClassificationUsing Feature Distributions.Pattern Recognition.2000
- Ojala, T., Pietikäinen, M. and Mäenpää, T. (2002), Multiresolution Gray-scale and Rotation Invariant Texture Classification with Local Binary Patterns. IEEE Trans. Pattern Analysis and Machine Intelligence 24(7): 971-987.
- Guo Y, Zhao G & Pietikäinen M (2012) Discriminative features for texture description.Pattern Recognition, vol. 45, no. 10, pp. 3834-3843, 2012.
- Ahonen, T., Hadid, A. and Pietikäinen, M. (2006), Face Description with Local Binary Patterns: Application to Face Recognition. IEEE Trans. Pattern Analysis and Machine Intelligence 28(12):2037-2041.
- Pietikäinen, M., Hadid, A., Zhao, G. and Ahonen, T. (2011), Computer Vision Using Local Binary Patterns, Springer, 207 p.
- Tan X, Triggs B. Fusing Gabor and LBP Feature Sets for Kernel-Based Face Recognition[M]// Analysis and Modeling of Faces and Gestures. Springer Berlin Heidelberg, 2007:235-249.
- Zhang G, Huang X, Li S Z, et al. Boosting local binary pattern (LBP)-Based face recognition[C]// Chinese Conference on Advances in Biometric Person Authentication. Springer-Verlag, 2004:179-186.
- 黄非非. 基于LBP的人脸识别研究[D]. 重庆大学, 2009
- 刘豪, 杨永全, 郭仙草, et al. 用于纹理特征提取的改进的LBP算法[J]. 计算机工程与应用, 2014, 50(6):182-185.
- 刘丽,匡纲要.图像纹理特征提取方法综述[J].中国图象图形学报,2009(4):622-635
- 肖霄. 图像LBP特征提取的研究与应用[D]. 吉林大学, 2011.
- 刘松涛, 马新星, 李剑. 基于LBP的多光谱图像纹理特征提取方法[J]. 光电技术应用, 2013, 28(5):36-40.
- 徐东海, 赵宏, 叶西宁. 基于改进LBP的表情特征提取算法[C]// 上海市化学化工学会2010年度学术年会论文集(自动化专题). 2010.
- 徐胜军, 刘欣, 赵亮. 基于快速收敛LBP算法的图像分割[J]. 计算机应用, 2011, 31(8):2229-2231.
这是一篇自己学习的一个笔记,献给正在学习图像处理的你们,学习计算机专业是个漫长的过程,要学习的东西很多,加油,给自己,给你们,如果你觉得有用的话,点个赞鼓励一下我吧!