图解二叉堆：堆排序

前言

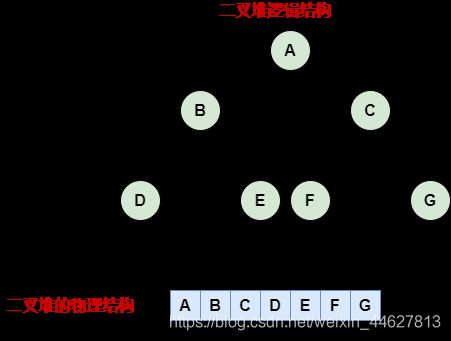
二叉堆和二叉树有什么关系呢？二叉堆的存储方式是数组，为什么我们总是把二叉堆画成二叉树呢？其实二叉堆是一种特殊的二叉树：完全二叉树。由于完全二叉树的性质所以我们更适合使用数组来存储，用数组的索引来操作子节点。而对于一般二叉树我们使用指针来操作子节点。其实二叉堆的主要核心操作就是down(下沉)和up(上浮)。

二叉堆的概念

下图是一个二叉堆实例。

---

从图上我们可以看出父亲和儿子节点索引的关系

int parent(int root){
     
	return (root-1)/2;//记住一定是先减1再除2
}
int leftChild(int root){
     
	return root*2+1;
}
int rightChild(int root){
     
	return root*2+2;
}

二叉堆的性质

■ 大根堆：每个节点都大于等于它的两个子节点，其中堆顶为堆中最大元素。
■ 小根堆：每个节点都小于等于它的两个子节点，其中堆顶为堆中最小元素。
■ 堆总是一棵完全二叉树。

其实大根堆和小根堆的核心思路都是一样的，就本文而言我就以小根堆来进行讲解。

实现 down 和 up

为什么会有下沉 down 和上浮 up 操作呢？就是为了维护堆的性质不变。我讲解的是最小堆(每个节点都小于等于它的两个子节点，其中堆顶为堆中最小元素)。但是当要插入和删除节点时，就会破坏堆之前保持的性质，所以才会有这两个操作。

使用down和up的情况：

■ 当某个堆中的某个节点大于它的任何一个子节点，那么自己就应该下沉下去，让更小的儿子到堆顶来维持堆的性质。使用down操作。
■ 当某个堆中的某个节点小于它的父亲节点，那么自己就应该上浮上去，让自己到堆顶来维持堆的性质。使用up操作。

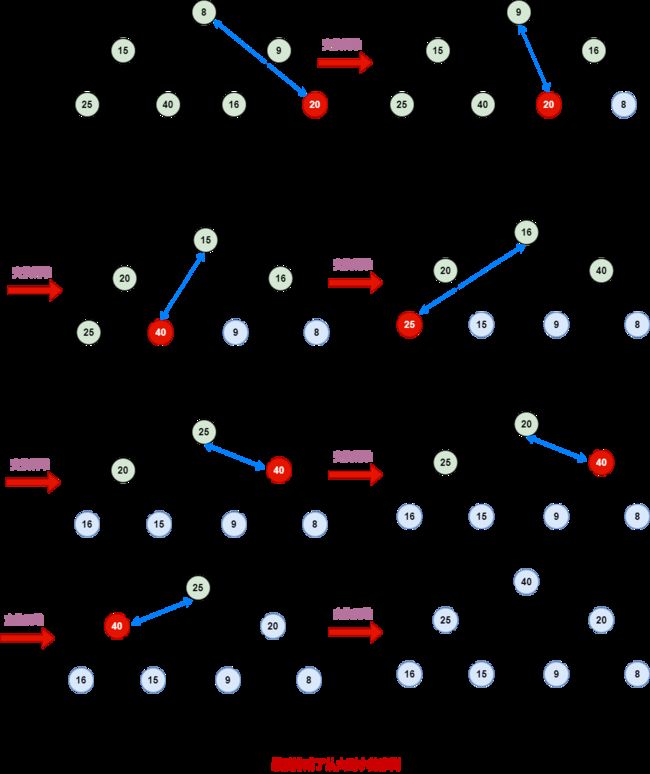
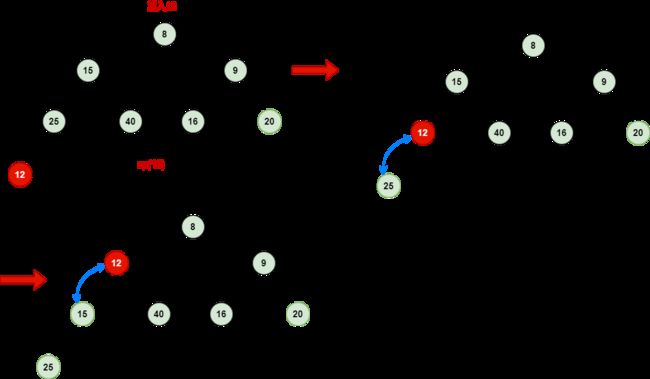
下图是一个使用down操作让节点达到正确位置的实例。

---

---

//迭代版本代码
void down(int *arr,int length,int child) {
     
	int parent = child;
	int child = 2 * parent + 1;
	//因为可能会调整多次才能到达正确的位置所以用while循环
	while (child < length) {
     //当child没有超过数组长度时就进行循环
		if (child + 1 < length && arr[child] > arr[child + 1]) child++;//child是左儿子，child+1是右儿子，这段代码找出儿子中最小的儿子
		if (arr[child] < arr[parent]) {
      //当儿子比父亲小时就将父亲下沉
			swap(arr[parent],arr[child]);
			parent = child; //继续将元素向下调整
			child = 2 * parent + 1;
		}else{
     
			break;	//当儿子不比父亲小说明已经保持了堆形态了就跳出循环
		}
	}
}
//递归版本代码
void down(int* arr, int length, int parent) {
     
	int temp = parent;
	if (2 * parent + 1 < length && arr[2 * parent + 1] < arr[temp])temp = parent * 2 + 1;
	if (2 * parent + 2 < length && arr[2 * parent + 2] < arr[temp])temp = 2 * parent + 2;
	if (temp != parent) {
     
		swap(arr[temp],arr[parent]);
		down(arr,length,temp);
	}
}

对于 down 下沉操作主要核心思想就是找两个儿子中的最小元素，如果自己比最小儿子大自己就和最小儿子交换，自己到最小儿子的位置，然后向下继续判断。

下图是一个使用 up 操作让节点达到正确位置的实例。

---

---

void up(int* arr,int child) {
     
	while ((child - 1)/2>0&arr[(child-1)/2]<arr[child]) {
      //如果父亲节点比自己大自己就应该上浮
		swap(arr[child],arr[(child-1)/2]);
		child = (child - 1) / 2;
	}
}

可以看到对于 up 上浮操作还是比较简单的，主要就是一直和自己的父亲节点比较，如果比父亲节点小就和父亲节点交换，然后自己到父亲节点的位置接着向上比较。

堆排序

堆排序就是基于 down 操作为核心来实现的。

■建堆：从最后一个非叶子节点开始到第一个非叶子节点建堆。

■调堆：从堆顶开始在剩下的数组中调堆。

建堆：从最后一个非叶子节点开始到第一个非叶子节点建堆。

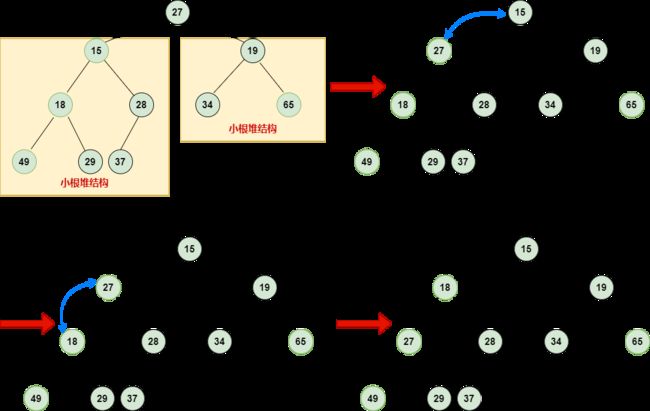
为什么从最后一个非叶子节点开始到第一个非叶子节点建堆，而不是从第一个非叶子节点到最后一个非叶子节点建堆？

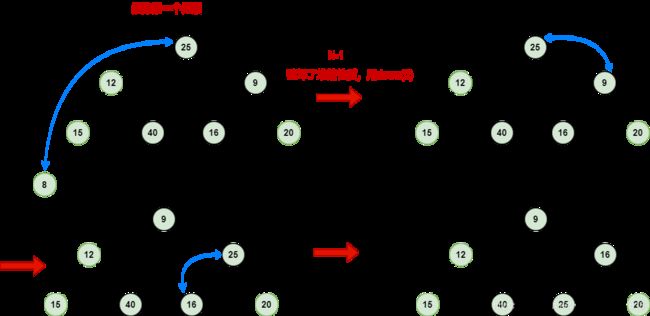
下图是从前往后建堆和从后往前建堆的比较。

---

总结：1.从后往前建堆，保证了每次的左右儿子节点已经是最小堆了，当父亲节点加入时，只需要donw一次操作，就能使父亲节点加入后成为一个更大的堆。最小元素一直往堆顶调，所以建完堆后最小元素就在第一个，满足最小堆的性质。2.从前往后建堆，不能保证当前堆的堆顶元素是当前堆中的最小元素，所以建堆完成之后不具有最小堆的性质。

建堆代码

//建堆
//length-1:最后一个节点的下标
//(length-1-1)/2:求的是最后一个非叶子节点的下标
for (int i = (length - 1 - 1) / 2; i >= 0; i--) {
     
	down(arr,length,i);
}

建堆时间复杂度

假设高度为 h，则从倒数第二层右边的节点开始，这一层的节点都要执行子节点比较然后交换（如果顺序是对的就不用交换）；倒数第三层呢，则会选择其子节点进行比较和交换，如果没交换就可以不用再执行下去了。如果交换了，那么又要选择一支子树进行比较和交换，一直重复下去；最坏情况下就是父亲节点要和所有的子节点进行比较。

---

---

建堆时间复杂度T(n) ≈ N ==>O(N)

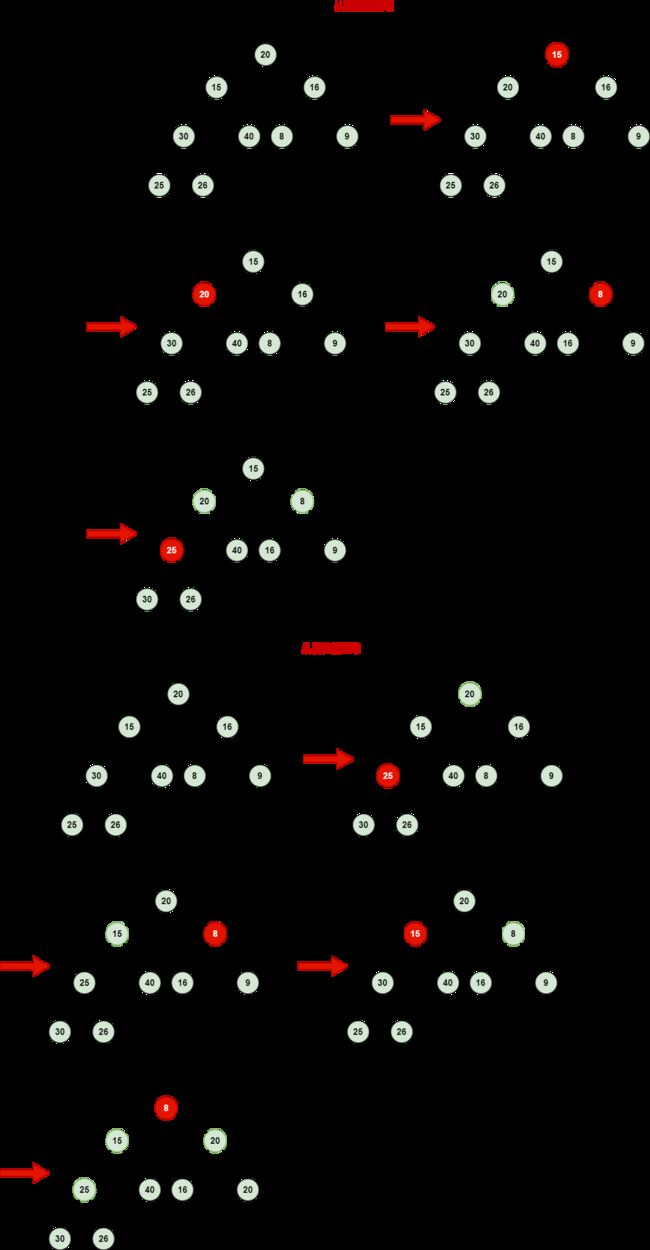
调堆：从堆顶开始在剩下的数组中调堆。

■ 将第一个元素换到和剩余数组最后一个元素交换，数组大小减一
■ 把堆中第一元素进行down操作，在剩余数组中进行调堆操作

下图是调堆的过程：

---

调堆代码

for (int i = length - 1; i > 0; i--) {
     
	swap(arr[i],arr[0]);
	down(arr,i,0);//将堆顶在剩余数组中执行down操作
}

总结：当我们要使用堆排序把数组排成从大到小的序列时，我们使用小根堆。我们想让数组从小到大排序时，我们使用大根堆进行排序。因为我们是让第一个元素和最后一个元素进行交换。

整体时间复杂度

调堆时间复杂度：以最坏的时间复杂度计算，以最后一层的元素计算一次调堆操作时间是：logN。有(N-1)个元素所以T(n)=(N-1)logN。
对于整体时间复杂度：T(N)<=O(建堆)+O(调堆)=N+(N-1)logN。因为在调堆时N的大小一直减小，所以总的时间复杂度小于N+(N-1)logN。最后T(N)≈NlogN。

实现 HeapPush和 HeapPop

其实这两个方法很简单，这两个方法是建立在 down 和 up 上实现的。

HeapPush方法：先将元素添加到数组最后一个位置然后让元素上浮到正确的位置。

---

HeapPush代码实现

void HeapPush(int key) {
     
	heap[N] = key;
	up(heap,N);
	N++;
}

HeapPop方法：如果我们直接将第一个元素删除不好删除，但是我们可以考虑将最后一个元素删除，那么我们将第一个元素和最后一个元素交换，此时将数组的大小减一，就删除了第一个元素，让第一个元素下沉到对应的位置。

HeapPop代码实现

void HeapPop(){
     
	N--;
	swap(heap[N],heap[0]);
	down(heap,0);
}

总结

二叉堆的核心操作其实就是 down 和 up 操作，相对来说 down 操作可能要难一些，但是熟悉了也还好。二叉堆的应用有：堆排序，TopK问题以及中位数。本文讲解了堆排序，下期我将介绍TopK问题和中位数，还有STL中的优先级队列底层也是使用二叉堆实现的。