数学建模算法与程序（司守奎）：第二章 整数规划

1概论

1.1定义

1.2.1整数规划的分类

1. 变量全限制为整数时，称纯（完全）整数规划。
2. 变量部分限制为整数的，称混合整数规划。

1.2.2整数规划的特点

(1)原线性规划有最优解，当自变量限制为整数后，其整数规划解出现在下述情况：
①原线性规划最优解全是整数，则整数规划最优解，与线性规划最优解一致。
②整数规划无可行解。
③有可行解（当然就存在最优解），但最优解值变差。
(2)整数规划最优解不能按照实数最优解简单取整而获得

1.3求解方法和分类

2分支定界法

对有约束条件的优化问题（其可行解为有限数）的所有可行解空间恰当地进行系统搜索，这就是分枝与定界内容。通常，把全部可行解空间反复地分割为越来越小的子集，称为分枝；并且对每个子集内的解集计算一个目标下界（对于小值问题），这称 为定界。在每次分枝后，凡是界限超出已知可行解集目标值的那些子集不再进一步分枝，这样，许多子集可不予考虑，这称剪枝。这就是分枝定界法的主要思路。

MODEL:
  SETS:
     col/1..2/:c,x;
     row/1..2/:b;
     links(row,col):a;
  ENDSETS
  DATA:
     C=40 90;
     a=9 7 7 20;
     b=56 70; 
  ENDDATA
  MAX=@SUM(col:c*x);
  @FOR(row(i):@SUM(col(j):a(i,j)*x(j))<b(i));
END

解：（1）先不考虑整数限制，解相应的线性规划B，得最优解为：
$$x_1=4.8092,x_2=1.8168,z=355.8779$$

可见它不符合整数条件。
这时z是问题A的最优目标数值的上界，而x
₁=0，x₂=0显然是问题A的一个整数可行解。即0≤z^*≤356

（2）因为x₁，x₂当前均为非整数，故不满足整数要求，任选一个进行分枝。
设选x₁进行分枝，把可行集分成2个子集：
x₁≤[4.8092]=4,x₁≥[4.8092]+1=5
因为4与5之间无整数，故这两个子集的整数解必须与原可行集合整数解一致。
这一步称为分枝。
问题B₁：lingo程序：

MODEL:
  SETS:
     col/1..2/:c,x;
     row/1..2/:b;
     links(row,col):a;
  ENDSETS
  DATA:
     C=40 90;
     a=9 7 7 20;
     b=56 70; 
  ENDDATA
  MAX=@SUM(col:c*x);
  @FOR(row(i):@SUM(col(j):a(i,j)*x(j))<b(i));
  x(1)<4;
END

问题B₂：lingo程序

MODEL:
  SETS:
     col/1..2/:c,x;
     row/1..2/:b;
     links(row,col):a;
  ENDSETS
  DATA:
     C=40 90;
     a=9 7 7 20;
     b=56 70; 
  ENDDATA
  MAX=@SUM(col:c*x);
  @FOR(row(i):@SUM(col(j):a(i,j)*x(j))<b(i));
  x(1)>5;
END

再定界：0≤z^*≤349

（3）对问题B₁再次进行分枝得问题B₁₁和B₁₂，它们的最优解为
B₁₁：x₁=4，x₂=2，z₁₁=340
B₁₂：x₂=1.43，x₂=300，z₁₂=327.14
再定界：340≤z^*≤341，并将B₁₂剪枝。

（4）对问题B₂再进行分枝得问题B₂₁和B₂₂，它们的最优解为
B₂₁：x₁=5.44，x₂=1.00，z₂₂=308
B₂₂无可行解

将B₂₁，B₂₂剪枝。
于是可以断定原问题的最优解为：
x₁=4，x₂=2，z*=340

3 0-1型整数规划

0-1型整数规划是整数规划中的特殊情形，它的变量x_j仅取值0或1。这时x_j称为0-1变量，或称二进制变量。x_j仅取值0或1这个条件可由下述约束条件：
$$0\le x_j\le 1，整数$$
所代替，是和一般整数规划的约束条件形式一致的。在实际问题中，如果引入0-1变量，就可以把有各种情况需要分别讨论的线性规划问题统一在一个问题中讨论了。

3.1 引入0-1变量的实际问题

3.1.1 投资场所的选定——相互排斥计划

eg4.某公司拟在市东、西、南三区建立门市部。拟议中有7个位置(点)A_i（i=1,2,…,7）可供选择。规定：

在东区。由A₁,A₂,A₃三个点中至多选两个；
在西区。由A₄,A₅两个点中至少选一个；
在南区，由A₆，A₇两个点中至少选一个。

如选用A_i点，设备投资估计为b_i元，每年可获利润估计c_i元，但总投资额不能超过B元。问应选择哪几个点可使年利润为最大?

3.1.2相互排斥的约束条件

有两个排斥的约束条件
约束条件
$$x_1=0或500\le x_1\le 800$$

可改写为

3.1.3关于固定费用的问题

在讨论线性规划时，有些问题是要求使成本为最小。那时设固定成本为常数，并在线性规划模型中不必明显列出。
但有些固定费用（固定成本）的问题不能用一般线性规划来描述，但可改变为混合整数规划来解决。
$x_j表示采用第j种方式的产量；$
$c_j表示采用第j种方式时每件产品的变动成本；$
$k_j表示采用第j种方式时的固定成本。$

为了说明成本的特点，暂时不考虑其他约束条件。采用各种生产方式的总成本分别为：
在构成目标函数时为了统一在一个问题中讨论，现在引入0-1变量y_j，令

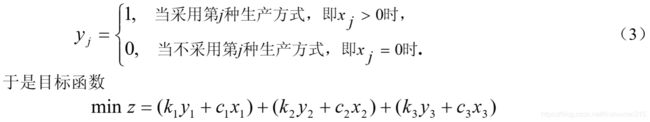
3.2 0-1型整数规划解法之一（过滤隐枚举法）

求解思路及改进措施：
（i）试探：先试探性地求一个可行解，易看出(x₁,x
₂,x₃)=(1,0,0)满足约束条件，故为一个可行解，且z=3。
（ii）增加条件：因为是求极大值问题，故求最优解时，凡是目标值z＜3的解不必检验是否满足约束条件即可删除，因为它肯定不是最优解，于是应增加一个约束条件（目标值下界）：
（iii）改进：改进过滤条件。
（iv）提高过滤门槛：由于每个组合首先计算目标值以验证过滤条件，故应优先计算目标值z大的组合，这样可以抬高过滤门槛，以减少计算量。

4 蒙特卡洛法（随机取样法）

用蒙特卡洛去随机计算10⁶个点，便可找到满意解。
这种方法的可信度可以用如下方法表示：
假设目标函数落在高值区的概率分别为0.01，0.00001,当计算10⁶个点后，有任意一个点能落在高值区的概率为：
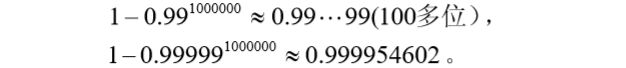matlab求解：
（i）先编写M文件mengte.m定义f和约束向量函数g，程序如下：

function [f,g] = mengte(x)
f=x(1)^2+x(2)^2+3*x(3)^2+4*x(4)^2+2*x(5)-8*x(1)-2*x(2)-3*x(3)-x(4)-2*x(5);
g=[sum(x)-400
    x(1)-2*x(2)+2*x(3)+x(4)+6*x(5)-800 
    2*x(1)+x(2)+6*x(3)-200 
    x(3)+x(4)+5*x(5)-200]; 
end

（ii）编写M文件mainint.m如下求问题的解

rand('state',sum(clock));
p0=0;
tic
for(i=1:10^6)
    x=99*rand(5,1);%随机取5行1列的矩阵
x1=floor(x);%x1为x的向下取整
x2=ceil(x);%x2为x的向上取整
[f,g]=mengte(x1);%通过随机生成的向下取整的x1求出f和g
if sum(g<=0)==4%如果符合整数规划的要求
    if p0<=f%如果p0是更好的解要求
        x0=x1;p0=f;%则用x0代替现在的x1，用p0代替f
    end
end
[f,g]=mengte(x2);
if sum(g<=0)==4
    if p0<=f
        x0=x2;p0=f;
    end
end
end
disp(strcat('x0的值为',num2str(x0)))
disp(strcat('p0的值为',num2str(p0)))
toc

本题可以使用LINGO软件求得精确的全局最优解：

MODEL:
  SETS:
     row/1..4/:b;
     col/1..5/:c1,c2,x;
     links(row,col):a;
  ENDSETS
  DATA:
    c1=1,1,3,4,2;
    c2=-8,-2,-3,-1,-2;
    a=1 1 1 1 1
      1 2 2 1 6
      2 1 6 0 0
      0 0 1 1 5;
    b=400,800,200,200;
  ENDDATA
  max=@sum(col:c1*x^2+c2*x); 
  @for(row(i):@sum(col(j):a(i,j)*x(j))<b(i)); 
  @for(col:@gin(x)); 
  @for(col:@bnd(0,x,99));
END

5 指派问题的计算机求解

整数规划问题的计算机求解
整数规划问题的求解可以使用lingo等专用软件。
对于一般的整数规划问题，无法直接利用Matlab的函数，必须利用Matlab编程实现分枝定界和割平面解法。
但对于指派问题等0-1整数规划问题，可以直接利用matlab的函数bintprog进行求解。

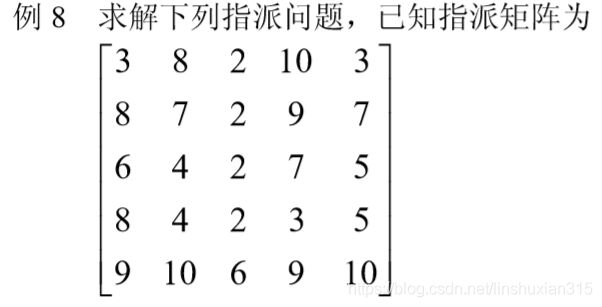
编写matlab程序如下：

c=[3 8 2 10 3;8 7 2 9 7;6 4 2 7 5
   8 4 2 3 5;9 10 6 9 10];
c=c(:);
a=zeros(10,25);
for i=1:5
   a(i,(i-1)*5+1:5*i)=1;
   a(5+i,i:5:25)=1;
end
intcon=[1:5];
b=ones(10,1);
lb = zeros(25,1);
ub = ones(25,1);
[x,y]=intlinprog(c,intcon,[],[],a,b,lb,ub);
x,y

lingo程序求解：

MODEL:
  SETS:
     var/1..5/;
     link(var,var):c,x;
  ENDSETS
  DATA:
    c=3 8 2 10 3
     8 7 2 9 7
     6 4 2 7 5
     8 4 2 3 5
     9 10 6 9 10;
  ENDDATA
  min=@sum(link:c*x); 
  @for(var(i):@sum(var(j):x(i,j))=1);
  @for(var(j):@sum(var(i):x(i,j))=1);
  @FOR(link:@bin(x));!0-1限制;
END

6 生产与销售计划问题

6.1问题实例

6.2建立模型

（1）问题分析
目标：利润最大。
题目所给条件：
①两种汽油的售价②原油A的采购价③利润为销售汽油的收入与购买原油A的支出之差。
难点：原油A的采购价与购买量关系比较复杂，是分段函数关系，能否及如何用线性规划、整数规划模型加以处理是关键所在。
（2）模型建立
设原油A的购买量为x（单位：吨），根据题目所给数据，采购支出c(x)可表示如下的分段线性函数（以下价格以千元/吨为单位）：
设原油A用于生产甲、乙两种汽油的数量x₁₁和x₁₂，原油B用于生产甲、乙两种汽油的数量分别为x₂₁、x₂₂，则总的收入为4.8(x₁₁+x₂₁)+5.6(x₂₁+x₂₂)（千元）。于是本例的目标函数利润为（利润）为

遇到的问题： 由于（5）式中的c(x)不是线性函数，（5）~（12）给出的是一个非线性规划，而且，对于这样的分段函数定义的c(x)，一般的非线性规划软件也难以输入和求解。

解决办法：必须把该模型化简，从而实现软件求解。

6.3求解模型

下面介绍三种方法：
（1）解法一：
将原油A的采购量x分解为三个量，即用x₁，x₂，x₃分别表示以价格10千元/吨、8千元/吨、6千元/吨采购的原油A的吨数，总支出为c(x)=10x₁+8x₂+6x₃,且

采用lingo软件求解：

MODEL:
  SETS:
    var1/1..4/:y;!这里y(1)=x11,y(2)=x21,y(3)=x12,y(4)=x22;
    var2/1..3/:x,c;
  ENDSETS
  
  DATA:
    c=10 8 6;!c(x)=10x1+8x2+6x3;
  ENDDATA

  max=4.8*(y(1)+y(2))+5.6*(y(3)+y(4))-@sum(var2:c*x);
  y(1)+y(3)<@sum(var2:x)+500;!x11+x12≤500+x;
  y(2)+y(4)<1000;!x21+x22≤1000;
  0.5*(y(1)-y(2))>0;!(10)式子;
  0.4*y(3)-0.6*y(4)>0;!(11)式子;
  (x(1)-500)*x(2)=0;!A的进货量表示;
  (x(2)-500)*x(3)=0;!A的进货量表示;

  @for(var2:@bnd(0,x,500));
END

（2）解法二

引入0-1变量将（15）和（16）转化为线性约束
令z₁，z₂,z₃=1分别表示以10千元/吨、8千元/吨、6千元/吨的价格采购原油A，则约束(15)和(16)可替换为：
式(7)~(14)，式子(17)~（21）构成混合整数线性规划模型，将它输入LINGO软件：

model: 
sets:   
var1/1..4/:y;  !这里y(1)=x11,y(2)=x21,y(3)=x12,y(4)=x22;     
var2/1..3/:x,z,c; 
endsets 
max=4.8*(y(1)+y(2))+5.6*(y(3)+y(4))-@sum(var2:c*x); 
y(1)+y(3)<@sum(var2:x)+500; 
y(2)+y(4)<1000; 
0.5*(y(1)-y(2))>0; 
0.4*y(3)-0.6*y(4)>0; 
@for(var1(i)|i #lt# 3:500*z(i+1)<x(i);x(i)<500*z(i)); 
x(3)<500*z(3); 
@for(var2:@bin(z)); 
@for(var2:@bnd(0,x,500)); 
data: 
c=10 8 6; 
enddata 
end 

（3）解法三
直接处理分段函数$c(x)$
式（5）表示的函数$c(x)$如图1所示。
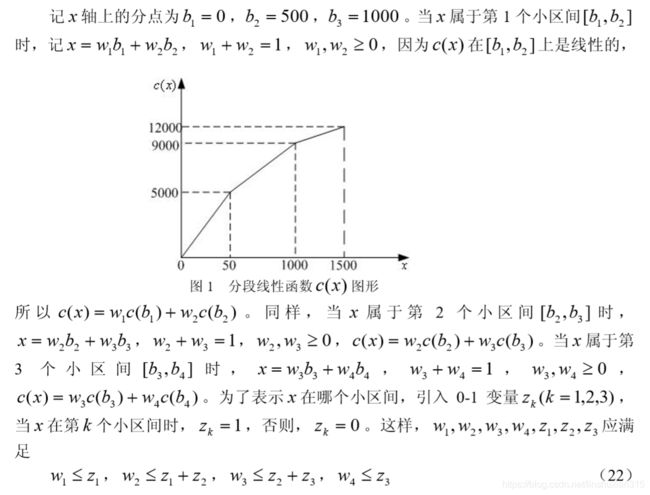
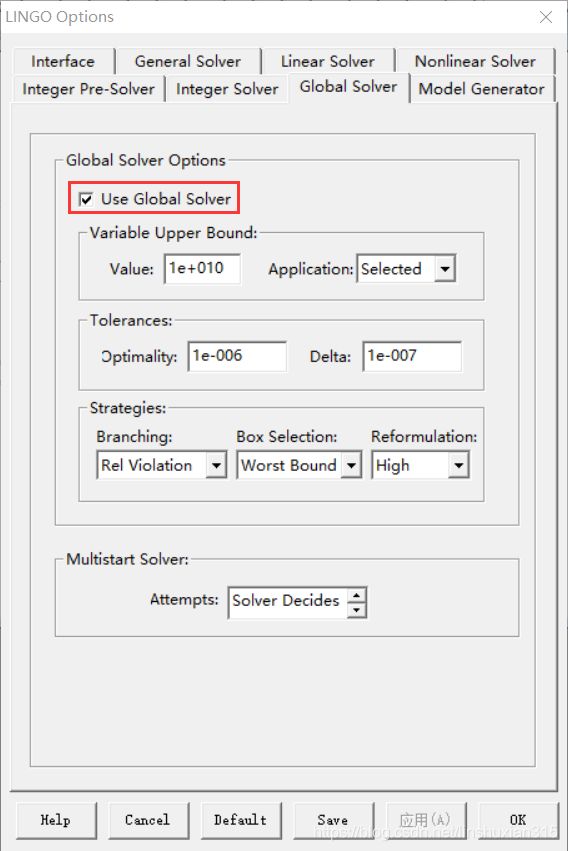
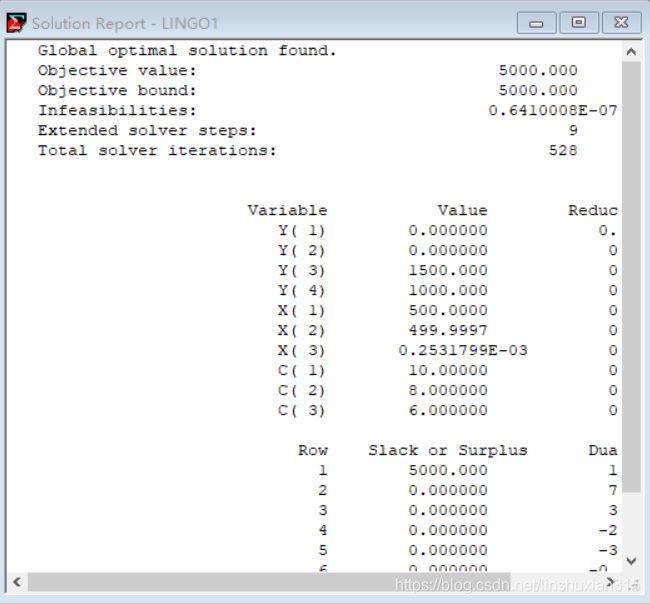
LINGO 求解。输入的 LINGO 模型如下：

model:
sets:
 var/1..4/:b,c,y,z,w;  !这里y(1)=x11,y(2)=x21,y(3)=x12,y(4)=x22   端点数为4，即分段数为3; 
endsets 
data: 
b=0,500,1000,1500; 
c=0,5000,9000,12000; 
z=,,,0;   !增加的虚拟变量z(4)=0; 
enddata 
max=4.8*(y(1)+y(2))+5.6*(y(3)+y(4))-@sum(var:c*w); 
y(1)+y(3)<@sum(var:b*w)+500; 
y(2)+y(4)<1000; 
0.5*(y(1)-y(2))>0; 
0.4*y(3)-0.6*y(4)>0; 
w(1)<z(1); 
@for(var(i)|i #ne# 1:w(i)<z(i-1)+z(i)); 
@sum(var:z)=1; 
@sum(var:w)=1; 
@for(var:@bin(z)); 
End 

注：这个问题的关键是处理分段线性函数，我们推荐化为整数线性规划模型的第2和第3种解法，第3种解法更具一般性，其做法如下。