斯坦福机器学习笔记01 - 线性回归和梯度下降

机器学习的定义

机器学习

不通过具体编程，使计算机获得学习能力的学科。

监督学习（Supervised Learning）

用于训练的数据已经有标签。具体分为回归问题（regression）和分类问题（classification）。

无监督学习（Unsupervised Learning）

与监督学习相对，数据没有标签，所以只能对于数据进行分类，将相似的分到一起。经典案例是聚类分析。

强化学习（Reinforcement Learning）

通过定义回报（reward），引导程序趋利避害，做出正确的决策。

线性回归

假设我们希望通过房屋面积x预测房价y，训练数据的形式如下：

面积	价格
100	1001
200	2001
105	1050
…	…

能够想到的最简单的数学模型就是线性模型：

hθ=θ0+θ1x

使用模型的通用方法

无论使用何种模型，使用该模型进行机器学习的一般方法是：
1. 随机（或使用其他方法）初始化模型参数
2. 建立误差函数
2. 使用梯度下降（或类似方法），找到最小误差对应的模型参数

误差函数

假设我们已经随机初始化了参数 θ0,θ1 ，如何使用训练数据集来改善 θ0,θ1 的值呢？对于任意一个训练数据 (xi,yi) ，我们可以用预测值和实际值的距离来表示我们现有模型的误差，即 (hθ(xi)−yi)2 。而现有对于全部训练值的误差，则可以表示为如下误差函数：

J(θ0,θ1)=12n∑i=0n(hθ(xi)−yi)2

其中，n为训练数据集的大小，而 12 则是为了求导计算方便。

梯度下降

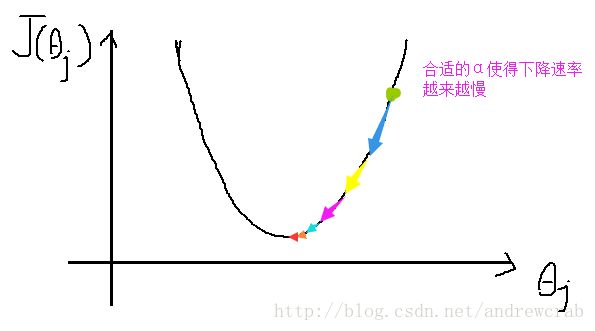
梯度下降的基本概念可以表述为下图，假设有误差函数 J(θj) ，在初始化后，我们落在最低点右侧。

梯度下降的基本方法是计算我们现在所在的 θj 点的坡度，然后向坡度下降方向走一小步。重复这一步骤直至走到最低点，到达这一点后再走则都是向上的了，函数到这里就收敛了。

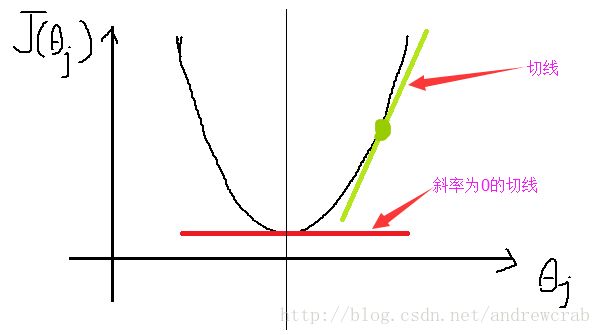
下面我们研究如何进行计算。假设我们初始化的值在点 θj ，为了确定坡度，可以对误差函数进行求导，即 ∂∂θjJ(θ0,θ1) 。如果如图所示，导数大于零，则表示目前该点在最小值的右侧，则我们应该向左走一小步。

上述操作可以表述为 θj:=θj−αddθjJ(θj) 。这里，我们使用学习速率来控制每一步的幅度。 α 是一个介于0,1间的常数。

对于线性回归的误差函数，则可以使用偏导数表示：

θj:=θj−α∂∂θjJ(θ0,θ1)

将 J(θ0,θ1)=12n∑ni=0(hθ(xi)−yi)2 带入上式，可得:

θ0:=θ0−α1n∑i=0n(hθ(xi)−yi)

θ1:=θ1−α1n∑i=0n(hθ(xi)−yi)xi

重复上述步骤直至收敛，则可以得到使得误差函数最小的 θ0,θ1 。

注意事项

• 在使用上述公式更新 θ0,θ1 时，必须同时更新两者，如果先更新 θ0 ，再更新 θ1 ，则 θ1 会使用更新后的 θ0 ，造成错误。
• α 值不需要在计算的过程中进行调整。在趋近于最低点时，导数会无限趋近于零，则更新幅度会无限趋近于零。所以在更新的过程中，更新幅度会越变越小。
• 学习速率过大会造成函数无法收敛。

多元线性回归

和一元线性回归类似，多元线性回归可以表示为 hθ(x)=θ0+θ1x1+...+θnxn ，还可表示为 hθ(x)=θ0x0+θ1x1+...+θnxn,x0=1 , 或 hθ(x)=∑ni=0θixi ，或 hθ(x)=θTX 。

参考上文，多元线性回归的梯度下降函数可以表示为：

θn:=θn−α1n∑i=0n(hθ(x(i))−y(i))x(i)n

注意事项

学习速率

为选择合适的学习速率 α ，一般使用实验的方法，具体可以选择数个学习速率，每一个为前一个的3倍，如： …, 0.001, 0.003 , 0.01, 0.03, 0.1, 0.3…，学习速率过小会使学习过程很慢，过大则可能不会收敛。

数据标准化 （Normalization）

数据过大会减慢学习的速度，一般希望每个特征数据均是以零为均值，并介于-1，1之间。在开始训练前需要首先对数据进行标准化。

逻辑回归（Logistic Regression）

假设我们希望通过肿瘤的直预测该肿瘤是否为良性。我们收集的数据为肿瘤直径x，和肿瘤性质y，其中，y=1表示肿瘤为恶性，反之则为良性。这是一个典型的二分类问题。

基本模型

我们希望使用已经掌握的线性回归方法解决上述分类问题。假设有线性函数 hθ(x)=θTX ，如果 hθ(x)>0.5 则肿瘤为恶性，即1。通过这种方法，就可以使用线性回归的方法解决分类的问题。具体方法可以参考下图：

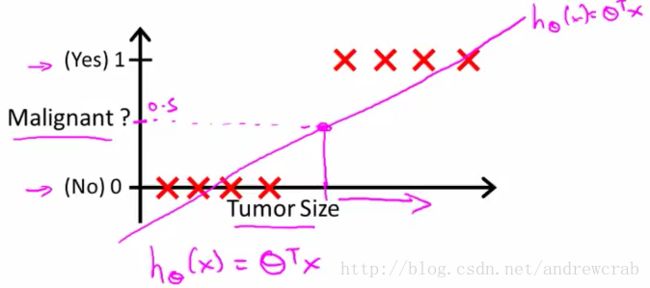
但是，线性回归方法的问题是其预测值会远超过（0，1）的范围，我们希望将函数的预测值控制在（0，1）的范围就需要使用logit 函数，这也就是lotistic regression的名称由来。该函数的公式和图像如下：

g(z)=11+e−z

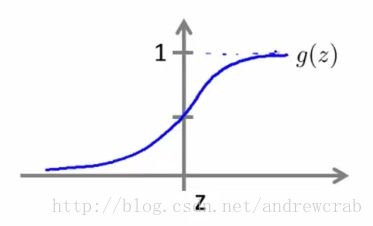
则上述多元线性模型可改写为

hθ(x)=g(θTX)

该函数求出的是（0,1）间的一个值，可以理解为属于类别1的概率，确定具体的分类为0或1，则需要将上式求出的值带入下式：

y={ y=1,hθ(x)≥0.5y=0,hθ(x)<0.5

误差函数

因为误差函数 J(θ0,θ1)=12n∑ni=0(hθ(xi)−yi)2 在分类中使用时不是一个严格的凹方程，有很多局部最小值，所以我们将要使用下列方程：

Cost(hθ(x),y)={ −log(hθ(x)),ify=1−log(1−hθ(x)),ify=0

在该误差函数中，若y=1，则有下列图像。在预测值 hθ(x) 和y值相近时，误差无限趋近于0，在预测值和y不相符，即趋近于0是，误差趋近于无限。

为了方便求导，上述公式可以改写为：

Cost(hθ(x),y)=−ylog(hθ(x))−(1−y)log(1−hθ(x))

多个类别分类

分类n个类别的方法（One-vs-All）是建立在两个类别的基础之上的，即建立n个逻辑回归模型。在研究类别i，认为其他所有数据属于另一类别k，然后使用逻辑回归的方法进行计算。全部计算完成后，取 hθ(x) 最大的一类。

正则化

过拟合

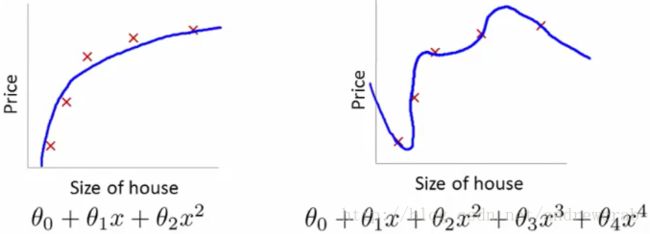
假设我们使用函数 y=x2+x+1 模拟了一系列房屋面积和价格数据，并加入了一些随机噪音。下文左图展示了只需要三个参数即可准确预测。但右图中我们使用了五个参数，虽然对于训练数值集合，这样做误差更小，但对于没有模型没有见过的数据，则误差变得更大了，这种情况叫做过拟合。所以，过拟合是因为模型囊括了太多参数造成的。

L1正则化

因为过拟合是参数太多造成的，那么可以通过在误差参数后加上正则化参数的方法来抑制参数的增加:

λ∑j=1nθ2j

λ 称为正则化系数，λ越大则越多的 θ 值为零。

以线性规格为例，求导后，可得下列梯度下降公式：

θ0:=θ0−α1n∑i=0n(hθ(x(i))−y(i))x(i)nθn:=θn−α[1n∑i=0n(hθ(x(i))−y(i))x(i)n+λnθn]

该公式可以改写为：

θn:=(1−αλn)θn−α[1n∑i=0n(hθ(x(i))−y(i))x(i)n]

我们可以理解为，在每次赋值的过程中 θn 都会减少（向0的方向移动）一个固定比例 −αλnθn ，因此，如果导数过小，则 θn 会无限趋近于零。这样，只有较重要的 θn 会留下。

神经网络

SVM

参考
本文图片来源：
http://blog.csdn.net/artprog/article/details/51104192