机器学习--支持向量机(SVM)

引入

回忆LogisticRegression的思想，它最开始的思想是寻找一个超平面来把特征空间一分为二，然后两边各算一类。
那么问题就来了，对于一个能明确由一个超平面划分的特征空间，能把所有样本一分为二且能完美划分的超平面数肯定是有无限多个的，比如下面这种。

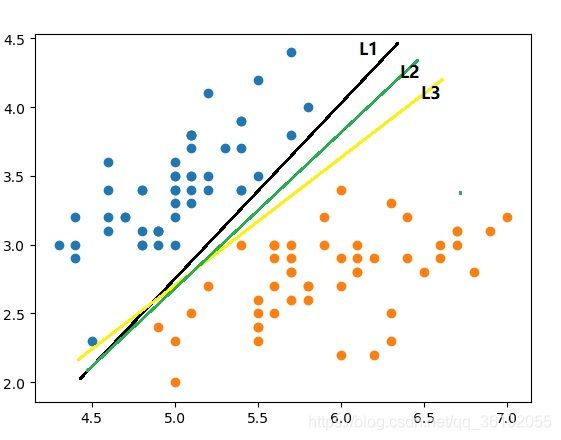
L1和L2和L3都可以把特征空间分成两部分，而且都完美的把所有的训练数据进行了分类，那么他们之间谁更好一点呢，此时就需要回到最开始类似于逻辑回归的想法中去。

函数间隔和几何间隔

设超平面为$w\ast \text{x}+b=0$，其中x是n维的向量，然后这个方程就代表了n维超平面。
假设已经得到了一个超平面$w^{\ast }\ast \text{x}+b^{\ast }=0$它可以划分特征空间，那么考虑这么一个事情，假设有两个点他们到达这个超平面的距离各不相同。

一个远一个近，想象一下如果有一个点会被分错，那么会是哪个？肯定是离得近的点因为超平面稍微移动一下他就可能会到另一类，所以可以说离超平面越远的点它的分类的可信度就越高。

所以，可以用点与超平面之间的距离来刻画这种可信程度。
首先现规定一下数据集$T=\{({\text{x}}_1,y_1),({\text{x}}_2,y_2)...({\text{x}}_n,y_n)\}$ 其中$y_i\in \{-1,1\}$
规定，超平面的法向量指向的那一边为正类即$y=1$，反之为反类$y=-1$

函数间隔

函数间距定义为$|w\ast \text{x}+b|$更直观的来看就是

观察标记与值的关系，可以发现上式还可以写成$y(w\ast \text{x}+b)$

几何间隔

函数间隔存在着一点的问题，比如只需要成倍的增加w和b就会使$y(w\ast \text{x}+b)$成倍的增加，所以这里需要对函数间隔进行进一步的限制。
我们把函数间隔除以向量$w$的模$||w||$即$\frac{y(w\ast \text{x}+b)}{||w||}$这个称为几何间隔
直观上的来看它长这样。

而上式正是点到直线距离的推广。

Hard Margin线性可分

首先做出一个假设，一定存在一个超平面可以把特征空间完美的一分为二，使所有的同类别的数据落在一边，而对于求解这种问题就叫做Hard Margin线性可分

回到上面的思路，既然样本点距离超平面越远可信度越高，那么只需要所有的样本点最近的那一个尽可能的远就可以了，这样的超平面的可信度肯定是最高的，同时在提高可信度的同时还应该保证这个超平面能够正确的完成分类，那么就得到了下面这个式子。
$$\begin{gathered} \underset{w,b}{\max }\gamma \\ s.t.\frac{y_i(w\ast {\text{x}}_i+b)}{||w||}\ge \gamma (i=1,2...,N) \end{gathered}$$
${\max }_{w,b}\gamma$即需要确定一个$w,b$使几何间隔$\gamma$最大化，同时又需要满足约束条件：
$$s.t.\frac{y_i(w\ast {\text{x}}_i+b)}{||w||}\ge \gamma (i=1,2...,N)$$
上面约束条件表明，所有的的样本都应该距离超平面至少$\gamma$.

设$\hat{\gamma }为\gamma$所对应的函数间距，即$\frac{\hat{\gamma }}{||w||}=\gamma$
则上式可以写成:
$$\begin{gathered} \underset{w,b}{\max }\frac{\hat{\gamma }}{||w||} \\ s.t.y_i(w\ast {\text{x}}_i+b)\ge \hat{\gamma }(i=1,2...,N) \end{gathered}$$
由于函数距离是可以随意成倍变动的，所以取$\hat{\gamma }=1$得：
$$\begin{gathered} \underset{w,b}{\max }\frac{1}{||w||} \\ s.t.y_i(w\ast {\text{x}}_i+b)\ge 1(i=1,2...,N) \end{gathered}$$
由于$\frac{1}{||w||}$趋近于最大值时和$\frac{1}{2}||w|{|}^2$趋近于最小值时是等价的，所以用求$\frac{1}{2}||w|{|}^2$的最小值代替求$\frac{1}{||w||}$的最大值，得：
$$\begin{gathered} \underset{w,b}{\min }\frac{1}{2}||w|{|}^2 \\ s.t.y_i(w\ast {\text{x}}_i+b)\ge 1(i=1,2...,N) \end{gathered}$$
然后移项不等式两边同时乘以-1得：
$$\begin{gathered} \underset{w,b}{\min }\frac{1}{2}||w|{|}^2 \\ s.t.1-y_i(w\ast {\text{x}}_i+b)\le 0(i=1,2...,N) \end{gathered}$$
这很很明显可以构造成一个拉格朗日函数(至于为什么，看我的这一篇文章这里)：
$$L(w,b,\alpha )=\frac{1}{2}||w|{|}^2-\sum _{i=1}^N{y}_i{\alpha }_i(w\ast {\text{x}}_i+b)+\sum _{i=1}^N{\alpha }_i$$
然后就可以写出它的对偶问题了：
$$\begin{gathered} \underset{w,b}{\min }\frac{1}{2}||w|{|}^2 \\ s.t.1-y_i(w\ast {\text{x}}_i+b)\le 0(i=1,2...,N) \\ 等价于求 \\ \underset{\alpha :{\alpha }_i\ge 0}{\max }\underset{w,b}{\min }L(w,b,\alpha ) \end{gathered}$$
所以问题转化成了求：
$$\underset{\alpha }{\max }\underset{w,b}{\min }L(w,b,\alpha )$$
第一步就是求$$\underset{w,b}{\min }L(w,b,\alpha )$$
首先就需要对$w,b$分别求偏导然后让他们分别等于0
得到：
$$\begin{gathered} w-\sum _{i=1}^N{\alpha }_i{y}_i{\text{x}}_i=0=>\sum _{i=1}^N{\alpha }_i{y}_i{\text{x}}_i=w \\ \sum _{i=1}^N{\alpha }_i{y}_i=0 \end{gathered}$$
然后把$w$和$\sum _{i=1}^N{\alpha }_i{y}_i=0$带入$L$函数，得到：
$$L(w,b,\alpha )=\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j({\text{x}}_i\cdot {\text{x}}_j)-\sum _{i=1}^N{\alpha }_i$$
于是对偶问题变成了求：
$$\begin{gathered} \underset{\alpha }{\max }-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j({\text{x}}_i\cdot {\text{x}}_j)+\sum _{i=1}^N{\alpha }_i \\ s.t.{\alpha }_i\ge 0(i=1,2...N) \end{gathered}$$
最后再把式子转变一下，把目标函数取反，转成求极小值
$$\begin{gathered} \underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j({\text{x}}_i\cdot {\text{x}}_j)-\sum _{i=1}^N{\alpha }_i \\ s.t.{\alpha }_i\ge 0(i=1,2...N) \end{gathered}$$
根据KKT条件得：
$$\begin{gathered} w^{\ast }=\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{\text{x}}_i \\ {b}^{\ast }=y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i({\text{x}}_i\cdot {\text{x}}_j)[{\alpha }_j^{\ast }>0] \end{gathered}$$
由此就得出了答案，只需要求出${\alpha }^{\ast }$就可以得出超平面的方程，而求解这个问题可以使用SMO算法。

支持向量

回到之前的推导出Hard Margin问题的思路，它的想法是让离超平面最近的点的距离尽可能的远，那么就会出现这种情况。

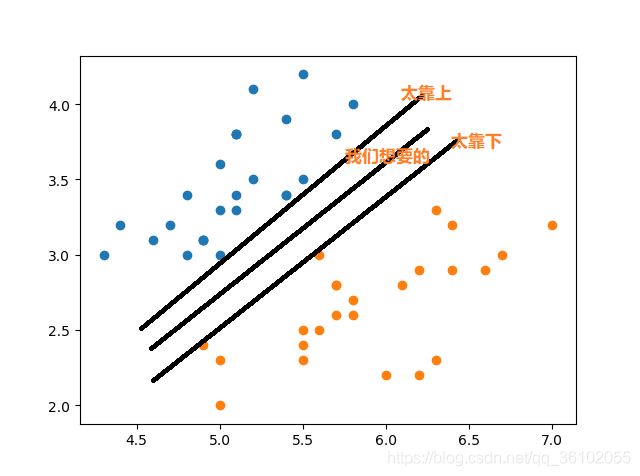
那种太靠上和靠下的极限情况就是离他们最近的点距离为0，此时就达到了极限情况，而支持向量机所求的最佳情况就夹在这两个上下平面的中间，所以这极少数的数据就是支持向量，由他们撑起来了两个超平面，因为最终的结果是由他们支撑起来的，显然的支持向量与最终所求的超平面平行。

假设已经求出超平面了，回到上面的原式问题$$\begin{gathered} \underset{w,b}{\min }\frac{1}{2}||w|{|}^2 \\ s.t.1-y_i(w\ast {\text{x}}_i+b)\le 0(i=1,2...,N) \end{gathered}$$
如果已经求出一组$w^{\ast },b^{\ast }$使$\frac{1}{2}||w|{|}^2$最小，那么此时一定有 $1-y_i(w^{\ast }\ast {\text{x}}_i+b^{\ast })\le 0(i=1,2...,n)$成立
那么也就存在一个点使等号成立，即达到边界（如果不存在那么说明此时不是最优，因为$\frac{1}{2}||w|{|}^2$还可以再小）
那么就有$1-y_i(w^{\ast }\ast \text{x}+b^{\ast })=0$
即$w^{\ast }\ast \text{x}+b^{\ast }=\pm 1$
此时就是满足约束条件的极限情况，也就是支持向量的所在位置。

Soft Margin线性可分

对于Hard Margin问题，经常无法找到适用的情况，因为噪声的原因导致并没有办法找到一个超平面完美的划分训练数据集，回到原始问题
$$\begin{gathered} \underset{w,b}{\min }\frac{1}{2}||w|{|}^2 \\ s.t.y_i(w\ast {\text{x}}_i+b)\ge 1(i=1,2...,N) \end{gathered}$$
可以看到在约束s.t.中所有的样本都大于函数距离1，这样就保证了所有的样本点到超平面的的距离不会超过某个值，但是也许可以改变一下，允许某些变量超过这个距离，也就是给模型一个犯错误的机会。
$$\begin{gathered} \underset{w,b}{\min }\frac{1}{2}||w|{|}^2 \\ s.t.y_i(w\ast {\text{x}}_i+b)\ge 1-{\xi }_i(i=1,2...,N，{\xi }_i\ge 0) \end{gathered}$$
加入一个$\xi$来使所有点不必都与超平面保持同一的距离，很明显$\xi$越大约束条件就越宽松，如果约束条件太宽松反而会大大降低模型的拟合程度，所以需要模仿正则化加入一项作为惩罚。
所以最终的优化变成了：
$$\begin{gathered} \underset{w,b}{\min }\frac{1}{2}||w|{|}^2+C\sum _{i=1}^N{\xi }_i \\ s.t.y_i(w\ast {\text{x}}_i+b)\ge 1-{\xi }_i(i=1,2...,N，{\xi }_i\ge 0) \end{gathered}$$
其中C就是惩罚系数，当C越小对$\xi$惩罚就越弱，C越大对$\xi$惩罚强，当C趋于正无穷时Soft Margin变为Hard Margin

支持向量

在求解Hard Margin的过过程中，使用了KKT条件得到了
$$\begin{gathered} w^{\ast }=\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{\text{x}}_i \\ {b}^{\ast }=y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i({\text{x}}_i\cdot {\text{x}}_j)[{\alpha }_j^{\ast }>0] \end{gathered}$$
其中${\alpha }_j^{\ast }\ge 0$这说明了，其实截距是由少数数据决定的，而这少数数据也正是支持向量，所以从推导上来看，也确实是极少数的数据决定了整个模型。
在Soft Margin中也是一样的，根据Hard Margin的思路，也可以得到其支持向量，那就是通过其${\alpha }_j$的超平面。

sklearn中的SVC

SVC即用于解决分类问题的SVM，全称为Support Vector Classification
可以从sklearn中的svm包导入LinerSVC然后创建实例
由于SVM算法需要计算距离，对于数据的大小十分敏感，所以需要使用归一化。

from sklearn.svm import LinearSVC
from sklearn.preprocessing import StandardScaler
from sklearn import datasets
import matplotlib.pyplot as plt
import numpy as np


data = datasets.load_iris()['data']
target = datasets.load_iris()['target']

std = StandardScaler()
std.fit(data)
data = std.transform(data)
data = data[target <= 1][:, :2]# 只取出前两个维度和两个类别
target = target[target <= 1]
svc = LinearSVC(C=1e15)
# sklearn中的C与上面的C一致属于惩罚系数

然后把之前写的ShowBound改一下，改成ShowSvmBound，按照Hard Margin的方式添加两个支持向量

def ShowSvmBound(model, data, target, categories):
    from matplotlib.colors import ListedColormap
    axis = np.array([np.min(data[:, 0]), np.max(data[:, 0]), np.min(data[:, 1]), np.max(data[:, 1])])

    lst = ListedColormap(['#98F5FF', '#54FF9F', '#EEE685'])
    x, y = np.meshgrid(np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) / 0.01)),
                       np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) / 0.01)))
    pre = np.c_[x.ravel(), y.ravel()]

    pre_target = model.predict(pre)
    plt.contourf(x, y, pre_target.reshape(x.shape), alpha=0.5, cmap=lst)
    for i in range(categories):
        plt.scatter(data[target == i][:, 0], data[target == i][:, 1])
    plt.xlim(axis[0], axis[1])
    plt.ylim(axis[2], axis[3])

    w = model.coef_[0]
    b = model.intercept_[0]
    g = (1 - b - w[0] * axis[:2]) / w[1]
    plt.plot(axis[:2], g)
    g = (-1 - b - w[0] * axis[:2]) / w[1]
    plt.plot(axis[:2], g)

然后fit一下SVC，Show一下Bound试一下效果。

from sklearn.svm import LinearSVC
from sklearn.preprocessing import StandardScaler
from sklearn import datasets
import matplotlib.pyplot as plt
import numpy as np


data = datasets.load_iris()['data']
target = datasets.load_iris()['target']

std = StandardScaler()
std.fit(data)
data = std.transform(data)
data = data[target <= 1][:, :2]# 只取出前两个维度和两个类别
target = target[target <= 1]
svc = LinearSVC(C=1e15)
svc.fit(data, target)
ShowSvmBound(svc, data, target, 2)
plt.show()

中间的那一条线就是所求得的超平面，而两边的就是支持向量所在的直线。

核函数

核函数是一种技巧，并不是SVM独有，它的作用是把原本的样本点进行映射，从而使它们从一个空间到另一个新的空间，然后在这个新的空间进行划分。

假设有这么一个数据集，它在样本空间的分布是这样的：

而对于这样的分布，使用一个直线来进行划分就很困难，而使用一个椭圆来进行划分就很简单。
我们使用一种映射，把所有的点都映射到一个新的空间中，即对于所有的原样本空间$R^2$中点$(x^{(1)},x^{(2)})$都给映射到新的样本空间$R^3$变成$(x^{(1{)}^2},2x^{(1)}{x}^{(2)},x^{(2{)}^2})$，在新的空间中记这个坐标为$(z^{(1)},z^{(2)},z^{(3)})$：

此时就可以使用一个平面来进行划分了，假设在原来的$R^2$空间中椭圆的方程是$\frac{x^{(1{)}^2}}{a}+\frac{x^{(2{)}^2}}{b}=1$。把这个椭圆也给映射到$R^3$中得到$\frac{1}{a}{z}^{(1)}+0\cdot z^{(2)}+\frac{1}{b}{z}^{(3)}=1$得到在这种映射规则下椭圆在$R^3$的表达式$\frac{1}{a}{z}^{(1)}+\frac{1}{b}{z}^{(3)}=1$这明显是一个平面的方程，所以我们可以使用支持向量机来进行解决。

观察支持向量机求解$\alpha$的过程
$$\begin{gathered} \underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j({\text{x}}_i\cdot {\text{x}}_j)-\sum _{i=1}^N{\alpha }_i \\ s.t.{\alpha }_i\ge 0(i=1,2...N) \end{gathered}$$
可以发现，最终的结果与样本向量之间的内积有关，而把样本映射到新的空间之后也会改变坐标，假设x经过映射之后变成了$\varphi (x)$那么上述的表达式就会变成
$$\begin{gathered} \underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j[\varphi ({\text{x}}_i)\cdot \varphi ({\text{x}}_j)]-\sum _{i=1}^N{\alpha }_i \\ s.t.{\alpha }_i\ge 0(i=1,2...N) \end{gathered}$$
设函数$K(x,z)=\varphi (x)\cdot \varphi (z)$那么这个K就被称为核函数，核函数就是求经过变换之后的样本在新的样本空间中的内积的函数。

常见核函数

1. 多项式核函数
   
   $$K(x,z)=(x\cdot z+1{)}^p$$
   假设p=2，且只有两个特征则：
   $$\begin{gathered} (x\cdot z+1{)}^2=(x\cdot z{)}^2+2(x\cdot z)+1=(x_1{z}_1+x_2{z}_2{)}^2+2(x_1{z}_1+x_2{z}_2)+1 \\ =x_1^2{z}_1^2+2x_1{z}_1{x}_2{z}_2+x_2^2{z}_2^2+2x_1{z}_1+2x_2{z}_2+1 \\ =(x_1^2,\sqrt{2}{x}_1{x}_2,\sqrt{2}{x}_1,\sqrt{2}{x}_2,1)\cdot (z_1^2,\sqrt{2}{z}_1{z}_2,\sqrt{2}{z}_1,\sqrt{2}{z}_2,1) \end{gathered}$$

于是可以得到$\varphi (x)=(x_1^2,\sqrt{2}{x}_1{x}_2,\sqrt{2}{x}_1,\sqrt{2}{x}_2,1)$而这正是一个二维次多项式的展开式。
2. rbf高斯核函数
$$K(x,z)=e^{-\gamma ||x-z||}$$
其中$\gamma =-\frac{1}{2\sigma }$，根据高斯函数可以知道$\sigma$越小方差越小，换在这里就变成了$\gamma$越小方差越大，而$\gamma$越大方差越小。