算法刷题重温（二）：二叉树的修改构造与递归思维框架（树专题）

1. 写在前面

这篇文章是对二叉树修改和构造方面相关题目的复习， 算是第一篇文章里面某些遍历方式的逆向应用，比如已知某棵树的前序中序遍历，去构造出这棵树来等等。 这篇文章尝试复习三个比较常考的二叉树修改和构造方面题目： 二叉树的镜像或翻转， 构造二叉树和二叉树的序列和反序列化。 通过这三个题目， 可以更好的理解二叉树的遍历思想，也能体会到递归的强大之处，还能培养一种遍历的逆向思维(已知遍历反求树)。 当然，这里不会对这三个题目给出丰富的通俗易懂的思路，因为第一遍的时候我已经整理过，这种东西看LeetCode后面的题解更好， 而我这次的复习主要以共性的东西为主， 形成一种框架思维逻辑，把解题思路由术的层面上升到道。因为我发现， 一种题目确实好的思路解法很多，但我扪心自问了一下， 真正到面试场上，我可能只能写出或回忆一种解法，毕竟我练习的次数和时间有限。 既然只能选择一种，那我愿意选择最能看清题目道层面的那种解法。下面开始复刷这三道题目， 最后也会整理二叉树这块递归思维框架能搞定的一些题目和总结。 这两篇文章把二叉树这块的常考题差不多能走一遍， 后面再遇到了，再进行补充。 开始默写

2. 二叉树的翻转(镜像)

这道题目是Leetcode226. 翻转一棵二叉树， 牛客: 二叉树镜像， 虽然简单，也是各大公司喜欢考的一道题目。通过这道题目再来看一下二叉树的前序和后序遍历， 体验一下第一篇的框架思维。

2.1 前后向遍历的思维

这个题目完全使用二叉树的前向和后向遍历的递归框架即可解决， 只需要修改当前层的处理逻辑。 可以这样想， 给定我当前的root， 我需要交换它的左右子树就OK。 所以核心代码是：

root.left, root.right = root.right, root.left

下面给出前向遍历解决这个问题的代码，直接闭眼先上前向遍历的递归模板，然后修改当前层逻辑：

class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:

        if root == None:
            return
        # 修改当前
        root.left, root.right = root.right, root.left
        
        if root.left:
            self.invertTree(root.left)
        if root.right:
            self.invertTree(root.right)
        
        return root

后向遍历的思路一模一样， 模板+当前层逻辑：

class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:

        if root == None:
            return

        if root.left:
            self.invertTree(root.left)
        if root.right:
            self.invertTree(root.right)
        root.left, root.right = root.right, root.left
        
        return root

2.2 层序遍历的思维

这个题目也可以用层序遍历的模板来解，只需要出栈的时候， 交换出栈节点的左右孩子即可。这个其实不需要锁定每个节点在哪一层上，所以用简洁版的bfs代码即可

from collections import deque
class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:

        if not root:
            return 
        
        # 根节点入队列
        d = deque([root])

        while d:
            # 出队一个元素
            temp = d.popleft()
            # 交换左右子树
            temp.left, temp.right = temp.right, temp.left

            # 左右子树入队列
            if temp.left:
                d.append(temp.left)
            if temp.right:
                d.append(temp.right)
        
        return root

所以通过这个题又发现了之前整理的遍历的几种写法的强大之处， 这个题目中序遍历不行，为啥？ 我们可以想一下， 如果使用中序遍历的时候， 它是先访问左子树， 然后访问根，再访问右子树的逻辑。 这时候，如果我们在访问根的时候交换了左右子树， 那么一梳理这个逻辑， 访问左子树， 交换左右子树， 访问右子树（此时又是左子树了)， 这样有没有发现，始终在左子树上徘徊着？如果真想用中序遍历， 得保证左右子树都能访问着， 所以可以写成这样：

from collections import deque
class Solution:
    # 返回镜像树的根节点
    def Mirror(self, root):
        # write code here
        if root == None:
            return root
        
        if root.left:
            self.Mirror(root.left)
        root.left, root.right = root.right, root.left
        if root.left:
            self.Mirror(root.left)
            
        return root

也就是访问左子树，左右子树交换，再访问左子树， 这时候的左子树正好是右子树，但显然这样不太清晰了。所以中序遍历解这个题目不太好。

3. 二叉树的重建

这个题目是已知二叉树的某向遍历了， 让我们构造二叉树的题目，这属于一种逆向思维， 最常见的就是已知前序和中序遍历，或者后序和中序的遍历来构造二叉树的题目。

• Leecode 105: 从前序和中序遍历构造二叉树
• Leecode 106: 从后序和中序遍历构造二叉树
• 牛客： 重建二叉树： 和上面的一样
• 牛客： 先重建二叉树并输出右视图： 这个既考察了重建， 也考察了层序遍历

虽然是四道题目， 可是核心就是前两道， 通过这两道道题目， 感受一下逆向思维，感受一下递归。

3.1 前序和中序遍历构造二叉树

构造二叉树这里， 直接就思维定势递归+控制下标。 这里的核心是牢牢抓住前序和中序遍历的定义：

• 前序遍历的第一个节点一定是二叉树的根节点，根节点后面的部分， 先是二叉树的左子树部分， 后是二叉树的右子树部分
• 在中序遍历中， 根节点把中序遍历序列分成了两个部分， 左边部分构成了二叉树的根节点的左子树， 右边部分构成了二叉树根节点的右子树

根据上面的思路，就可以把大问题拆开，然后递归。

思路就是我们拿到的是一棵整体的树， 我们需要先从前序遍历里面构造根节点， 也就是第一个元素， 然后去中序遍历序列里面找根节点的位置， 它的左边部分就是左子树， 右边部分就是右子树， 然后我们基于这个范围也可以拿到左子树和右子树的前序序列（因为左子树和右子树的个数前序和中序是一样的， 所以根据中序序列中左右子树的长度就可以定出左右子树的前序序列）。 这样我们就把根据前序和中序序列构造整棵树这个问题拆分成了根据前序和中序序列构造左子树和右子树， 问题就小了， 这很显然， 是个递归构造的过程。

这个题的思路非常清晰， 关键问题是确定好左子树和右子树在前序序列和中序序列的下标范围。所以递归函数里面需要接收的参数有6个， 前序和中序序列（数组）， 然后就是p_start, p_end, i_start, i_end来控制左右子树的下标， 这种题目最好是画个草图：

这里还用到了空间换时间的实现技巧，可以把时间复杂度从$O(n^2)$降到$O(n)$， 原因是我们在前序序列中每个节点， 都需要在中序遍历里面找一遍，锁定位置， 这个是非常耗费时间的， 而我们其实可以通过哈希映射的方式， 用一个数组来存放中序遍历中各个元素的下标位置， 这样我们就不需要每次找了，所以下面给出的代码相对来说是比较优的。这里当时看题解的时候，也有很多简洁版的代码，但这里不整理了，不好实现通解。而我上面这种思路，后序和中序也是同样的方式写即可，好记。下面先梳理逻辑，然后开始默写：

• 这里需要一个辅助函数进行创建， 暂定help函数，该函数作用是根据上面的思路重建二叉树
• help函数里面的逻辑：从先序遍历序列中拿到当前树的根节点，然后到中序遍历中找到该根节点的位置，这样就从中序遍历中划分出了左右子树，然后拿到了左右子树的长度。 然后根据这个长度， 递归的创建根节点的左右子树即可。
• 大函数里面需要做的： 建立一个中序序列的值->位置的映射字典。也记得传入help。

class Solution:
    # 返回构造的TreeNode根节点
    def reConstructBinaryTree(self, pre, tin):
        # write code here
        def help(pre, tin, p_start, p_end, in_start, in_end, hash_map):
            
            # 根据前序遍历建立根节点
            root = TreeNode(pre[p_start])
            
            # 找到根节点在中序遍历的位置
            i = hash_map[root.val]
            # 在中序遍历中计算左右子树的长度
            l_len = i - in_start
            r_len = in_end - i
            
            # 下面递归构建root的左右子树
            if l_len == 0:
                root.left = None
            else:
                root.left = help(pre, tin, p_start+1, p_start+l_len, in_start, in_start+l_len-1, hash_map)
            
            if r_len == 0:
                root.right = None
            else:
                root.right = help(pre, tin, p_end-r_len+1, p_end, in_end-r_len+1, in_end, hash_map)
            
            return root
        
        if not pre:
            return None
        
        # 建立中序遍历值到位置的映射
        hash_map = {
     val: loc for loc, val in enumerate(tin)}
        return help(pre, tin, 0, len(pre)-1, 0, len(tin)-1, hash_map)

3.2 中序和后序遍历构造二叉树

这个和上面的思路一样， 只不过是后序遍历里面最后一个是根节点的位置， 然后每次递归的时候后序序列的下标需要换。 这里的重点依然是把草图画出来，控制好下标即可。

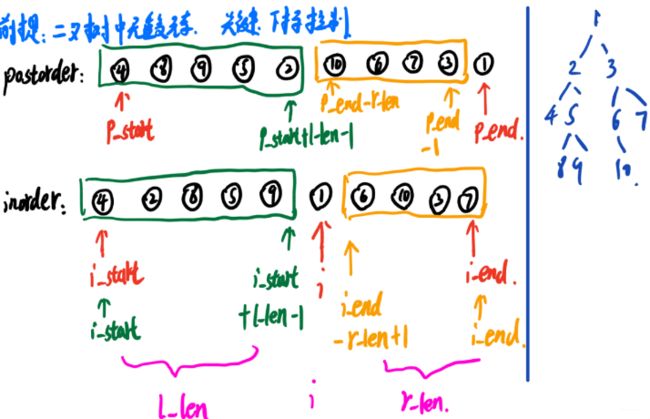
下面直接上代码了， 和上面同样的思路，同样的代码框架即可搞定。

class Solution:
    def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:

        def help(inorder, postorder, in_start, in_end, post_start, post_end, hash_map):

            # 构建根节点
            root = TreeNode(postorder[post_end])

            # 找到根节点在中序遍历中的位置
            i = hash_map[root.val]
            # 计算左右子树的长度
            l_len = i - in_start
            r_len = in_end - i

            # 递归构建左右子树
            if l_len == 0:
                root.left = None
            else:
                root.left = help(inorder, postorder, in_start, in_start+l_len-1, post_start, post_start+l_len-1, hash_map)
            
            if r_len == 0:
                root.right = None
            else:
                root.right = help(inorder, postorder, in_end-r_len+1, in_end, post_end-r_len, post_end-1, hash_map)
            
            return root
        
        if not postorder:
            return None
        
        # 建立映射
        hash_map = {
     val: loc for loc, val in enumerate(inorder)}

        return help(inorder, postorder, 0, len(inorder)-1, 0, len(postorder)-1, hash_map)

有了这两个框架，可以非常轻松的解决上面的四个题目了， 小试一下吧哈哈。这里把第四个题目写了一下，体会了一下模块化的编程：

from collections import deque
class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

class Solution:
    def __init__(self):
        self.res = []
        
    def buildTree(self, pre, tin, p_start, p_end, in_start, in_end, hash_map):
        
        root = TreeNode(pre[p_start])
        i = hash_map[root.val]
        l_len = i - in_start
        r_len = in_end - i
        if l_len == 0:
            root.left = None
        else:
            root.left = self.buildTree(pre, tin, p_start+1, p_start+l_len, in_start, in_start+l_len-1, hash_map)
            
        if r_len == 0:
            root.right = None
        else:
            root.right = self.buildTree(pre, tin, p_end-r_len+1, p_end, in_end-r_len+1, in_end, hash_map)
            
        return root
    
    def findrview(self, root):
        if not root:
            return []
        
        d = deque([root])
        while d:
            size = len(d)
            for i in range(size):
                root = d.popleft()
                if i == size-1:
                    self.res.append(root.val)
                
                if root.left:
                    d.append(root.left)
                if root.right:
                    d.append(root.right)

    def solve(self , xianxu , zhongxu):
        # write code here
        if len(xianxu) == 0:
            return []
        
        # 构建树
        hash_map = {
     val: loc for loc, val in enumerate(zhongxu)}
        root = self.buildTree(xianxu, zhongxu, 0, len(xianxu)-1, 0, len(zhongxu)-1, hash_map)
        
        self.findrview(root)
        return self.res

这种题目感觉比较好，既可以考察建树，又可以考察遍历。

4. 二叉树的序列化与反序列化

这个题目在LeetCode和牛客的Top200高频上见到过：

• Leetcode 297: 二叉树的序列化与反序列化
• 牛客： 序列化二叉树

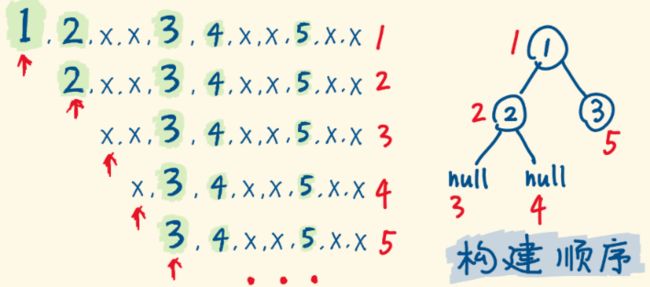
这个题目又把二叉树的遍历和逆向思维整合到了一起， 借助这个题目， 把第一篇里面的遍历和上面的逆序都整合到了一块， 所以借着这个题目，再来温习前中后层遍历以及逆向与递归， 这种题目有没有发现是一种宝题系列哈哈。下面就拿牛客上的这个题来解。先看定义：

这里参考的《lapuladong算法小抄》里面东哥给出的题解思路， 前几天为了刷题，入手了一本，发现太厚了， 很难从头一点点的看完，所以这里提炼了一种框架思维的思想， 然后直接从日常的题目练习中去看这本书，刷到某个专题就重点看里面哪个专题的内容，这样感觉效率会高些。这本书感觉最大的亮点就是培养一种框架式的思维逻辑，然后分门别类的总结题型， 所以正好与我这次刷题的目标一致，跟着前辈学习，确实能节省时间，且人家总结的非常到位，只可惜Java代码居多，我只能学思想哈哈。

4.1 前序遍历的序列与反序列

提到前序遍历， 脑海中应该立即浮现出二叉树的前序遍历递归和非递归模板。然后大体模拟一遍题目的流程采用完成题目的简单的一个。

这道题目显然用递归模板解决序列化问题最合适，因为二叉树的序列化就是将二叉树转成字符串存储，之前我们是转成了列表，这种只需要简单修改递归模板即可搞定。递归逻辑是这样：

• 递归结束条件：如果当前节点空了， 返回’#!’
• 当前层的逻辑： 这个就是得到root.val的字符串形式
• 下一层的逻辑： 序列root的左右子树
• 返回结果： 把cur_val和左右子树的序列化结果保存到字符传中

直接上代码：

	def Serialize(self, root):
        # write code here
        if not root:
            return '#!'
        left_ser = self.Serialize(root.left)
        right_ser = self.Serialize(root.right)
        
        return str(root.val) + '!' + left_ser + right_ser

序列化的结果长这个样子：

如果没有空指针的信息的话， 单单靠前序遍历结果是没法还原二叉树的， 而这里序列化的时候，有空指针信息就好办， 现在接收右边的字符串， 就可以依然采用前序遍历的规则， 先确定root，然后递归生成左右子树。

首先先把字符串转成list， 然后依次弹出list的首项， 用它构建子树的根节点， 顺着list数组， 就会先构建根节点， 构建左子树和右子树。 但是弹出的时候判断一下：

• 如果弹出的字符是’#’， 返回None节点
• 如果弹出的字符不为’#’， 把它当做根节点，然后递归构建左右子树
• 返回： 当前的这棵树

再来个图（来自LeetCode后面的题解）：

直接上代码：

	def buildtree(self, data):
        val = data.pop(0)
        
        if val == '#': return None
        node = TreeNode(int(val))
        node.left = self.buildtree(data)
        node.right = self.buildtree(data)
        return node
    
    def Deserialize(self, s):
        # write code here
        data = s.split('!')
        root = self.buildtree(data)
        return root

3.2 后序遍历的序列与反序列

序列化的操作和前序遍历基本上差不多，只需要把左右子树的结果写前面，最后拼接根

	def Serialize(self, root):
        # write code here
        if not root:
            return '#!'
        left_ser = self.Serialize(root.left)
        right_ser = self.Serialize(root.right)
        return  left_ser + right_ser + str(root.val) + '!'

反序列化操作的时候要注意， 这时候真正根节点应该从尾部开始找了，因为后序遍历的顺序是左 -> 右 -> 根。 那么首先先从尾部找到根， 然后先递归建立右子树， 最后才能是左子树。 所以反序列化的代码长这样了：

	def buildtree(self, data):
        val = data.pop()
        
        if val == '#': return None
        node = TreeNode(int(val))
        node.right = self.buildtree(data)
        node.left = self.buildtree(data)
        return node
    
    def Deserialize(self, s):
        # write code here
        data = s.split('!')
        data.pop()
        root = self.buildtree(data)
        return root

和前序的又是基本上一致， 无非就是建立左右子树的顺序发生了变化。 还要注意就是反函数里面要先data.pop()， 删除末尾的空字符才行。 因为这样的方式序列化的时候， 最末尾会是一个!, 而如果按照这个东西把字符串分开， 最后会有一个空字符。这个是调试中发现的， 一开始提交的时候报错了。

中序遍历在这里不能用， 这个和之前那个翻转还不太一样， 中序遍历序列化好说，但是反序列化的时候找不着根的位置。 因为序列化的时候，这个在两个子树的中间了， 那么反序列化的时候，没办法区分子树中间的哪个值具体是根节点。

3.3 层序遍历的序列与反序列

层序遍历的序列化非常简单，完全层序遍历的简单模板，最后转成字符串即可，当然也不是完全一样， 这里的空指针需要入栈，因为这个我们要进行标识。

def Serialize(self, root):
        # write code here
        if not root:
            return 
        d = deque([root])
        res = []
        while d:
            root = d.popleft()
            if root:
                res.append(str(root.val))
                d.append(root.left)
                d.append(root.right)
            else:
                res.append('#')
        
        return '!'.join(res)

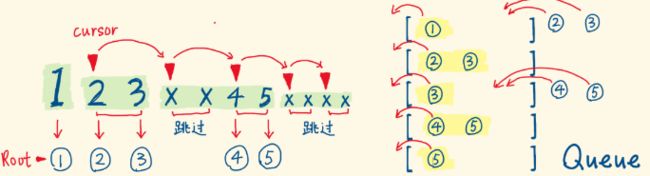
这里反序列化的思想不太好想， 简单了解一下，首先看下序列化之后的结果会是什么样子：

这时候， 我们会发现， 除了第一个节点是根节点的值， 后面的都是成对的，对应左右子节点， 那么我们就可以用个指针从第二项开始扫描， 每次考察两个节点。思路是这样：

• 开始的时候， 根节点值构建根节点， 并让他入队列
• 让节点出队， 考察出列节点， 指针字符指向的字符是它左子节点， 指针右边字符是它右子节点
  • 如果子节点的值不为’#’， 为他创建节点， 并认父亲， 并且要入队列作为未来的父亲
  • 如果子节点的值为’#’， 什么都不做

看下面的图片感受一下：

按照这个思路， 代码如下：

	def Deserialize(self, s):
        # write code here
        if not s:
            return 
        data = s.split('!')
        d = deque([])
        root = TreeNode(int(data.pop(0)))
        d.append(root)
        
        while d:
            node = d.popleft()
            if data:
                val = data.pop(0)
                if val != '#':
                    node.left = TreeNode(int(val))
                    d.append(node.left)
                else:
                    node.left = None
            if data:
                val = data.pop(0)
                if val != '#':
                    node.right = TreeNode(int(val))
                    d.append(node.right)
                else:
                    node.right = None
        return root

5. 从上面的题目中得到递归思维框架

上面这几个题目复习了二叉树的遍历以及其逆向思维， 但是我们还应该看到的是递归的身影， 从术的角度，我们往往是关注于某个问题的具体解法， 而我们这里，尽可能的抽象抽象再抽象， 就可以得到一些道的东西， 而递归的思维框架就是最后可以提炼出的精华，也就是写递归的代码，一定要考虑清楚的问题：

1. 递归终止条件和递归函数的参数设计
2. 递归当前层的逻辑，也就是如何处理当前层
3. 进行递归的逻辑， 探入下一层
4. 考虑是不是需要返回什么结果

所以根据上面的几个问题， 可以得到递归的思维框架：

def recursion(level, param1, param2, ...):
	# recursion terminator
	if level > MAX_LEVEL:
		process_result
		return
	
	# process logic in current level
	process(level, data....)
	
	# drill down
	self.recursion(level+1, p1, ...)
	
	# reverse the current level status if needed

不管是树的各种递归遍历也好，还是逆向构建树也罢，还是什么其他用到递归的问题(分治，回溯也都是基于递归衍生出的小分支)， 只要是涉及到递归的问题，先把这个框架默写出来再说。

下面梳理的二叉树部分递归方面的相关题目， 二叉树的各种深度遍历方式其实就是递归，在第一篇里面已经整理了那些能用遍历框架解决的问题， 这里补充一些不是遍历的框架而单纯用递归的一些题目。

• LeetCode101: 对称二叉树，剑指offer牛客都有: 这个题第一篇里面也整理过， 层序遍历的框架就能搞定， 但递归的思维框架看起来会更加整洁和清晰，标准的递归思维框架， 下一层比较，左子树对应右子树，右子树对应左子树看是否相同
  

• LeetCode100: 相同的树： 这个题目和上面基本上一模一样， 也是标准的递归思维框架，下一层比较的时候，左子树对应左子树，右子树对应右子树，看是否相同
  

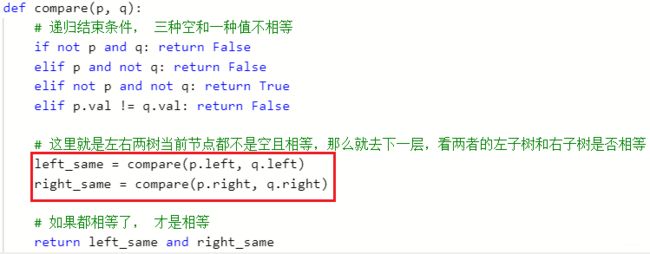
• LeetCode572: 另一个树的子树： 这个题目和上面这两个一样的思路和框架， 但是当前层的逻辑这里， 是需要比较当前的s和t是否相等，也就是用到了上面判断两棵树是否相同的代码。如果当前的s和t不相同， 然后递归去下一层， 看s的左子树是否和t相同， s的右子树是否和t相同， 返回两者的或即可。所以会发现，这些题目的底层思维真的好像。
  

• Leetcode654: 最大二叉树： 前序遍历思想的思维框架， 当前层的逻辑需要找到最大值及其所在位置， 这个题目我学到了下面两点新知识：

  • 类似用数组构造二叉树的题目，每次分隔尽量不要定义新的数组，而是通过下表索引直接在原数组上操作，这样可以节约时间和空间上的开销
  • 如果让空节点（空指针）进入递归，就不加if，如果不让空节点进入递归，就加if限制一下， 终止条件也会相应的调整
    

• Leetcode617: 合并二叉树：
  
  

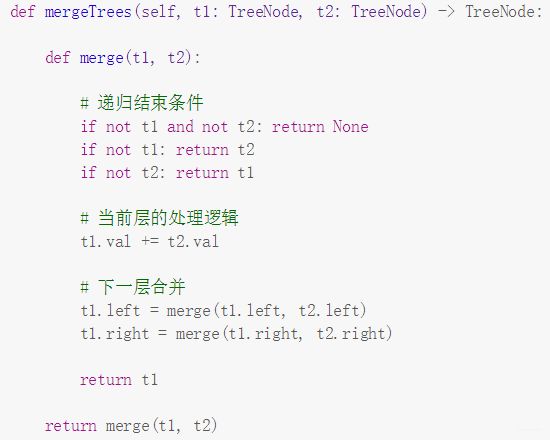
  这里正好借助这个题分析一下递归的四大要素， 这个题开始看题的时候，就想到了递归， 为啥？ 因为有重复子问题， 也就是对于当前的两个根节点， 我进行处理之后， 对于他俩的左子树和右子树，我依然进行同样的合并操作， 也就是重复， 而子问题体现在了左子树和右子树上，也就是树本身的规模会减小。 那么确定了递归之后， 就思维定势直接想四个要素：

  1. 函数参数和递归终止条件： 函数参数好说， 这个就需要合并树，所以只需要拿来两个根节点即可。 递归终止条件就需要考虑两棵树各自为空的情况了， 由于是合并，这里想把t2合并到t1上面， 那么就需要考虑如果当前的t2为空了， 那么就返回t1就行了， 如果当前t1为空了，返回t2，如果都是空了，返回None。 那么不符合上面三种情况，就说明当前的t1和t2都不是空，进行下面的操作。
  2. 当前层的逻辑： 如果当前的t1和t2都不是空， 那么把节点值相加即可
  3. 下一层的逻辑： 当前层处理完， 就去下一层，也就是合并左子树和右子树， 但此时要注意， 合并结果要给到t1才行， 因为这里确实修改了树的结构(我第一次的时候忘了， 结果t2多出来的那部分并没有给到t1), 其实想想上面的递归终止条件里面都有返回的树节点了，也应该这里用树节点接一下结果
  4. 返回值： 这个每一层之后，需要返回t1， 要不然下层合并的结果传不到上面去

  这个题我第一遍写忘了返回值了， 后来才想明白这个问题。

所以通过上面的这些题目，我隐约又感觉出了一点规律， 就是关于递归的返回值和空节点参与递归的考虑：

• 如果只是单纯的遍历查找或者统计这样的， 如果使用前序遍历的思路，一般每一层不需要什么返回值，用全局性的结果统计即可。 而如果是后序遍历的话， 往往会用到返回值，先去左右孩子统计，最后汇总结果用。递归终止条件那里有时候也会看出点东西来。
• 如果是修改树的结构或者是判断树的属性的一些题目，比如对称啊，相同啊等， 这些往往需要返回值，因为修改树的结构，换成各种子问题得把结果汇总到上层去， 而判断树的属性，也往往得把子问题的结果汇报给上层去。
• 然后就是让空节点参与递归，往往会使思路变得更加简单一些， 空节点参不参与递归，会涉及到终止条件的改变

当然上面这几个只是感觉， 感觉性的东西不能全信， 对于解题来讲，依然是底层的思维逻辑才是王道， 感觉只能是辅助，代码的执行过程想清楚才最重要，有时候虽然侥幸能感觉对了， 但其实并不知道程序内部的执行过程，或者由于代码写的非常简洁，不易看清楚执行过程，感觉都不是好事情。 所以现在写代码，不太先追求简洁，先争取逻辑清晰。就比如上面的那些递归， 下一层的那些逻辑其实都可以直接放到返回值里面，但那样反而有时候看不清具体的执行逻辑了，并且python语言本身就可以把代码写的非常简洁，还有一些骚操作， 记得第一遍刷的时候，总是想学学这些东西。 但这一遍通过整理底层的思维框架， 对简洁有了一种新的认识（短不叫简洁)，所以这次会追求一种思维框架清晰且不啰嗦的代码规范。