奈奎斯特稳定性判据的详细推导(手把手教,看完就会!)
奈奎斯特判据的推导:
- 一、幅角原理
-
- 1.s平面到F(s)平面的映射
- 2.F(s)的相角变化
- 3.R = P - Z
- 二、复变函数F(s)的选择
-
- 1.如何选择F(s)才能与系统稳定性结合
- 2. 1+G(s)H(s) 的优点
- 3. 1+G(s)H(s) 和 G(s)H(s) 的关系
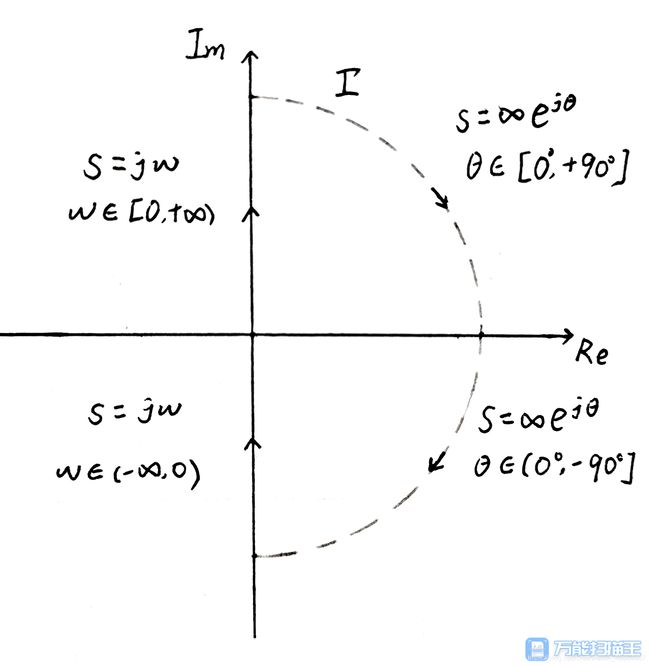
- 三、闭合曲线 Γ 的选择
-
- 1. G(s)H(s) 无虚轴上的极点
- 2. G(s)H(s) 有虚轴上的极点
- 四、R的求取
-
- 1.已知曲线 Γ 如何绘制半闭合曲线 ΓGH ?
-
- ①G(s)H(s) 无虚轴上的极点
- ②G(s)H(s) 有虚轴上的极点
-
- 1、极点在原点
- 2、极点在虚轴两侧
- 2.R = 2(N+ - N-)
- 五、判断系统稳定性
- 六、总结
提示:本文是奈奎斯特判据的详细推导,能够透彻的了解其中的原理,如果你想快速了解该判据的步骤,可参考我的另一篇文章,链接见文末
一、幅角原理
1.s平面到F(s)平面的映射
设s为复数变量F(s)为s的有理分式。对于s平面上的任意一点,通过F(s)的映射关系,在F(s)平面上必然可确定关于s的象
在s平面上任选一条闭合曲线 Γ ,且不通过F(s)的任一零、极点。当s从闭合曲线 Γ 上任意一点A顺时针沿曲线 Γ 运动一周后,相应地F(s)在F(s)平面上也从F(A)点形成一条闭合曲线 ΓF
即 s的取值为闭合曲线 Γ 上的无数个点,通过F(s)的运算得到无数个新的点,将这些新点连接就是我们的 ΓF
举一个很简单的例子: F ( s ) = 3 s F(s) = 3s F(s)=3s在s平面上取闭合曲线 Γ 为 |Z| = 1 的圆,如图,经过映射之后在F(s)平面得到的图形为 |Z| = 3 的圆

2.F(s)的相角变化
先问一个问题:当s从闭合曲线 Γ 上任意一点顺时针沿 Γ 运动一周后,F(s)的相角变化了多少?
我们以一个简单的传递函数为例: F ( s ) = s − ( 2 + 2 j ) \text{}F\left( s \right) =s-\left( 2+2j \right) \ \ \text{} F(s)=s−(2+2j) 其中传递函数的零点为 z = 2 + 2j,F(s)的相角变化就是 ∠s - z 积累的角度,以下根据闭环曲线 Γ 与零点Z的关系分成两种情况讨论
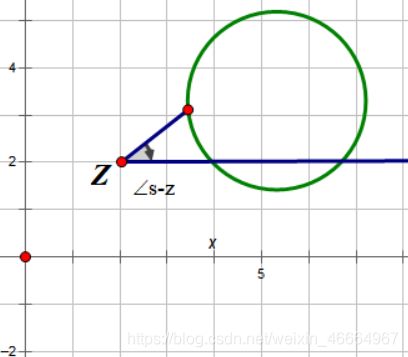
①若选取的闭环曲线 Γ 未包含 z = 2 + 2j ,那么随着点s在闭环曲线上运动一周,我们以z为原点建立坐标系,发现 ∠s - z 最后没有积累角度,F(s)的相角变化为0 :
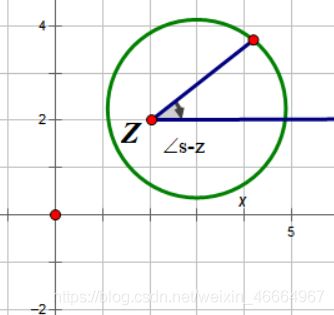
②若选取的闭环曲线 Γ 包含 z = 2 + 2j ,那么随着点s在闭环曲线上运动一周,s回到了原来位置上,但此时 ∠s - z 顺时针积累了2π的角度,F(s)的 相角变化为2π:
所以我们得到结论:
对于闭合曲线 Γ 外的零点和极点,对应的相角变化为0
对于闭合曲线 Γ 内的零点和极点,对应的相角变化为2π
注:闭合曲线 Γ 不通过F(s)的任一零、极点。F(s)的零、极点要么在曲线里面,要么在曲线外面
3.R = P - Z
问一个问题:当传递函数同时有零点、极点,如何分析F(s)的相角变化? 令 : F ( s ) = ( s − z 1 ) ( s − z 2 ) ( s − p 1 ) ( s − p 2 ) 令:F\left( s \right) =\frac{\left( s-z_1 \right) \left( s-z_2 \right)}{\left( s-p_1 \right) \left( s-p_2 \right)} 令:F(s)=(s−p1)(s−p2)(s−z1)(s−z2)F(s)可以化为 A z 1 A z 2 A p 1 A p 2 e ( φ z 1 + φ z 2 − ( φ p 1 + φ p 2 ) ) \frac{A_{z_1}A_{z_2}}{A_{p_1}A_{p_2}}e^{\left( \varphi ^{z_1}+\varphi ^{z_2}-\left( \varphi ^{p_1}+\varphi ^{p_2} \right) \right)} Ap1Ap2Az1Az2e(φz1+φz2−(φp1+φp2))
于是我们可以得到F(s)的相角变化 δ ∠ F ( s ) = δ ∠ s − z 1 + δ ∠ s − z 2 − δ ∠ s − p 1 − δ ∠ s − p 2 \delta ∠F\left( s \right) =\delta ∠s-z_1+\delta ∠s-z_2-\delta ∠s-p_1-\delta ∠s-p_2 δ∠F(s)=δ∠s−z1+δ∠s−z2−δ∠s−p1−δ∠s−p2极点p1、p2作为分母,与零点z1、z2产生的相角变化相反
幅角原理:
F(s)绕平面原点的圈数只和F(s)被闭合曲线 Γ 包围F(s)的零点和极点的代数和有关
设F(s)有Z个零点和P个极点被 Γ 包围,则s沿曲线 Γ 顺时针运动一周时,F(s)变化的相角为 2π(P - Z),在F(s)平面上,闭合曲线 ΓF 逆时针包围原点的圈数为 R = P − Z R = P - Z R=P−Z▷R: ΓF 逆时针包围原点的圈数
▷P:F(s)在s平面闭合曲线 Γ 内被包围的极点数
▷Z:F(s)在s平面闭合曲线 Γ 内被包围的零点数
R > 0 和 R < 0分别表示 曲线ΓF 逆时针包围原点和顺时针包围原点的圈数,R = 0 表示曲线 ΓF 不包围原点
为什么是 ΓF 包围原点的圈数,而不是其它点呢?
因为我们计算得到F(s)相角的变化为2π的整数倍,在F(s)平面中,要使F(s)对应的点变化的相角为2π的整数倍,那么闭合曲线 ΓF 里一定要包含原点,所以我们取包含原点的圈数
如何将幅角原理与系统稳定性结合起来呢?别着急我们慢慢往下看
二、复变函数F(s)的选择
1.如何选择F(s)才能与系统稳定性结合
☆ F(s)选择成: 1 + G ( s ) H ( s ) 1+G(s)H(s) 1+G(s)H(s)为什么?1+G(s)H(s)有什么特殊意义吗?
对于这样一个负反馈系统:
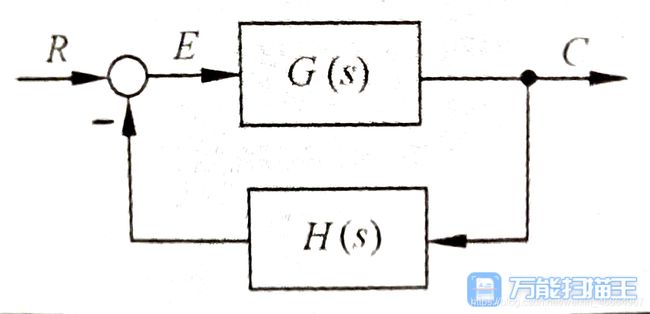
令 : G ( s ) = s + 2 s + 5 , H ( s ) = 1 s + 4 令:G\left( s \right) =\frac{s+2}{s+5}\ \ ,H\left( s \right) =\frac{1}{s+4} 令:G(s)=s+5s+2 ,H(s)=s+41可以得到:

发现1+G(s)H(s)的分子分母具有特殊的意义:
▷1+G(s)H(s)的零点为闭环传递函数的极点
▷1+G(s)H(s)的极点为开环传递函数的极点
那么使用1+G(s)H(s)就可以同时包含开环传函和闭环传函的极点
2. 1+G(s)H(s) 的优点
在控制系统中是利用开环传递函数来判断闭环系统的稳定性的
若我们将s平面的闭合曲线 Γ 取成整个右半平面
那么对于F(s)=1+G(s)H(s)来说,我们令F(s)在右半平面的零点数和极点数为 Z 和 P
右半平面中闭环传递函数的极点数为0,则系统稳定,即Z = 0 系统稳定
F(s)的极点为开环传递函数的极点,开环传函是已知的,即 P是已知的
在F(s)平面中,闭合曲线 ΓF 逆时针包围原点的圈数为:
R = P − Z R = P - Z R=P−Z
至此,P、Z的意义转化为:
▷R: ΓF 逆时针包围原点的圈数
▷P:开环传递函数在右半平面内的极点数,P是已知的
▷Z:闭环传递函数在右半平面内的极点数,若Z = 0 系统稳定
注意:转化的前提是 ① Γ 取成整个右半平面 ②F(s)=1+G(s)H(s)
至此我们只要结合幅角原理判断Z是否为0,即可判断系统是否稳定了
3. 1+G(s)H(s) 和 G(s)H(s) 的关系
ΓF 与 ΓGH 的关系
F(s)=1+G(s)H(s),相当于在G(s)H(s)的实部加1,即G(s)H(s)向实轴正方向平移了1个单位得到了F(s)
G(s)H(s)对应的闭合曲线 ΓGH 向右平移一个单位得到 F(s) 对应的闭合曲线 ΓF
则R等于 ΓGH 逆时针包围F(s)平面上 点 (-1 , j0) 的圈数
为什么要进行这个等价呢?
因为开环传递函数 G(s)H(s) 比 F(s) 更加有利于分析
至此还剩下两个问题:
①如何设计闭合曲线 Γ ,使得能取满整个右半平面?
②P是已知的,如何求得R?
三、闭合曲线 Γ 的选择
如何设计闭合曲线 Γ ,使得能取满整个右半平面?
幅角原理中要求闭合曲线 Γ 不通过 F(s)的任一零、极点,则 Γ 的选择与虚轴上有无零极点有关
为什么这里一会儿用G(s)H(s) ,一会儿又用 F(s)呢?为什么不考虑虚轴上零点的情况呢?
因为 F(s) = 1+G(s)H(s)的极点 P 就是 G(s)H(s) 的极点,而 F(s) 的零点 Z 是要求解的量,所以讨论G(s)H(s)极点的位置即可
1. G(s)H(s) 无虚轴上的极点
2. G(s)H(s) 有虚轴上的极点
若虚轴上有极点,为了避免闭合曲线 Γ 通过零、极点,我们可以想办法绕过去,则画一个半径无穷小的半圆绕过极点,我们这里只讨论极点在原点的情况:
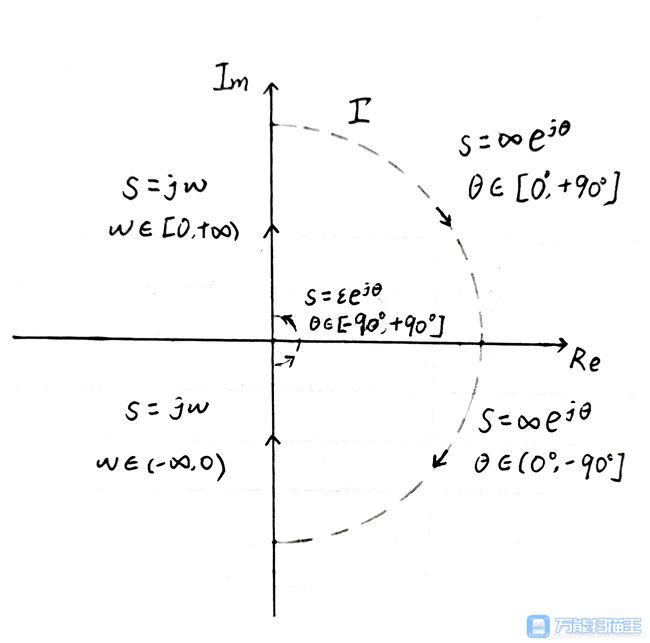
四、R的求取
R等于 ΓGH 逆时针包围F(s)平面 点(-1 , j0) 的圈数,那么我们将 ΓGH 画出来就可以计算R的大小了
在绘制曲线之前我们先解决两个问题:
①为什么要绘制 G(s)H(s) 闭合曲线 ΓGH ,而不是 ΓF ?
因为选取的s平面闭合曲线 Γ 关于实轴对称, G(s)H(s)是实系数有理分式函数,所以闭合曲线 ΓGH 关于实轴对称。所以我们只用画出 ΓGH 的一半,即Im(s) > 0,s ∈ Γ对应的闭合曲线,这里我们把它叫做半闭合曲线 ΓGH
②为什么闭合曲线 ΓGH 关于实轴对称?
首先 Γ 关于实轴对称,且G(s)H(s)是实系数有理分式函数,意思在表达式里只含有实数,我们举一个例子: G ( s ) H ( s ) = s + 1 s − 3 G(s)H(s)=\frac{s+1}{s-3} G(s)H(s)=s−3s+1取关于实轴对称的两点(2+2j)、(2-2j),代入传函得到: 3 + 2 j − 1 + 2 j 、 3 − 2 j − 1 − 2 j \frac{3+2j}{-1+2j}\ \ \text{、\ }\frac{3-2j}{-1-2j} −1+2j3+2j 、 −1−2j3−2j很明显二者幅值相同,相角相反,关于实轴对称。
1.已知曲线 Γ 如何绘制半闭合曲线 ΓGH ?
①G(s)H(s) 无虚轴上的极点
s = j w , w ϵ [ 0 , + ∞ ) , 即虚轴正半轴 s=jw,w\epsilon \left[ 0,+\infty \right) ,\text{即虚轴正半轴} s=jw,wϵ[0,+∞),即虚轴正半轴
将s = jw 代入开环传递函数G(s)H(s),发现这就是开环奈奎斯特曲线!
(2)
s = ∞ e j θ , θ ϵ ( 90 ° , 0 ° ] ,即第一象限 1 4 圆弧 s=\infty e^{j\theta},\theta \epsilon \left( 90°,0° \right] \text{,即第一象限}\frac{1}{4}\text{圆弧} s=∞ejθ,θϵ(90°,0°],即第一象限41圆弧
代入开环传递函数G(s)H(s)得
K ( ∞ e j θ ) m + ( ∞ e j θ ) m − 1 + … … ( ∞ e j θ ) n + ( ∞ e j θ ) n − 1 + … … \frac{K\left( \infty e^{j\theta} \right) ^m+\left( \infty e^{j\theta} \right) ^{m-1}+……}{\left( \infty e^{j\theta} \right) ^n+\left( \infty e^{j\theta} \right) ^{n-1}+……} (∞ejθ)n+(∞ejθ)n−1+……K(∞ejθ)m+(∞ejθ)m−1+……
若n > m,计算结果为平面原点
若n = m,计算结果为系统的增益K
综上,得到对应的闭环曲线为一个点,这个点就是开环奈奎斯特曲线的终点!
所以当G(s)H(s) 无虚轴上的极点时,半闭合曲线 ΓGH 就是开环奈奎斯特曲线 !! ,是不是突然就有迹可循了
关于奈奎斯特曲线的绘制,可以参考我的这篇文章
▷ 三种绘制奈奎斯特曲线的方法
②G(s)H(s) 有虚轴上的极点
1、极点在原点
s = j w , w ϵ [ 0 , + ∞ ) ; s = ∞ e j θ , θ ϵ [ + 90 ° , 0 ° ] s=jw,w\epsilon \left[ 0,+\infty \right) \text{;}s=\infty e^{j\theta},\theta \epsilon \left[ +90°,0° \right] s=jw,wϵ[0,+∞);s=∞ejθ,θϵ[+90°,0°]
对应的就是开环奈奎斯特曲线
(2)当
s = ε e j θ , θ ϵ [ 0 ° , 90 ° ) ,即第一象限 1 4 小圆弧 s=\varepsilon e^{j\theta},\theta \epsilon \left[ 0°,90° \right) \text{,即第一象限}\frac{1}{4}\text{小圆弧} s=εejθ,θϵ[0°,90°),即第一象限41小圆弧
发现这一段圆弧的末尾就是 s=jw ,而 s=jw 是开环奈奎斯特曲线的起点,所以小圆弧对应的半闭合曲线的终点 就是开环奈奎斯特曲线的起点
以 G ( s ) H ( s ) = 1 s v ( s + 1 ) 为例 \text{以\\ }G\left( s \right) H\left( s \right) =\frac{1}{s^v\left( s+1 \right)}\ \ \text{为例} 以 G(s)H(s)=sv(s+1)1 为例
代入 s = ε e j θ ( ε → 0 + ) , θ ϵ [ 0 ° , + 90 ° ] 得 \text{代入}s=\varepsilon e^{j\theta}\left( \varepsilon →0^+ \right) ,\theta \epsilon \left[ 0°,+90° \right] \text{得} 代入s=εejθ(ε→0+),θϵ[0°,+90°]得
G ( s ) H ( s ) = 1 ε v e j v θ ⋅ G 1 ( ε e j θ ) G\left( s \right) H\left( s \right) =\frac{1}{\varepsilon ^ve^{jv\theta}}\cdot G_1\left( \varepsilon e^{j\theta} \right) G(s)H(s)=εvejvθ1⋅G1(εejθ)
A ( 0 + ) = ∞ A\left( 0^+ \right) =\infty A(0+)=∞
φ ( 0 + ) = ∠ v × ( − 90 ° ) + ∠ G 1 ( j 0 + ) \varphi \left( 0^+ \right) =∠v\times \left( -90° \right) +∠G_1\left( j0^+ \right) φ(0+)=∠v×(−90°)+∠G1(j0+)
观察 A 和 φ ,发现对应的半闭合曲线是一个 半径无穷大,弧度为∠v×(-90°)的圆弧,但它的起点未知
但是,我们知道对应曲线的终点就是奈奎斯特曲线的起点
所以我们以奈奎斯特曲线的起点 逆时针做一个半径无穷大、弧度为∠v×(-90°) 的圆弧
所以 当G(s)H(s) 有虚轴上的极点,且为积分环节 时
半闭合曲线 ΓGH 为 开环奈奎斯特曲线加上一个半径无穷大、弧度为∠v×(-90°) 的圆弧
举例:其中 v = 2
![]()
注:逆时针作一个∠v×(90°) 的圆弧,但圆弧的方向是顺时针,因为角度为负数
2、极点在虚轴两侧
即开环传函有等幅振荡环节
G ( s ) H ( s ) = 1 ( s 2 + w n 2 ) v G 1 ( s ) G\left( s \right) H\left( s \right) =\frac{1}{\left( s^2+w_n^2 \right) ^v}G_1\left( s \right) G(s)H(s)=(s2+wn2)v1G1(s)
这里就不进行证明了,直接得出结论:
当G(s)H(s) 有虚轴上的极点,且含有等幅振荡环节时
半闭合曲线 ΓGH 为 开环奈奎斯特曲线加上一个半径无穷大、弧度为∠v×(-180°) 的圆弧
同样,圆弧的终点为奈奎斯特曲线的起点,方向为顺时针
2.R = 2(N+ - N-)
通过上面的过程,绘制出了系统的半闭合曲线 ΓGH ,R是闭合曲线逆时针绕 (-1,j0) 的圈数,N+为 (-1,j0) 左侧 正穿越 的次数 (从上往下) ,N-为 (-1,j0) 左侧 负穿越 的次数 (从下往上),通过几何关系得到
R = 2 ( N + − N − ) R = 2(N_+ - N_-) R=2(N+−N−)
半闭合曲线 ΓGH 只有闭合曲线 ΓGH 关于实轴对称的一半
五、判断系统稳定性
Z = P - R Z = P-R Z=P-R
通过以上的步骤,我们通过画图、计算得到了R,又P是已知的,那么Z就可以计算出来了
Z是闭环传递函数在右半平面的极点数
若Z = 0 ,则系统稳定,反正系统不稳定
六、总结
我们再重新捋一遍思路
①整个推导的核心:
R ( 作 图 求 得 ) = P ( 已 知 量 ) - Z ( 希 望 为 0 ) R (作图求得)=P(已知量)- Z(希望为0) R(作图求得)=P(已知量)-Z(希望为0)
结合幅角原理和F(s)=1+G(s)H(s) 的性质,并取 Γ 为整个右半平面,使得R、P、Z有以下含义:
▷R: ΓF 逆时针包围原点的圈数
▷P:开环传递函数在右半平面内的极点数
▷Z:闭环传递函数在右半平面内的极点数
R同时等于ΓGH 逆时针包围F(s)平面上 点 (-1 , j0) 的圈数
因为在控制系统中是利用开环传递函数来判断闭环系统的稳定性的,开环传递函数是已知的,所以右半平面的极点P已知
②半闭合曲线的绘制
(1)若无虚轴上极点,则绘制奈奎斯特曲线
(2)若极点在原点处,含有积分环节,则绘制开环奈奎斯特曲线加上一个半径无穷大、弧度为∠v×(-90°) 的圆弧
(3)若极点在虚轴两侧,含有振荡环节,则绘制开环奈奎斯特曲线加上一个半径无穷大、弧度为∠v×(-180°) 的圆弧
③求解R
R = 2 ( N + − N − ) R = 2(N_+ - N_-) R=2(N+−N−)
N+为半闭合曲线 ΓGH 在 (-1,j0) 左侧 正穿越 的次数 (从上往下) ,N-为 (-1,j0) 左侧 负穿越的次数 (从下往上)
④求解Z
Z = P - R Z = P-R Z=P-R
若Z = 0 则系统稳定,反之系统不稳定
以上是本人关于奈奎斯特判据的体会,若有错误,欢迎大家批评和交流(*^▽ ^*)/若想要再巩固奈奎斯特判据的步骤,可参考我的这篇文章:
▷奈奎斯特稳定性判据的步骤